圏論的集合論である ETCS における集合と写像の定義

ETCS -- ETCS の簡単な解説 (nLab 記事)
fully formal ETCS -- ETCS の一階の言語による具体的な形式化方法などの ETCS に関するより踏み込んだ解説 (nLab 記事)
An elementary theory of the category of sets (long version) with commentary -- ETCS 考案者であるウィリアム・ローヴェア (William Lawvere) 自身が書いた論文

ここでの説明も、基本的にはソーンダース・マックレーン (Saunders Mac Lane) の著書「圏論の基礎」の付録として掲載されている「圏論の数学的基礎論への応用」の話をできるだけわかりやすくなるようにかみ砕いたものとなっている。

一応注意喚起しておくと、上に貼った「fully formal ETCS」からの引用になるが、

This page addresses a frequently voiced but easily corrected misconception about categorial approaches to foundations of mathematics, namely that there is a logical circularity in using category theory to give an axiomatic set theory (such as ETCS), since categories themselves are sets (or collections) with extra structure.

というように、残念ながら「ETCS は定義が循環している」という誤解は ("frequently voiced" と書かれているくらいには) ありふれたことという立ち位置にある。

つまり数学者等に ETCS の是非を伺った場合、(相手が圏論徒でもない限り) 直ちに否定される可能性が高いということは最低限覚悟しておいた方が良いかもしれない。

写像と集合

定義

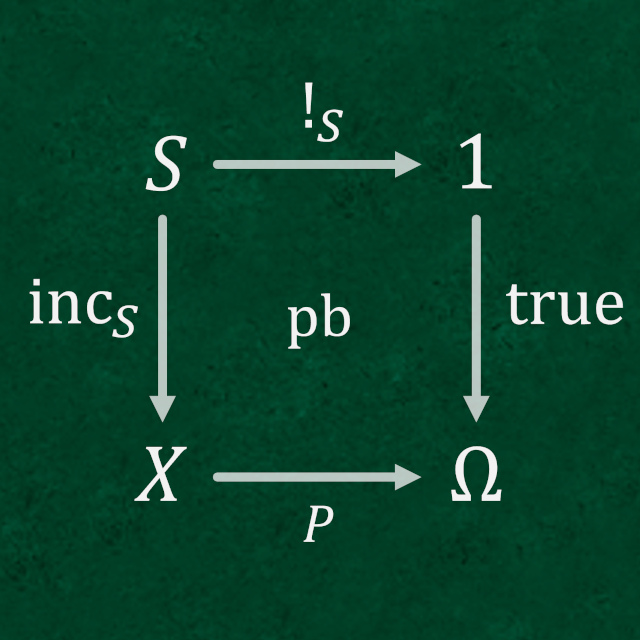
以下に示す性質 (詳細については後述) を全て満たす特別な種類の圏について、その種の圏の射を写像 (mapping) あるいは関数 (function) などと呼ぶ。また、そのうち対象 (圏の持つノード) のことを集合 (set) あるいは「従来の集合の概念」と区別して抽象集合 (abstract set) などと呼ぶ。一方で、従来の「各々の要素が、属している集合とは独立に形あるものとして存在可能な集合」のことを具体集合 (concrete set) と呼ぶこともある。

トポスである
自然数対象を持つ
Well-pointed である
選択公理を満たす

以上の圏の性質一式は ETCS (Lawvere's Elementary Theory of the Category of Sets) 公理系といい、その公理を満たす圏の一般論は ETCS 集合論と呼ばれる。(ETCS はしばしば「集合の圏の初等理論」と直訳される。)

注意してほしいのは、ETCS "集合論" とは謳われているものの、素朴集合論や ZFC, NBG といった従来の公理的集合論のようなものを期待してはいけない。ETCS は構造的集合論 (structural set theory) と呼ばれる種類の集合論であり、そういった従来の物質的集合論 (material set theory) と呼ばれる種類の集合論とは趣がだいぶ異なる。

具体的にどのように異なるのかは以下を参考にしてほしい。

structural set theory (nLab 記事)
material set theory (nLab 記事)

(「構造的集合論」や「物質的集合論」という日本語訳は単に直訳しただけで、恐らく正式なものではない。)

余談

より一般に、抽象集合という言葉は「トポスの対象」のことを指す言葉として使われる場合が多い。また特別な種類の抽象集合として「well-pointed トポスの対象」のことを定抽象集合 (constant abstract set) と呼ぶこともある。

ちなみに写像 \(f:X\rightarrow Y\) について

ドメイン \(X\) は写像 \(f\) の定義域
コドメイン \(Y\) は写像 \(f\) の終域または行き先

などと呼ばれる。

余談

見ての通りここで採用している公理化の下では集合は厳密に写像の括りの中に置かれるため、集合を写像として "扱う" ことを避けることはできないが、この見方はホモトピー型理論の視点からは不自然に映るため、直接的に集合を写像と "呼ぶ" ことはできる限り控えていく方針をとる。

注意点

写像は集合ではない

ZFC のような集合論では、写像は集合として見做されるが、ETCS 集合論では、写像と集合の立ち位置がちょうど真逆になる。

つまりは、ZFCでは「写像は集合の括りの中に置かれる」が ETCS では「集合が写像の括りの中に置かれる」ということである。

例えば「集合」側に着目する ZFC では、

ある "集まり" は、ZFC 公理系によって定義される一つの集合として構成できるのか？

という視点になるが、ETCS では

「ある "対応の規則の情報を付随する記号 (の実体)" は、ETCS 公理系を満たす圏の一つの射として構成できるのか」

というように、「写像」側が厳密に構成可能であるのかを気を付ける必要性が生じてくる。

それから ZFC からの視点だと、積集合や逆像といった「複雑な集合構成を持つ集合」が公理的に定義される ETCS に対して「トップダウン」という印象を抱きがちだが、これは

ETCS では写像の構成を公理から演繹的に行わなければならない

という点を見失っていて、実際は ZFC と同等かそれ以上に「ボトムアップ」なアプローチをとる必要がある。

因みにこの「ETCS は実はボトムアップである」というのは僕の独断的な印象というわけでもなく、例えば

Trimble on ETCS III (nLab 記事)

の記事から言葉を引用すると

So: with ZFC it’s more as if you can just hop in the car and go; with ETCS you build the car engine from smaller parts with your bare hands, but in the process you become an expert mechanic, and are not so rigidly attached to a particular make and model ( e.g., much of the theory is built just on the axioms of a topos, which allows a lot more semantic leeway than one has with ZF).

というように形容する人もいる。

また、ZFC と ETCS の具体的な違いについては、著名な Michael Shulman が作った以下のスライドにわかりやすくまとまっているので是非読んでみてほしい。

Complementary foundations for mathematics: when do we choose? (PDF)

ETCS 集合論は ZFC 集合論よりも弱い

既に何度も言っていると思うが、ETCS では「置換公理型 (axiom schema of replacement)」が標準では含まれない。

つまりは、ETCS の対比として ZFC を挙げるのは厳密にはあまり適切とは言えず、フェアに考えるのであれば、ZFC から置換公理型を除いた「ZFC - Replacement」が ETCS と肩を並べる集合論に該当するだろう。

詳しく知らない分野の話になるけど、実際 nLab 曰く、「Borel determinacy が真であるか」という問題は ZFC では証明可能だが、ETCS からは証明できないとのこと。一方で、ETCS に置換公理型を加えた「ETCS + R」という集合論ではそれが証明できるらしい。(この種の話にはそこまで興味がなく、今後もこういった話に関する記事を僕のこのサイトで書く予定はないので、詳しく知りたい人は各自調べてほしい。)

ドメインやコドメインを写像から切り離すことは不可能

圏の公理より、任意の射は固有のドメインやコドメインを持たなければならず、写像が圏の射として定義される以上は、写像とそのドメイン・コドメインとが不可分な概念として扱われることが不可避となる。

従来の写像のグラフによる写像や関数の定義では、写像のコドメインはオプション的な立ち位置にある別段明示的に与えられている必要のないものと捉えることもできる一方で、ETCS 集合論的な写像の定義においては、ドメインはもちろんコドメインも写像から切り離して考えることは技術的に不可能となる。

この事をちょっとした簡単な記事にもまとめてみたので、以下参考になれば。

写像に終域は必要ない？

集合は単なる圏の中のノード

圏の定義から明らかなように、圏の対象は具体的なデータなんてものを一切保有しておらず、「圏の中の一点」以上の意味はない。もちろん「特定の性質を満たす圏の対象」という形で定義されている抽象集合という概念も例外ではなく、結局は点でしかない。しかし逆にいえば「どのノードであるのか」を指定することさえできれば、具体的に抽象集合が定まったことを意味する。(「漠然とした点」として捉えたのでは、確かに点同士の間の意味の違いはもちろん見出せない。一方「圏の中の点」として見た場合、点の周りに張られている矢印のネットワークを解析することで、点への意味付けが実現することになる。ノード周りにどういった矢印が配置されているのかは、考えるノードに依るため、結果として点同士の間での意味の違いが明確に見えてくるようになる。)

集合の要素は圏の住人として存在している

先ほど「集合は単なる圏の中のノード」であることを強調したが、かといって集合の要素を取り扱えないわけではない。
幸いにも ETCS 公理系を満たす圏は「カルテシアン閉圏」であるため、終対象からの射として対象の要素を取り扱うことができる。

(集合の要素たちは大域要素関係 \(\in(x,y)\) を介した属している集合への紐づけがされていないものの、それらはしっかりと圏の中には存在している。また大域要素関係による紐づけがされていないとはいっても、圏の公理より射からドメイン・コドメインは切り離せないため、どの集合の要素であるのかを見失う心配はない。 -- 写像がコドメインを持つからこそ、こういった捉え方が可能になる。)

例えば

\(1:1\rightarrow 1\)
\({\rm inj}_1:1\rightarrow 1+1\)
\({\rm inj}_2:1\rightarrow 1+1\)
\({\rm zero}:1\rightarrow {\mathbb{N}}\)
\(({{\rm zero} {\sf \, ⨟ \,} {\rm succ}}):1\rightarrow {\mathbb{N}}\)
\(\langle {\rm zero}, {\rm zero} \rangle:1\rightarrow {\mathbb{N}}\times{\mathbb{N}}\)
\({\rm arrToEl}({\rm succ}):1\rightarrow {\mathbb{N}}^{\mathbb{N}}\)
\({\rm true}:1\rightarrow \Omega\)
\(({\rm arrToEl}(\Omega) {\sf \, ⨟ \,} (\forall_{\Omega})):1\rightarrow \Omega\)

集合と集合の要素への意味づけは分けて考える必要がある

例えば、ZFC 集合論では

\[ f:\{2\}\rightarrow X \]

といった形の写像の定義がしばしば行われるが、ETCS 集合論においては、「集合それ自体が自身の要素に対して固有の意味を与えない」という事実からわかるように、そのような記述は通常行われない。

強いて言えば、 \(\{2\}\) という記号を

要素への意味付けを行う射 \(1\rightarrow {\mathbb{N}}\) として \({\rm zero}{\sf \, ⨟ \,}{\rm succ}{\sf \, ⨟ \,}{\rm succ}\) が指定された集合 \(1\)

として定義すれば ETCS 集合論でもそのような記述ができないこともないが、\(f\) を定義するうえで、要素の意味を指定するための付加構造の存在を明示する必要性は基本的になく、敢えてそのようなノイズとなる情報を数式上に表示させるのは好ましくないかもしれない。

従来の変数を用いた写像の定義ができることは自明ではない

繰り返しになるが、写像と聞くと

\[ f(x) = ... \]

といったように値の対応の規則 (記号操作のルール) を指定することで定義できるものと考えたくなるかもしれない一方、ETCS 集合論では、写像は「射 (具体的な実体あるモノ)」であり、そういった記号列を宣言したところで、写像が何処からともなく舞い降りてくるといった奇跡が起こることは公理的に保証されているわけではない。

特に ETCS 公理系には「置換公理型」「分出公理型」は含まれないため、ZFC のように「変数を含む論理式」を直接的に集合の構成に使用することは基本的にできない。

(..)

例えば圏 \((\cdot \rightrightarrows \cdot)\) について (\(f,g:X\rightarrow Y\) をその圏の持つ非自明な射としたとき)

\[ h(x) = ... \]

という形のおまじないによって、非自明な平行な2つの矢印 \(f,g\) の参照が機能するのか否かを考えてみれば容易に気付けるだろう。
対象 \(X\) の非自明な一般化要素が圏の中に存在しないため、要素をもとに矢印 \(f,g\) の違いを判別することがまずできない。

ETCS 公理系を満たす圏というのも例外ではなく、写像は「圏の中で発見 (discover) することが可能な矢印」というポジションであることには変わりない。(well-pointed 公理というのも、既に発見済みの2つの平行な矢印に対する相等関係に関する言明であり、ZFC の外延性公理と同様、新たな矢印の存在を導くことに繋がる公理ではない) つまり構文的に定義した風を装っただけのフワフワした宙ぶらりんなナニカを写像として無造作に理論の中に持ち込むことは、ETCS 集合論的には基本的に許されない。

それ故、「\(f(x)=...\) によって定義される写像」ではなく「\(f(x)=...\) を満たす写像 (そのような関係式を満たす写像が実際に圏の中に存在するかどうかは別問題としてしっかり調べる必要がある。ちなみに存在すれば well-pointed 公理よりその条件を満たす射の一意性は保証される)」という言い回しを使用する

またしばしば圏論的集合論に対して、「一階の言語で写像に対する全称量化子や存在量化子を考えることは許されないのでは」と思われてしまうが、上記の説明を読めばこれが誤解であることに容易に気付けるだろう。(そもそも射を写像として見做すことができるのは後付けであり、そのもととなっている射の実体は何度も言うように単なる矢印でしかない。)

より具体的なことは「関数のパターンマッチング f(x) = [...] による関数の圏論的構成法」にまとめている。

ETCS 公理系の一階の言語による記述

圏の公理

(...)

終対象の存在公理

(...)

全ての引き戻しの存在公理

(...)

全ての指数対象の存在公理

(...)

部分対象分類子の存在公理

(...)