雑記帳
圏論的にIf文を組み立てる

前置き
条件分岐を伴う対応の規則を矢印の合成規則として反映する射の存在を示すには...
以下のような「写像・関数 \(f\) の満たすべき関係」
\[
f(n) = 2n + 1
\]
が与えられたとし、もしその式に含まれる変数を上手く括りだすことが出来れば、その対応の規則を射の合成規則の結果として持つような具体的な射の形を見出すことができた。
\[
\begin{align}
f(n) &= 2n + 1 \\
n {\sf \, ⨟ \,} f &= \langle \langle 2,n \rangle {\sf \, ⨟ \,} (\cdot_{\mathbb{N}}), 1 \rangle {\sf \, ⨟ \,} (+_{\mathbb{N}}) \\
n {\sf \, ⨟ \,} f &= \langle n {\sf \, ⨟ \,} \langle {\rm const}(2),{\mathbb{N}} \rangle {\sf \, ⨟ \,} (\cdot_{\mathbb{N}}), 1 \rangle {\sf \, ⨟ \,} (+_{\mathbb{N}}) \\
n {\sf \, ⨟ \,} f &= n {\sf \, ⨟ \,} \langle \langle {\rm const}(2),{\mathbb{N}} \rangle {\sf \, ⨟ \,} (\cdot_{\mathbb{N}}), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+_{\mathbb{N}}) \\
n {\sf \, ⨟ \,} f &= n {\sf \, ⨟ \,} (\langle \langle {\rm const}(2),{\mathbb{N}} \rangle {\sf \, ⨟ \,} (\cdot_{\mathbb{N}}), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+_{\mathbb{N}})) \\
\end{align}
\]
一方、次のような条件分岐を含む関係式
\[
g(n) =
\begin{cases}
2n + 1 & \text{ if } n \le 5 \\
n & \text{ otherwise }
\end{cases}
\]
となった場合、今までと全く同じような方法を用いて与えられた条件を満足するような写像の存在を示すことは出来なくなる。
Excel の IF 関数のような写像が存在すると仮定すると上手くいく?
ではどうすればよいのかという話になるのだが、手っ取り早い1つの方法としては、「Excel の IF 関数」に相当する写像を使って分岐を表現するというものである。
例えば上の関数のとる値 \(g({\rm A1})\) は、Excel では
=IF(A1<=5,2*A1+1,A1)
という式で記述することができる。
同様に、もしその IF 関数に相当する写像 \({\rm if}:{\rm Bool}\times(A\times A)\rightarrow A\) の存在を仮定すると、圏論的にも
\[
g(n) = {\rm if}(n \le 5,\langle 2n+1, n \rangle)
\]
と書き表すことができるわけだが、この形であれば通常通り \(n\) を括りだすことができ、
\[
\begin{align}
g(n) &= {\rm if}(n \le 5,\langle 2n+1, n \rangle) \\
n {\sf \, ⨟ \,} g &= {\rm if}(\langle n,5 \rangle {\sf \, ⨟ \,} (\le),\langle \langle \langle 2,n \rangle {\sf \, ⨟ \,} (\cdot), 1 \rangle {\sf \, ⨟ \,} (+), n \rangle) \\
n {\sf \, ⨟ \,} g &= \langle \langle n,5 \rangle {\sf \, ⨟ \,} (\le),\langle \langle \langle 2,n \rangle {\sf \, ⨟ \,} (\cdot), 1 \rangle {\sf \, ⨟ \,} (+), n \rangle \rangle {\sf \, ⨟ \,} {\rm if} \\
n {\sf \, ⨟ \,} g &= \langle n {\sf \, ⨟ \,} \langle {\rm id}, {\rm const}(5) \rangle {\sf \, ⨟ \,} (\le),\langle n {\sf \, ⨟ \,} (\langle \langle {\rm const}(2),{\rm id} \rangle {\sf \, ⨟ \,} (\cdot), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+)), n \rangle \rangle {\sf \, ⨟ \,} {\rm if} \\
n {\sf \, ⨟ \,} g &= \langle n {\sf \, ⨟ \,} \langle {\rm id}, {\rm const}(5) \rangle {\sf \, ⨟ \,} (\le), n {\sf \, ⨟ \,} \langle \langle \langle {\rm const}(2),{\rm id} \rangle {\sf \, ⨟ \,} (\cdot), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+), {\rm id} \rangle \rangle {\sf \, ⨟ \,} {\rm if} \\
n {\sf \, ⨟ \,} g &= n {\sf \, ⨟ \,} \langle \langle {\rm id}, {\rm const}(5) \rangle {\sf \, ⨟ \,} (\le), \langle \langle \langle {\rm const}(2),{\rm id} \rangle {\sf \, ⨟ \,} (\cdot), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+), {\rm id} \rangle \rangle {\sf \, ⨟ \,} {\rm if} \\
\end{align}
\]
より
\[
g = \langle \langle {\rm id}, {\rm const}(5) \rangle {\sf \, ⨟ \,} (\le), \langle \langle \langle {\rm const}(2),{\rm id} \rangle {\sf \, ⨟ \,} (\cdot), {\rm const}(1) \rangle {\sf \, ⨟ \,} (+), {\rm id} \rangle \rangle {\sf \, ⨟ \,} {\rm if}
\]
というように射 \(g\) の存在が示せる。
そもそも if をどのように写像として構成するのか?
写像 \({\rm if}:{\rm Bool}\times(A\times A) \rightarrow A\) について、\(A\) が有限個の要素しか持たない場合であるとすると、技術的には
で説明した方法を使って構成することはできる。
具体例を1つ挙げると \(A\) が \((1+1)+1\) の場合は
\[
\begin{align}
A &:= (1+1)+1 \\
{\rm Bool} &:= 1+1 \\
\\
{\rm true} &:= {\rm inj}_1 \\
{\rm false} &:= {\rm inj}_2 \\
\\
0 &:= {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 \\
1 &:= {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 \\
2 &:= {\rm inj}_2 \\
\end{align}
\]
としたとき
\[
\begin{align}
{\rm if}({\rm true}, \langle 0,0 \rangle) &= 0 \\
{\rm if}({\rm false}, \langle 0,0 \rangle) &= 0 \\
{\rm if}({\rm true}, \langle 0,1 \rangle) &= 0 \\
{\rm if}({\rm false}, \langle 0,1 \rangle) &= 1 \\
{\rm if}({\rm true}, \langle 0,2 \rangle) &= 0 \\
{\rm if}({\rm false}, \langle 0,2 \rangle) &= 2 \\
{\rm if}({\rm true}, \langle 1,0 \rangle) &= 1 \\
{\rm if}({\rm false}, \langle 1,0 \rangle) &= 0 \\
{\rm if}({\rm true}, \langle 1,1 \rangle) &= 1 \\
{\rm if}({\rm false}, \langle 1,1 \rangle) &= 1 \\
{\rm if}({\rm true}, \langle 1,2 \rangle) &= 1 \\
{\rm if}({\rm false}, \langle 1,2 \rangle) &= 2 \\
{\rm if}({\rm true}, \langle 2,0 \rangle) &= 2 \\
{\rm if}({\rm false}, \langle 2,0 \rangle) &= 0 \\
{\rm if}({\rm true}, \langle 2,1 \rangle) &= 2 \\
{\rm if}({\rm false}, \langle 2,1 \rangle) &= 1 \\
{\rm if}({\rm true}, \langle 2,2 \rangle) &= 2 \\
{\rm if}({\rm false}, \langle 2,2 \rangle) &= 2 \\
\end{align}
\]
を満たす射として \({\rm if}\) が構成される。
一方で、\(A\) が非有限個の要素を持つ場合、上記の「愚直に対応を全て列挙する方法」は通用しなくなる。
つまり、冒頭に挙げた
\[
g(n) =
\begin{cases}
2n + 1 & \text{ if } n \le 5 \\
n & \text{ otherwise }
\end{cases}
\]
を満たす写像 \(g\) の構成に必要になる \({\rm if}\) の存在は依然として示せない。
因みに、「非有限の場合でも、単に写像のグラフを構成してしまえば良いのでは?」と思う人がいるかもしれないが、その方法では「逆射」の存在の証明が付きまとうし、そもそも「部分対象の操作 (共通部分や合併の誘導など)」を柔軟に行うためには周囲圏に対して「トポス」というあまりにも強すぎる設定が必要になる。
できれば「トポス」という強い設定ではなく、関数型プログラミング言語にも適用可能なより課される条件の少ない (Haskell で機械的に検証可能な) 設定で、さらに欲を言えば「直接的な構成」のできる方が好ましい。
幸運にも、そういった条件分岐を含む関係式によって特徴付けられる関数の圏論的な組み立てに必要になる写像 \({\rm if}\) は、「全ての有限余積と自然数対象を持つカルテシアン閉圏」という設定の下でかなり簡単に構成することができる。
この記事では、その幾つかについてを簡単に紹介していきたい。
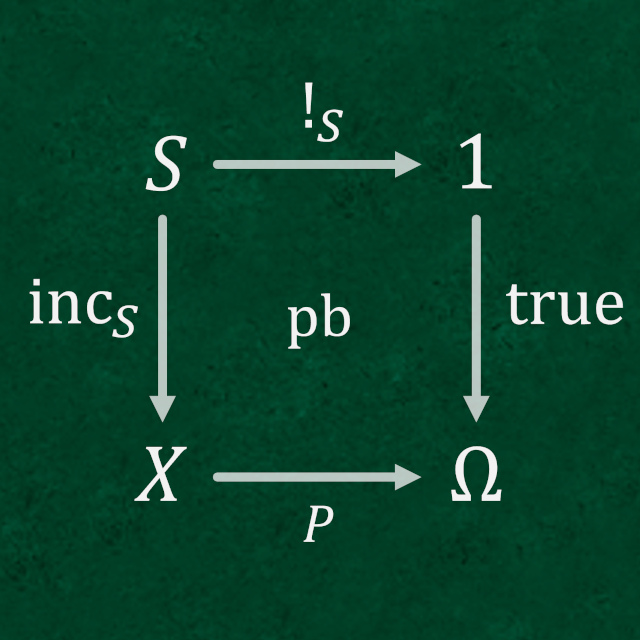
真偽値を余積対象 1+1 の要素として受け取る If-Else 条件分岐
これは普通に「射影 \(A\times A\rightarrow A\)」を要素に変換して得られる2つの指数対象の要素から引き起こされる「余積対象 \(1+1\) からの射 \(1+1\rightarrow A^{A\times A}\)」に対して un-カリー化をとって得られる
\[
{\rm if}_2 = \left(\left(\begin{matrix} {\rm arrToEl}({\rm prj}_1) \cr {\rm arrToEl}({\rm prj}_2) \end{matrix}\right) \times (A \times A)\right) {\sf \, ⨟ \,} {\rm ev}
\]
として構成できる。
但し、ここで使っている \({\rm arrToEl}(f)\) の定義については、
を参照。
余談
当たり前だが、\(A\times A \rightarrow A\) ではなく \(A\times B \rightarrow A\), \(A\times B \rightarrow B\) という型の射影を用いて分岐を作ることは、型に不整合が生じてしまうことからわかるように不可能となる。
これについては、Haskell のような強い型付けがされるプログラミング言語における If-Else 分岐に慣れている人にとってはしっくりくることと思う。
とはいえこのままでは使い勝手が良くないので、応用のためには次節で説明するちょっとした小細工が必要になる。
真偽値をC言語ライクに自然数として受け取る If-Else 条件分岐
導入
先ほど紹介した「真偽値を終対象同士の余積対象の要素として受け取る条件分岐」には、応用が利きづらいという難点がある。
というのも、現在の「全ての有限余積と自然数対象を持つカルテシアン閉圏」という設定では、そもそもトポスが持つような論理演算子が定義されない。
即ち条件分岐が作れたとしても、「\(1+1\) をコドメインにとる射」という形の条件式がそもそもとして柔軟に組めないので、応用のしようがないという状況になってしまっている。
幸運なことに現在の設定の下でも、C言語ライクに
- 自然数 0 を偽
- それ以外の自然数を真
と見做すことで、
- 論理積
- 論理和
- 否定
- 相等関係
- 順序関係
といった条件式を組み立てる上で重要な役割を果たすパーツを組み立てることはできる。(これら射の具体的な構成方法は「自然数対象を持つカルテシアン閉圏の一般論の中でアッカーマン関数を構成する。」を参照。)
そのため、「真偽値をC言語ライクに自然数として受け取る If-Else 条件分岐」であれば、かなり柔軟に射の構成へと応用できることが期待される。
構成
具体的な構成は以下のようになる。
基本的には先ほどの構成と変わらないが、一つ異なるのは、「自然数として表された真偽を余積対象の要素として表された真偽に変換する射 \({\mathbb{N}}\rightarrow 1+1\)」を途中でかませるという点である。
そのデータ変換用の射は
\[
{\rm rec}_{{\mathbb{N}}}({\rm inj}_2,\nabla {\sf \, ⨟ \,} {\rm inj}_1)
\]
として構成でき、よって条件分岐 \({\rm if}_{{\mathbb{N}}}:{\mathbb{N}}\times(A\times A) \rightarrow A\) は
\[
{\rm if}_{{\mathbb{N}}} = \left(\left({\rm rec}_{{\mathbb{N}}}({\rm inj}_2,\nabla {\sf \, ⨟ \,} {\rm inj}_1) {\sf \, ⨟ \,} \left(\begin{matrix} {\rm arrToEl}({\rm prj}_1) \cr {\rm arrToEl}({\rm prj}_2) \end{matrix}\right)\right) \times (A \times A)\right) {\sf \, ⨟ \,} {\rm ev}
\]
となる。
余談
アッカーマン関数を構成する記事では、周囲圏に対して「全ての有限余積の存在」を仮定していないため、少しぎこちないスタイルで If-Else を無理やりに表現しているが、余積の存在を仮定すればこのような「出力される値の型に対して "自然数でなければいけない" という縛りのない If」を用いて記述することが可能になる。
応用
自然数対象を添字集合とする対象の要素の族
この If-Else 条件分岐は自然数対象を添字集合とする対象 \(X\) の要素の族 \({\mathbb{N}}\rightarrow X\) を組み立てる際に便利となる。
例えば
\[
a_n =
\begin{cases}
\langle 2,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1 & \text{ if } n=0 \\
\langle 9,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1 & \text{ if } n=1 \\
16 {\sf \, ⨟ \,} {\rm inj}_2 & \text{ if } n=2 \\
\langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 & \text{ otherwise }
\end{cases}
\]
という条件を満たす族 \(a:{\mathbb{N}}\rightarrow (({\mathbb{N}}\times{\mathbb{N}})+{\mathbb{N}})\) は
\[
a(n) = {\rm if}_{{\mathbb{N}}}(n==0,\langle \langle 2,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1, {\rm if}_{{\mathbb{N}}}(n==1,\langle \langle 9,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1,{\rm if}_{{\mathbb{N}}}(n==2,\langle 16 {\sf \, ⨟ \,} {\rm inj}_2, \langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \rangle) \rangle) \rangle)
\]
と書き変わるが、この式であれば \(a\) の形を通常通り求められる。
\[
\begin{align}
a(n) &= {\rm if}_{{\mathbb{N}}}(n==0,\langle \langle 2,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1, {\rm if}_{{\mathbb{N}}}(n==1,\langle \langle 9,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1,{\rm if}_{{\mathbb{N}}}(n==2,\langle 16 {\sf \, ⨟ \,} {\rm inj}_2, \langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \rangle) \rangle) \rangle) \\
n {\sf \, ⨟ \,} a &= n{\sf \, ⨟ \,} (\langle \langle {\mathbb{N}},{\rm const}(0)\rangle {\sf \, ⨟ \,} (=='), \langle {\rm const}(\langle 2,2\rangle {\sf \, ⨟ \,} {\rm inj}_1),\langle \langle {\mathbb{N}},{\rm const}(1)\rangle {\sf \, ⨟ \,} (=='), \langle {\rm const}(\langle 9,2\rangle {\sf \, ⨟ \,} {\rm inj}_1),\langle \langle {\mathbb{N}},{\rm const}(2)\rangle {\sf \, ⨟ \,} (=='), {\rm const}(\langle 16{\sf \, ⨟ \,} {\rm inj}_2, \langle 0,0\rangle {\sf \, ⨟ \,} {\rm inj}_1\rangle )\rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}} \rangle \rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}} \rangle \rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}})
\end{align}
\]
つまり
\[
a = \langle \langle {\mathbb{N}},{\rm const}(0)\rangle {\sf \, ⨟ \,} (=='), \langle {\rm const}(\langle 2,2\rangle {\sf \, ⨟ \,} {\rm inj}_1),\langle \langle {\mathbb{N}},{\rm const}(1)\rangle {\sf \, ⨟ \,} (=='), \langle {\rm const}(\langle 9,2\rangle {\sf \, ⨟ \,} {\rm inj}_1),\langle \langle {\mathbb{N}},{\rm const}(2)\rangle {\sf \, ⨟ \,} (=='), {\rm const}(\langle 16{\sf \, ⨟ \,} {\rm inj}_2, \langle 0,0\rangle {\sf \, ⨟ \,} {\rm inj}_1\rangle )\rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}} \rangle \rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}} \rangle \rangle {\sf \, ⨟ \,} {\rm if}_{{\mathbb{N}}}
\]
として構成される。
Haskell での動作確認
Haskell の型とその間の関数は (理想的には) 「全ての有限余積と自然数対象を持つカルテシアン閉圏」をなすため、以上の構成は Haskell でもそのまま適用可能である。
ということで、「自然数対象を添字集合とする対象の要素の族」の例として構成した射を実際に Haskell の関数として組み立てて、ちゃんと動作するのかを検証しておく。
以下はこのページの終わりに載せたコードを、GHC のインタラクティブモードから読み込んで実行した結果である。
ghci> printEl $ nat(0) -: a'
(2,2);inj1
ghci> printEl $ nat(1) -: a'
(9,2);inj1
ghci> printEl $ nat(2) -: a'
16;inj2
ghci> printEl $ nat(3) -: a'
(0,0);inj1
ghci> printEl $ nat(4) -: a'
(0,0);inj1
ghci> printEl $ nat(5) -: a'
(0,0);inj1この結果からわかるように、
\[
\begin{align}
a(0) &= \langle 2,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \\
a(1) &= \langle 9,2 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \\
a(2) &= 16 {\sf \, ⨟ \,} {\rm inj}_2 \\
a(3) &= \langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \\
a(4) &= \langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \\
a(5) &= \langle 0,0 \rangle {\sf \, ⨟ \,} {\rm inj}_1 \\
\end{align}
\]
という最初に与えた関係式が満たされている事の確認が取れる。
ソースコード
{-# LANGUAGE TypeOperators #-}
import Data.Void
main :: IO ()
main = do
printEl $ nat(0) -: a'
printEl $ nat(1) -: a'
printEl $ nat(2) -: a'
printEl $ nat(3) -: a'
printEl $ nat(4) -: a'
printEl $ nat(5) -: a'
class (MyShow a) where
myShow :: a -> String
instance MyShow () where
myShow = const "*"
instance (MyShow a, MyShow b) => MyShow (Either a b) where
myShow = either
(\z -> if (myShow z == "*") then "inj1" else (myShow z) ++ ";inj1")
(\z -> if (myShow z == "*") then "inj2" else (myShow z) ++ ";inj2")
instance (MyShow a, MyShow b) => MyShow (a,b) where
myShow (x,y) = "(" ++ myShow x ++ "," ++ myShow y ++ ")"
instance MyShow Int where
myShow = show
instance MyShow Nat where
myShow (Nat i) = myShow (length i)
--myShow (Nat i) = "zero" ++ (foldr ((++).(const ";succ")) [] i)
instance MyShow (a -> b) where
myShow = const "(AN ARROW)"
-- X の要素を圏論に倣って終対象から X への射(Global element)として扱うための関数
el :: a -> (Pt -> a)
el = (const::a -> (Pt -> a))
-- Global elements 用 ユーティリティ
(===) :: Eq a => (Pt -> a) -> (Pt -> a) -> Bool
(===) x y = (x() == y())
showEl :: MyShow a => (Pt -> a) -> String
showEl x = (myShow $ x())
printEl :: MyShow a => (Pt -> a) -> IO ()
printEl = putStrLn . showEl
-- Diagrammatic-order な射の合成演算
(-:) = flip (.)
-- # 始対象と終対象
type Empty = Void
type Pt = ()
initArr :: Empty -> a
initArr = absurd
termArr :: a -> Pt
termArr = const ()
point :: Pt -> Pt
point = id
const' x = termArr -: x
-- # 余積対象と積対象
type (+++) a b = Either a b
type (***) a b = (a,b)
-- 入射
inj1 :: a -> a +++ b
inj1 = Left
inj2 :: b -> a +++ b
inj2 = Right
-- 射影
prj1 :: a *** b -> a
prj1 = fst
prj2 :: a *** b -> b
prj2 = snd
-- 余積対象の仲介射
coPair :: (a -> c, b -> c) -> (a +++ b -> c)
coPair = uncurry either
-- 積対象の仲介射
pair :: (c -> a, c -> b) -> (c -> a *** b)
pair = uncurry $ (<*>) . fmap (,)
-- 畳み込み
fol = coPair(id, id)
-- 対角射
dup = pair(id, id)
-- 射同士の余積
(+++) :: (a1 -> b1) -> (a2 -> b2) -> (a1 +++ a2 -> b1 +++ b2)
(+++) f g = coPair(f -: inj1 , g -: inj2)
-- 射同士の積
(***) :: (a1 -> b1) -> (a2 -> b2) -> (a1 *** a2 -> b1 *** b2)
(***) f g = pair(prj1 -: f, prj2 -: g)
-- Twist の形式的双対
coTw :: a +++ b -> b +++ a
coTw = coPair(inj2, inj1)
-- Twist
tw :: a *** b -> b *** a
tw = pair(prj2, prj1)
-- # Exponential 対象
type (^) b a = a -> b
-- 評価射
ev :: (b ^ a) *** a -> b
ev = uncurry id
-- 射の転置 (transpose) の構成
trans :: (c *** a -> b) -> (c -> b ^ a)
trans = curry
-- 射 h:a->b の Exponential 対象 (Exp b a) の要素への変換
arrToEl :: (a -> b) -> (Pt -> b ^ a)
arrToEl h = trans(prj2-:h)
elToArr x = pair(termArr, id) -: (x *** id) -: ev
-- # 自然数対象 (NNO)
data Nat = Nat{imp::[()]} deriving Eq
_Nat :: Nat -> Nat
_Nat = id
zero :: Pt -> Nat
zero = el (Nat [])
succ' :: Nat -> Nat
succ' (Nat i) = Nat (():i)
-- 整数リテラルを使って NNO の Global elements としての自然数を得るための小細工
nat :: Int -> (Pt -> Nat)
-- nat i = zero -: (foldr (.) id (replicate i succ'))
nat i = el (Nat (replicate i ()))
-- recursion data x_0:1->X と f:X->X から rec_N(x_0, f):Nat->X を構成する関数
rec_N :: (Pt -> a, a -> a) -> (Nat -> a)
rec_N = ((flip ($) ())***id)-:((curry((id***(length.imp))-:uncurry(!!))).(uncurry.flip $ iterate))
add_N = (rec_N(arrToEl(_Nat), trans(ev-:succ'))***_Nat)-:ev
mul_N = (rec_N(arrToEl(termArr-:nat(0)), trans(pair(ev,prj2)-:add_N))***_Nat)-:ev
mul_N_fast (Nat x, Nat y) = Nat (replicate (length x * length y) ()) -- デバッグ用
sq_N = dup-:mul_N
pred' = rec_N(pair(nat(0),nat(0)), pair(prj2, prj2 -:succ')) -: prj1
sub_N = tw-:(rec_N(arrToEl(_Nat), trans(ev-:pred'))***_Nat)-:ev
true :: Pt -> Nat
true = nat(1)
false :: Pt -> Nat
false = nat(0)
le' :: Nat *** Nat -> Nat
le' = sub_N -: not'
eq' :: Nat *** Nat -> Nat
eq' = pair(le',tw-:le')-:and'
not' :: Nat -> Nat
not' = rec_N(pair(nat(1),nat(0)), pair(prj2, prj2)) -: prj1
and' :: Nat *** Nat -> Nat
and' = mul_N
or' :: Nat *** Nat -> Nat
or' = add_N
if_N :: (Nat *** (a *** a)) -> a
if_N = ((rec_N(inj2,fol-:inj1) -: coPair(arrToEl(prj1),arrToEl(prj2)))***id)-:ev
a' =
pair(pair(id,const'(nat(0)))-:eq',pair(const'(pair(nat(2),nat(2))-:inj1),pair(pair(id,const'(nat(1)))-:
eq', pair(const'(pair(nat(9),nat(2))-:inj1),pair(pair(id,const'(nat(2)))-:
eq', const'(pair(nat(16)-:inj2, pair(nat(0),nat(0))-:inj1)))-:if_N))-:if_N))-:if_Nタグ一覧: