雑記帳
圏論的和と圏論的積 (余積と積)

目次
•
•
•
•
•
•
•
•
(書きかけ)
前置き
このページでは、\(A,B\) を圏の対象としたとき
- 2つのそれぞれの対象の一般化要素を要素に持つ対象 (余積対象)
- 2つの対象からぞれぞれ選び出された一般化要素の順序対を要素に持つ対象 (積対象)
といった「具体的に意味が指定された対象」が圏論的にどのようにして導入されるのかを考えていく。
この部分は慣れないと少しわかりにくい側面もあり、話は慎重に進めていく方針をとる。
圏の対象は内部構造をもたない?
まず思い出してほしいのだが、「圏の対象」というのは結局のところは「単なる点」でしかない。
これの何が問題なのかというと、よく素朴集合論で披露されるような
\[
X := \{ (a,b) \:|\: a\in A, b\in B \}
\]
といった「内部構造 (internal structure)」を与えた対象の構成は、圏の一般論の中では通常できないということである。
というのも、圏の中の住人、即ち圏の中に存在できるモノは「適切な条件を満たす矢印」だけに限られ、そもそもとして圏という構造の中に「内部構造の置き場となる場所」がない。
どういうことかをもう少し噛み砕くと、通常僕たちが「対象の内部構造」と呼ぶモノは、圏の理論とはまた別の「物質的集合論」の枠組みの中で使用が認められる「具体集合」を指す場合が多い。
ここで具体集合は「ZFC のような基礎が敷かれた上で初めて存在できる住人」であり、すべての圏に標準でインストールされているものではない。(単なる「圏の公理」が ZFC の公理を導かないという点からも察しがつくはずである。)
仮にもし「すべての圏には、あらゆる具体集合が圏のパーツとして組み込まれている」ということが事実であるとするならば、その全ての具体集合が「ドメイン・コドメイン・合成が適切に定義されている矢印」として存在していなければならないのだが、例えば以下に示す区間圏を眺めてみてほしい。
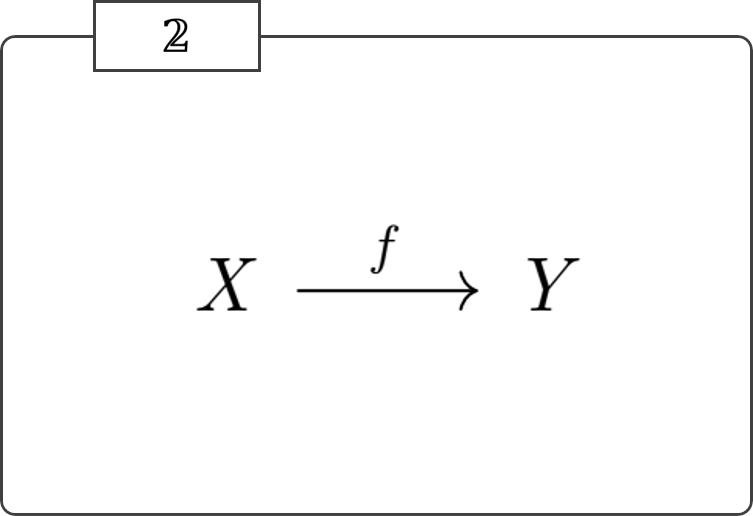
その圏の中に、空集合や自然数全体の集合などの具体集合に相当するパーツが含まれているだろうか?
見ての通り、その住人は
- \(X:X\rightarrow X\)
- \(Y:Y\rightarrow Y\)
- \(f:X\rightarrow Y\)
の3人だけであり、それ以外に住んでいる人は誰一人としていない。
もう一つ例を挙げておくと、例えば以下の圏の中の対象 \(X_5\) というものは、何か内部構造なるものを持っているだろうか?
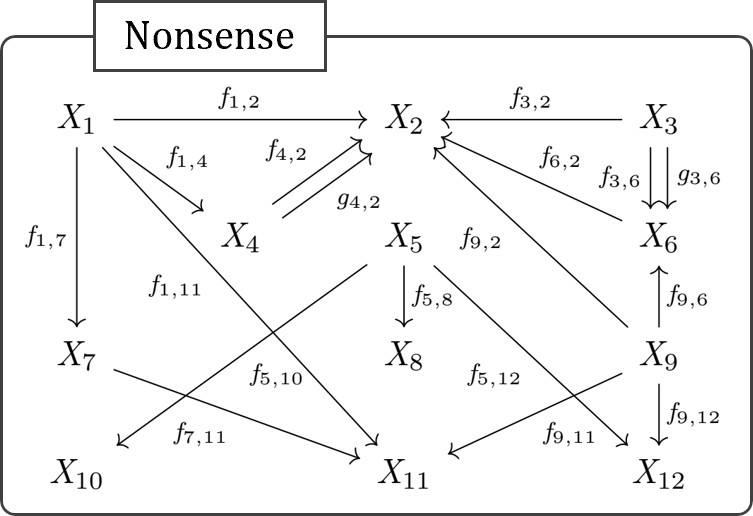
もちろんそんなものは無く、圏の形が複雑になろうが、圏の持つ対象が単なる有向グラフ内の一点でしかないことには変わりない。
要約すれば、先行する「具体集合の概念」が、圏という構造の内部には存在しないので、圏の一般論において、「対象に意味を与える手掛かり」として使用できるモノは、(エピックやモニックの概念を定式化した時と同様) 「矢印 (圏の住人) と、合成演算を始めとする圏の持つ演算構造」の他、何一つとして存在しないということである。
ここで、
- エピックやモニックのような単純なものならともかく、複雑な数学概念の定式化を (集合の使用なしに) それら「圏の持つ構造」だけで完結させるなど無理でしょ
と考える人もいると思うが、驚くことに現状知られている殆ど全ての数学概念は、この「矢印の合成」を使った条件式で記述できてしまうことがわかっている。
そしてこの事実こそが、圏論を強力なものにしている理由の一つでもあるだろう。
続いて、どのようにして「具体的に意味が指定された対象」を純粋圏論的に定式化し取り扱っていくのかという話だが、この部分については本題となる「余積対象」や「積対象」を説明していく中で確認していく。
余積 (coproduct)
導入
\(A,B\) を圏の対象としたとき、それらの 圏論的和 (category-theoretic sum / categorical sum) あるいは 余積 (coproduct) とは、意味合いとしては
- 「対象 \(A,B\) のそれぞれの一般化要素を全て要素として持っている」というような意味付けがされた対象
である。
前置きでも述べた通り、純粋圏論的には対象に対して内部構造を組み込むことはできず、
- 圏の持つ矢印
- 圏の持つ矢印の始点と終点を求める演算
- 圏の持つ矢印の合成演算
という圏の構成要素だけを用いることによって、この状況を上手く定式化していかなければならない。
では具体的にどのようにして形にしていくのかを、順を追って考えていく。
まず「ある対象 \(X\) が、対象 \(A,B\) のそれぞれの一般化要素を全て要素として持つ」という状況を作るためには、以下の図式
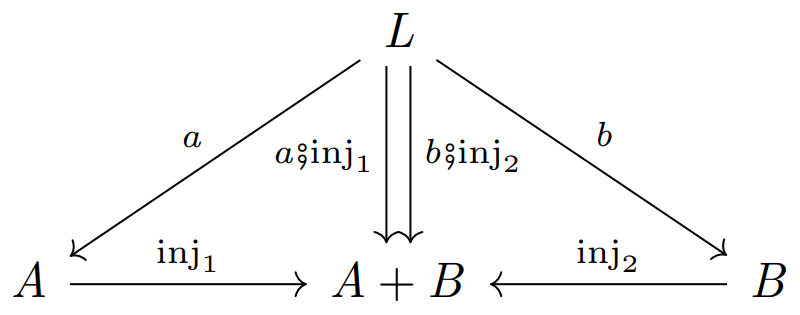
を見ての通り
- \(A\) から伸びる矢印 \(u_1:A\rightarrow X\)
- \(B\) から伸びる矢印 \(u_2:B\rightarrow X\)
の2つの矢印が点 \(X\) の周りに最低限存在していることが要求される。
もちろん、漠然と「2つの矢印 \(u_1,u_2\) が存在している」と宣言しただけでは意味付けとしては全く不十分である。
具体的にどのように不十分であるのかについては、例えば
- \(a{\sf \, ⨟ \,} u_1\) が \(a\) と同様の振舞いをする確証がない。
- 図式内の2つの \(A+B\) の一般化要素が等しいのか否かの明確な判定基準がない。
- \(A+B\) の一般化要素 \(x:L\rightarrow A+B\) が射 \(f:A+B\rightarrow C\) との合成に対してどのように振舞うのかが未定義である。(\(A+B\) から伸びる射の一般的な組み立て方法が確立していない。)
などが挙げられる。
つまり、その2つの矢印 \(u_1,u_2\) に対する、明確な「意味付け」が必要ということである。
具体的な意味付け方法については、次のように考えることができる。
「対象 \(A,B\) のそれぞれの一般化要素を全て要素として持っている対象」を謳っているわけだから、\(u_1,u_2\) を通して得られる \(X\) の一般化要素の振舞いというのは、対応する \(A\) あるいは \(B\) の一般化要素のそれでなければおかしい。
逆に考えれば、\(\Lambda\) を任意の対象とし、
- \(A\) 側の一般化要素を \(\Lambda\) の一般化要素に変換する矢印 \(\alpha: A\rightarrow \Lambda\)
- \(B\) 側の一般化要素を \(\Lambda\) の一般化要素に変換する矢印 \(\beta: B\rightarrow \Lambda\)
の2つの矢印が与えられれば、任意の \(a:L\rightarrow A\), \(b:L\rightarrow B\) について
\[
\begin{align}
(a {\sf \, ⨟ \,} u_1) {\sf \, ⨟ \,} h = a {\sf \, ⨟ \,} \alpha \\
(b {\sf \, ⨟ \,} u_2) {\sf \, ⨟ \,} h = b {\sf \, ⨟ \,} \beta \\
\end{align}
\]
という関係式を満足する (\(X\) の一般化要素を \(\Lambda\) の一般化要素へと変換する) 矢印 \(h:X\rightarrow \Lambda\) が一意的に定まるべきということである。
ここで、上の関係式を「圏の射の結合性公理」という点に注目した上で、変形すると
\[
\begin{align}
a {\sf \, ⨟ \,} (u_1 {\sf \, ⨟ \,} h) = a {\sf \, ⨟ \,} \alpha \\
b {\sf \, ⨟ \,} (u_2 {\sf \, ⨟ \,} h) = b {\sf \, ⨟ \,} \beta \\
\end{align}
\]
となるわけだが、もし以下の
\[
\begin{align}
u_1 {\sf \, ⨟ \,} h = \alpha \\
u_2 {\sf \, ⨟ \,} h = \beta \\
\end{align}
\]
という関係式が満たされていれば、先ほど示した関係式が、任意の \(a,b\) に対して恒等的に成り立つことはわかるだろう。
この場面において、\(u_1,u_2\) という2つの矢印は、振舞いが全くの "未定義" の矢印であり、振舞いを指示するだけの余白は残っているわけだから、この関係式を「\(u_1,u_2\) の満たすべき性質」としてそのまま課してしまえばそれで事が済む、
纏めると、
圏の中の任意の矢印 \(\alpha:A\rightarrow \Lambda\), \(\beta:B\rightarrow \Lambda\) に対して、
\[
\begin{align}
\alpha &= u_1 {\sf \, ⨟ \,} h \\
\beta &= u_2 {\sf \, ⨟ \,} h \\
\end{align}
\]
という関係式を満たす矢印 \(h:X\rightarrow \Lambda\) が一意的に存在する。
という条件を \(u_1,u_2\) に課すことで、それらが「対象 \(A,B\) のそれぞれの一般化要素を、求める形で \(X\) の一般化要素へと変換する矢印」としての意味を持つことができる。
定義
ある圏において、2つの対象 \(A,B\) が与えられたとき、\(A\) と \(B\) の余積とは、任意の射 \(\alpha:A\rightarrow \Lambda\), \(\beta:B\rightarrow \Lambda\) について、以下の図式
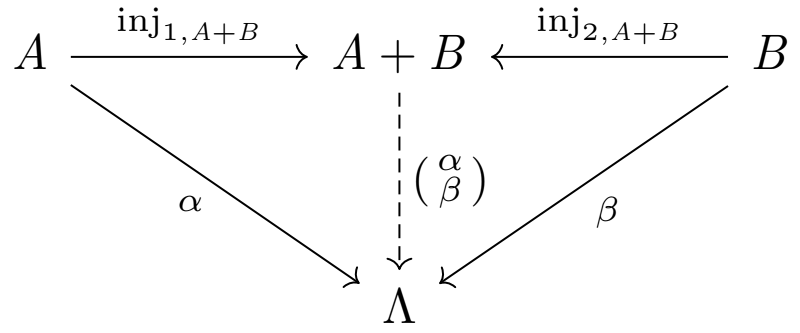
を可換にする一意的な射 \(A+B\rightarrow \Lambda\) の存在を保証するような
- 対象 \(A+B\)
- 射 \({\rm inj}_{1,A+B}:A\rightarrow A+B\)
- 射 \({\rm inj}_{2,A+B}:B\rightarrow A+B\)
という3つの射一式からなる構造であり、\(A+B\) は余積対象、\({\rm inj}_{1,A+B}\) と \({\rm inj}_{2,A+B}\) は 入射 (injection) や余射影 (coprojection) などと呼ばれる。
\(\alpha,\beta\) に対して一意的に定まる射は、\(\alpha,\beta\) によって引き起こされる射と呼ばれ、\(\left(\begin{matrix} \alpha \cr \beta \end{matrix}\right)\) や \([\alpha,\beta]\) などと書かれる。
入射について、わざわざ型を明示しなくても Haskell の型推論と同様、正確に推論できてしまうことが殆どであるため、式を見やすくするためにも基本的にここでは \({\rm inj}_1, {\rm inj}_2\) というように型を省略した記号を使用する。
図式を使わずに、数式を直接用いてそのまま書くとするならば
\[
\begin{align}
\alpha &= {\rm inj}_1 {\sf \, ⨟ \,} h \\
\beta &= {\rm inj}_2 {\sf \, ⨟ \,} h \\
\end{align}
\]
という関係式を満たす矢印 \(h:A+B\rightarrow \Lambda\) が一意的に存在するという意味で、この条件はしばしば「余積の普遍性」と呼ばれる。
注意点としては、余積対象 \(A+B\) は「余積の普遍性を満たす射一式の1つ」であり、わかりやすく言い換えると
- \(A+B\) という対象を持ち出した場合、同時に指定の普遍性を満足する二つの矢印 \({\rm inj}_1, {\rm inj}_2\) の存在も保証される
ということである。
なぜこんなことを強調しているのかといえば、圏論初学者がしばしば
- 入射 \({\rm inj}_1, {\rm inj}_2\) は、何処からやってきたんだ? それら写像の定義ぐらいは最低限しっかりとしようよ。
と誤解しがちであるためである。
実際のところは、
- 余積の普遍性を満たす矢印である2つの入射 \({\rm inj}_1, {\rm inj}_2\) の存在を仮定することが許されている対象を \(A+B\) として定義している
ということなので、「何処からやってきたのか」ということを考えるまでもなく、定義から \(A+B\) という対象の周りには必ずその普遍性を満たす矢印が存在している。
(..)
余談
余積のことを直和と呼ぶこともあるが、その一方で、それら2つを明確に異なる数学概念として区別した形で定義する流儀も存在する。
ここでは区別する流儀の方を採用しているため、余積を直和と呼ぶことは控えることにしている。
(..)
一階の言語による記述
入射であるために課される条件を2つの射が満たしているのかを判定する式
\[
{\rm areInj}(i,j,X,A,B) :\Leftrightarrow \forall A \forall B[\forall f \forall g \forall \Lambda [(f:A\rightarrow \Lambda \wedge g:B\rightarrow \Lambda) \Rightarrow\exists ! h [h:X\rightarrow \Lambda \wedge {\rm \_comp}(i,h,f) \wedge {\rm \_comp}(j,h,g)]]]
\]
与えられた対象が余積対象であるのかを判定する式
\[
{\rm isSumObj}(X,A,B) :\Leftrightarrow \exists i \exists j[{\rm areInj}(i,j,X,A,B)]
\]
引き起こされた射であるのかを判定する式
\[
{\rm isCoparing}(h,f,g,i,j,X,A,B) :\Leftrightarrow {\rm areInj}(p,q,X,A,B) \wedge {\rm \_comp}(i,h,f) \wedge {\rm \_comp}(j,h,g)
\]
和に関する重要な射の構成
射の和
\(f:A_1\rightarrow B_1\), \(g:A_2\rightarrow B_2\) を任意の射としたとき、次で定義される射 \((f+g):A_1+A_2 \rightarrow B_1+B_2\) は \(f\) と \(g\) の和と呼ぶ。
\[
f+g :=
\left(
\begin{matrix}
f {\sf \, ⨟ \,} {\rm inj}_1 \cr
g {\sf \, ⨟ \,} {\rm inj}_2
\end{matrix}
\right)
\]
余対角射 (co-diagonal arrow)
次で定義される射 \(\nabla:A+A\rightarrow A\) は 余対角射 (codiagonal arrow) または畳み込み (fold arrow) と呼ばれる。
\[
\nabla :=
\left(
\begin{matrix}
A \cr
A
\end{matrix}
\right)
\]
この射について、恐らく「これが一体、どんな場面で役に立つのか」と疑問に思う人は少なくないだろう。
実際、後に登場する、「圏論的積に関する仲介射」はかなり実用に富んだ射である一方で、それと比較した場合そもそも「圏論的和に関する仲介射」が使用される場面は恐らくそこまで多くない。
とはいえ、一見すると余積の必要性を表面上感じないような思いもよらない場面で、余積が必要になる場合がある。
具体例を1つ挙げると、以下の記事で説明しているように「従来の数学では、当たり前にできることとして注意深く考えていなかった If-Else 条件分岐」を厳密に噛み砕く場面において、余積の考えが顔を出す。
特に「自然数で添え字付けられた、ある集合の要素の族の内、条件分岐を伴うもの」を構成する際に使用している写像 \(\text{if}:{\mathbb{N}}\times(A\times A)\rightarrow A\) に注目してみてほしい。
その写像は、そのドメインとコドメインのそれぞれに余積の構成が含まれていないため、表面上は「余積」の出番などないように思えるが、実は構成を確認してみると気付くように、余対角射の応用例の1つになっている。
他にも、自明なことではあるがこの余対角射は、余積に関する仲介射を
\[
\left(
\begin{matrix}
\alpha \cr
\beta
\end{matrix}
\right) = (\alpha + \beta) {\sf \, ⨟ \,} \nabla
\]
というように分解するのに用いることもできる。
余談
\(A+B\) を余積対象としたとき、入射は一般にモニックとは云えないため、\((A,{\rm inj}_1)\) や \((B,{\rm inj}_2)\) は\(A+B\) の部分対象にはならない。とはいえ、分配的圏 (distributive category) と呼ばれる特別な性質を満たすような圏に対しては一般にそれが正しいことを証明することができる。
面白い例を先に一つ紹介すると、通常集合 \(A\) は非交和 \(A+A\) の物質的集合論の意味での部分集合にはならない話は有名であるが、例えば集合の圏は分配的圏であるため、\((A,{\rm inj}_1)\) はしっかりと余積対象 \(A+A\) の部分対象になる。
つまり \((A,{\rm inj}_1) \subseteq (A+A,{\rm id})\) が満たされる。
つまり \((A,{\rm inj}_1) \subseteq (A+A,{\rm id})\) が満たされる。
積 (product)
導入
\(A,B\) を圏の対象としたとき、それらの 圏論的積 (category-theoretic product / categorical product) あるいは単に 積 (product) とは、意味合いとしては
- 「対象 \(A,B\) からぞれぞれ一つずつ選び出された一般化要素の順序対を全て要素として持っている」というような意味付けがされた対象
である。
余積の節の繰り返しになるが、純粋圏論的には対象に対して内部構造を組み込むことはできないので、
- 圏の持つ矢印
- 圏の持つ矢印の始点と終点を求める演算
- 圏の持つ矢印の合成演算
という圏の構成要素だけを用いて、この状況を上手く定式化していくことになる。
では具体的にどのようにして形にしていくのかを、余積同様に順を追って考えていく。
まず「ある対象 \(X\) が、対象 \(A,B\) からぞれぞれ一つずつ選び出された一般化要素の順序対を全て要素として持つ」という状況を作るために何が必要であるのか。
余積の場合は、
- 余積対象の一般化要素は、先行して与えられている \(A,B\) のそれぞれの一般化要素から直接誘導される
であった一方、積の場合は、
- 積対象の一般化要素は、順序対、つまり一つの一般化要素が \(A,B\) のそれぞれの一般化要素へと分解される
ということになる。
この状況を実現するためには以下の図式
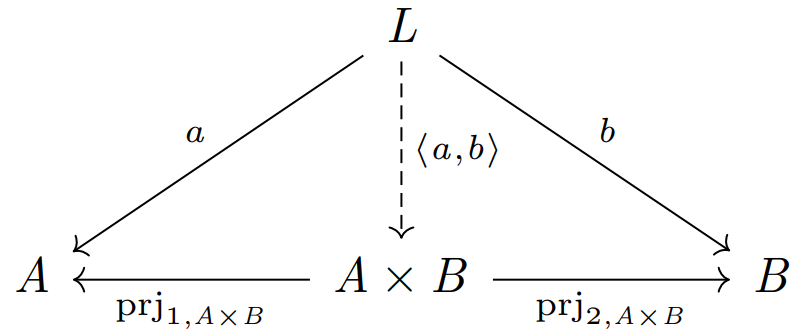
を参考にすればわかるが、まず
- \(A\) へと伸びる矢印 \(u_1:X\rightarrow A\)
- \(B\) へと伸びる矢印 \(u_2:X\rightarrow B\)
の2つの矢印が点 \(X\) の周りに最低限存在していることが要求される。
その上で、\(X\) の一般化要素 \(x:L\rightarrow X\) が
\[
\begin{align}
x {\sf \, ⨟ \,} u_1 = a \\
x {\sf \, ⨟ \,} u_2 = b \\
\end{align}
\]
という条件を満たす \(a,b\) に対して一意的に定まる矢印であるとすればそれで完了である。
補足するまでもないかもしれないが、「勝手にそんな条件を課して大丈夫なのか」という心配は余積の節で行った説明と同様の理由から問題ない。
つまり、そもそも \(u_1,u_2\) という2つの矢印は、振舞いが "未定義" であり、好きなように振舞いを指示する余白は残っている。
ここまでを纏めると、
圏の中の任意の矢印 \(a:L\rightarrow A\), \(b:L\rightarrow B\) に対して、
\[
\begin{align}
a &= u_1 {\sf \, ⨟ \,} x \\
b &= u_2 {\sf \, ⨟ \,} x \\
\end{align}
\]
という関係式を満たす矢印 \(x:L\rightarrow X\) が一意的に存在する。
という条件を \(u_1,u_2\) に課すことで、「\(Z\) の要素を、対象 \(A,B\) の一般化要素の対と見做せる」という状況を作ることができる。
定義
ある圏において、2つの対象 \(A,B\) が与えられたとき、\(A\) と \(B\) の積とは、任意の射 \(a:L\rightarrow A\), \(b:L\rightarrow B\) について、以下の図式
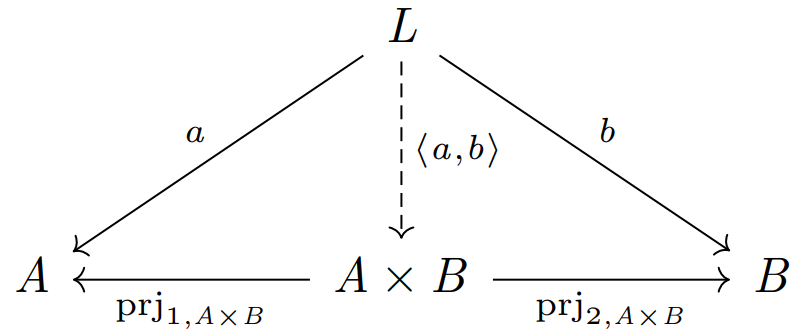
を可換にする一意的な射 \(L\rightarrow A\times B\) の存在を保証するような
- 対象 \(A\times B\)
- 射 \({\rm prj}_{1,A\times B}:A\times B\rightarrow A\)
- 射 \({\rm prj}_{2,A\times B}:A\times B\rightarrow B\)
という3つの射一式からなる構造であり、\(A\times B\) は積対象、\({\rm prj}_{1,A\times B}\) と \({\rm prj}_{2,A\times B}\) は 射影 (projection) と呼ばれる。
\(a,b\) に対して一意的に定まる射は、\(a,b\) によって引き起こされる射と呼ばれ、\(\langle a,b \rangle\) と書かれる。
入射で行った説明と同様の理由から、射影についても基本的にここでは \({\rm prj}_1, {\rm prj}_2\) というように型を省略した記号を使用する。
図式を使わずに、数式を直接用いてそのまま書くとするならば
\[
\begin{align}
a &= u_1 {\sf \, ⨟ \,} x \\
b &= u_2 {\sf \, ⨟ \,} x \\
\end{align}
\]
という関係式を満たす矢印 \(x:L\rightarrow A\times B\) が一意的に存在するという意味で、この条件はしばしば「積の普遍性」と呼ばれる。
余談
積についても「直積 (direct product)」という概念が nLab においては「圏論的積」とは異なるものとして定義されているという理由から、ここではそれらを区別する方針をとっている。
一階の言語による記述
射影であるために課される条件を2つの射が満たしているのかを判定する式
\[
{\rm arePrj}(p,q,X,A,B) :\Leftrightarrow \forall A \forall B[\forall f \forall g \forall L [(f:L\rightarrow A \wedge g:L\rightarrow B) \Rightarrow\exists ! h [h:L\rightarrow X \wedge {\rm \_comp}(h,p,f) \wedge {\rm \_comp}(h,q,g)]]]
\]
与えられた対象が積対象であるのかを判定する式
\[
{\rm isProdObj}(X,A,B) :\Leftrightarrow \exists p \exists q[{\rm arePrj}(p,q,X,A,B)]
\]
引き起こされた射であるのかを判定する式
\[
{\rm isParing}(h,f,g,p,q,X,A,B) :\Leftrightarrow {\rm arePrj}(p,q,X,A,B) \wedge {\rm \_comp}(h,p,f) \wedge {\rm \_comp}(h,q,g)
\]
積に関する重要な射の構成
射の積
\(f:A_1\rightarrow B_1\), \(g:A_2\rightarrow B_2\) を任意の射としたとき、次で定義される射 \((f\times g):A_1\times A_2 \rightarrow B_1\times B_2\) は \(f\) と \(g\) の積と呼ぶ。
\[
f\times g := \langle {\rm prj}_1 {\sf \, ⨟ \,} f, {\rm prj}_2 {\sf \, ⨟ \,} g \rangle
\]
対角射 (diagonal arrow)
次で定義される射 \(\Delta:A \rightarrow A\times A\) は対角射 (diagonal arrow)と呼ばれる。
\[
\Delta := \langle A,A \rangle
\]
余談
対角射 \(\Delta:A\rightarrow A\times A\) は(分裂)モニックであることが直ちに証明され、一般に \((A,\Delta)\) が積対象 \(A\times A\) の部分対象であることがいえる。
つまり \((A,\Delta) \subseteq (A \times A,{\rm id})\) が一般に満たされる。
つまり \((A,\Delta) \subseteq (A \times A,{\rm id})\) が一般に満たされる。
一般的抽象的ナンセンス
同じ対象からなる積対象同士の間には必ず同形射が存在する
\(A,B\) を対象とする。
もし圏が \(A,B\) の圏論的積 \((Z,p_1,p_2)\), \((Z',p_1',p_2')\) を持つと仮定すると、積の普遍性より
\[
\begin{align}
p_1 &= h {\sf \, ⨟ \,} p_1' \\
p_2 &= h {\sf \, ⨟ \,} p_2' \\
\\
p_1' &= h' {\sf \, ⨟ \,} p_1 \\
p_2' &= h' {\sf \, ⨟ \,} p_2 \\
\end{align}
\]
を満たす一意的な射 \(h:Z\rightarrow Z'\), \(h':Z'\rightarrow Z\) の存在が従う。
ここで、次の合成射
\[
\begin{align}
(h{\sf \, ⨟ \,} h') {\sf \, ⨟ \,} p_1 \\
(h{\sf \, ⨟ \,} h') {\sf \, ⨟ \,} p_2 \\
\end{align}
\]
を考えると
\[
\begin{align}
(h{\sf \, ⨟ \,} h') {\sf \, ⨟ \,} p_1 &= h{\sf \, ⨟ \,} (h' {\sf \, ⨟ \,} p_1) \\
&= h{\sf \, ⨟ \,} p_1' \\
&= p_1 \\
\\
(h{\sf \, ⨟ \,} h') {\sf \, ⨟ \,} p_2 &= h{\sf \, ⨟ \,} (h' {\sf \, ⨟ \,} p_2) \\
&= h{\sf \, ⨟ \,} p_2' \\
&= p_2 \\
\end{align}
\]
となる。
ここで、積の普遍性より
\[
\begin{align}
k {\sf \, ⨟ \,} p_1 &= p_1 \\
k {\sf \, ⨟ \,} p_2 &= p_2 \\
\end{align}
\]
を満たす \(k\) は一意に定まるわけだが、そのような関係を満たす既知の射として \(Z:Z\rightarrow Z\) が存在している。
つまり合成射 \((h{\sf \, ⨟ \,} h'):Z\rightarrow Z\) は \(Z:Z\rightarrow Z\) に限定される。
また同様の議論から、\((h'{\sf \, ⨟ \,} h):Z'\rightarrow Z'\) が \(Z':Z'\rightarrow Z'\) に限られることを示すこともできる。
よって
\[
\begin{align}
h{\sf \, ⨟ \,} h' &= Z \\
h'{\sf \, ⨟ \,} h &= Z' \\
\end{align}
\]
が成り立つため、\(Z\cong Z'\) となる。
余談
このように積対象同士は同形であるため、点 (対象) だけを見比べるとそれらの間に一切の違いを見出すことはできない。とはいえ、「圏論的積」というのは「2つの射影の構造が一緒に指定されていて初めて一つの完成形」であり、その一式同士で比べれば、圏論的積の間にも意味合いの違いは生じてくる。
例えば典型的なのは \(A\times B \cong B\times A\) が成り立つため、対象レベルで見ればそれら \(A\times B\) と \(B\times A\) を区別することはできないが、「積という構造一式」で見た場合、\(A\) と \(B\) の積対象 \(A\times B\) の持つ第一射影と\(B\) と \(A\) の積対象 \(B\times A\) の持つ第一射影は明らかに異なる。
双対性
(...)
タグ一覧: