雑記帳
直和 (direct sum) と弱直積 (weak direct product)

目次
直和 (direct sum)
注意点
しばしば余積 (coproduct) のことが直和と訳される場合がある。
例えば 2023/1/2 現在、日本語版 Wikipedia においては以下のように説明されている。
圏論における直和(英: coproduct; 余積、双対直積)とは、直積 (product) の双対概念で、次の普遍性を持つ対象 A のことである ... (以下省略)
このように異なる概念に対して重複する日本語が割り当てられているため少しわかりづらいかもしれないが、このページで説明する直和は「coproduct」ではなく「direct sum」のことを指している。
また、このページだけに限らず、このノート全体では
- 「coproduct」の日本語訳は「余積」
- 「direct sum」の日本語訳は「直和」
といった区別をしていくため、混同しないように注意してほしい。
因みに「直和と余積を別概念として扱う」というのは僕の勝手な独断によるものではなく、以下のページ
- direct sum (nLab 記事)
の流儀に倣っているだけである。実際このページの情報は上のリンク先の記事の単なる日本語訳のようなものに過ぎない。
導入
直積 vs 直和

線形代数の教科書等を色々と読んでみれば自ずと感じることであるとは思うが、通常「直和に対する、任意の数学的構造に共通した一般的抽象的な概念的定義」というものは説明されない場合が多い。
例えば、ある教科書では \(A\) と \(B\) の直和 (抽象的な直和) とは
- \(A\) と \(B\) のそれぞれの基底集合の積に、\(A\), \(B\) の持つ演算構造から誘導される成分同士の加法とスカラー倍を指定することで得られる線形空間
と定義したり、\(\langle A, i_A\rangle\), \(\langle B, i_B\rangle\) をある線形空間 \(V\) の部分線形空間としたとき、
- それら部分空間の持つ構造である包含を介して \(V\) 上に持って行った任意のベクトル同士を \(V\) の持つ加法を使って足し合わせることで得られるベクトル全体からなる \(V\) の部分線形空間の内、\(A,B\) の基底集合と、\(V\) の基底集合 \(U(V)\) へのモニック射から得られる2つの \(U(V)\) の部分集合同士の積 (つまり共通部分) が \({\rm Sub}(U(V))\) の始対象となるようなもの
を直和 (部分空間としての直和) と定義したりする。
余談
そのようにして得られる「2つの部分空間のベクトルの和が張る部分線形空間」はしばしば和空間と呼ばれ \(A+B\) と表記されるが、圏論的に考える場合「線形空間」と「部分線形空間」は異なる構造であり、「\(A+B\) は線形空間の圏における余積」、「\(\langle A, i_A\rangle+\langle B, i_B\rangle\) は \(V\) の部分空間のなす圏における余積」というように区別される。
そういった事情もあり、実際直和に対して
- 基本的には「直積」と同じものだが、非有限族の直和の場合においては例外的に少し異なった構成になってしまうという、結局のところよくわからない子
といった程度の認識で済ませておかなければならない "モヤモヤの残る概念" というイメージが植え付いている人も少なからずいると思う。
例えば、こういった認識だと
- 「直和」と「直積」の間に具体的にどういった意味の違いが存在しているのか?
といった疑問にスパっと答えることが難しい。これについて
- 「有限個の成分を持つタプル (と見做せる族)」だけをちょうど持つ直積の一部分として得られる直積の部分空間が直和
という回答もできそうではあるが、「つまるところそれが何を意味していて、どういったうれしさがあるのか」という点がなかなか見えてこないし、(線形空間やアーベル群等に限定することなく一般的に考える場合) 何ゆえ "和 (sum)" という言葉が名称に含まれているのかという部分も明らかにならない。
圏論の言葉を使えば、「直和」の概念は余積や積などと同様、一般的抽象的に定義することができる。
この見方をすれば「どうして有限でなければいけないのか」という部分も、
- 「部分空間としての直和」を非有限族に対して考えたいとき、「任意有限回の加法」は可能であっても「無限回の加法」という操作は一般の線形空間が認める操作ではないわけなので、「抽象的な直和」の場合においても、その点を同様に考慮するのは当然でしょう。
というような数学的構造の持つ演算側の都合寄りなものではなく、もっと初等的に物事を捉えることが可能になる。
また興味深いことに、上で説明したような「有限個の成分を持つタプルからなる直積の部分空間」としての直和の構成は、圏論的な立場からは「直和」ではなく「弱直積」と呼ばれる別の意味を持った構成であることが明らかになる。
後でまた例として紹介するが、「弱直積」は文字通り「積」であり、有限の場合は「(圏論的)積」そのものになるため、どの数学的構造においても「直積」と「弱直積」の間に違いは生まれない。
一方で直和の場合、以下に述べる定義からもわかるように「(圏論的)和」との繋がりがしっかりとあり、有限の場合でも直積と直和の間に意味の違いが生じるパターンもある。
具体的には、群やアーベル群の場合は \(A\oplus B\) と \(A\times B\) が同形になり、従来の「直和が直積と同じに見える」という状況を得ることができるが、点付き集合の場合、\(A\oplus B\) は \(A+B\) と同形になり、直和は直積それ自体とは異なった性質を持つことになる。
定義
2つの対象 A,B の直和 A⊕B
全ての余積と積を持ち、さらにゼロ対象を持つような正則圏において、2つの対象 \(A,B\) が与えられたとき、\(A\) と \(B\) の直和 (direct sum) とは、
\[
{\rm inj}_k {\sf \, ⨟ \,} r {\sf \, ⨟ \,} {\rm prj}_l =
\begin{cases}
{\rm id} & \text{ if } k=l \\
0 & \text{ if } k\ne l
\end{cases}
\]
という関係式を満たすことになる
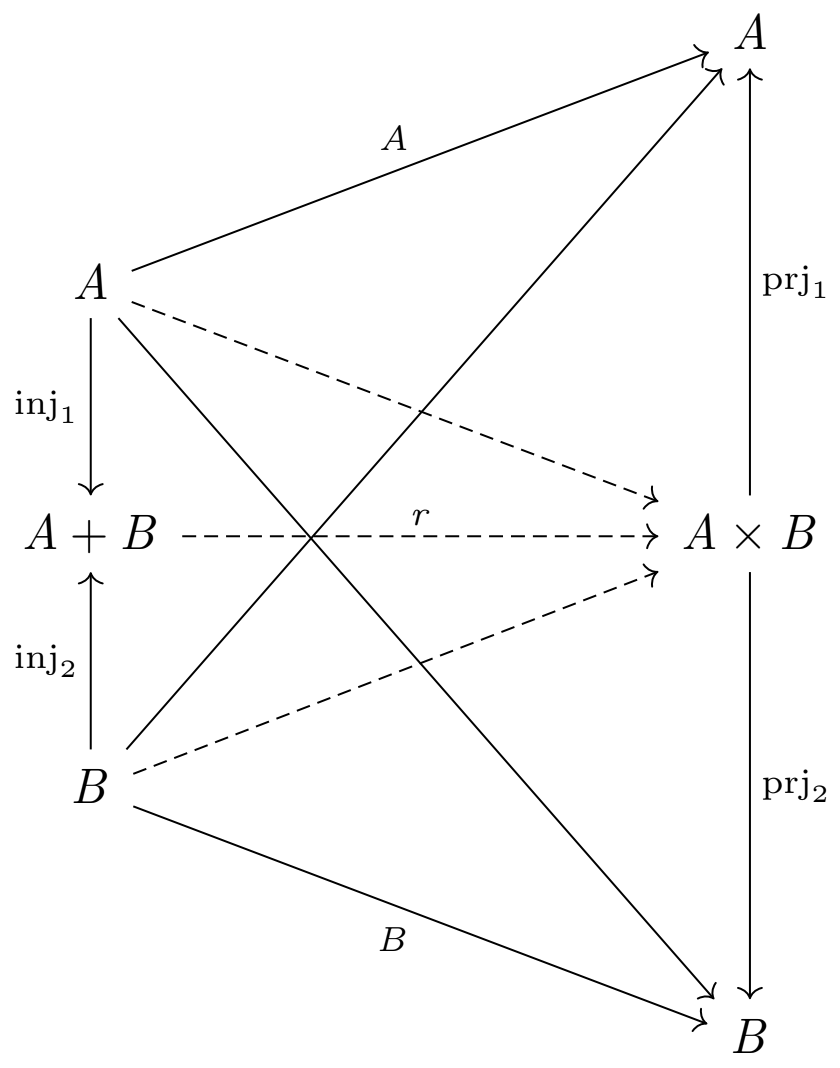
\[
r = \left(
\matrix{\langle A,0 \rangle \cr \langle 0,B \rangle }
\right)
\]
として構成される射 \(r\) の像として定義される。
語弊のないように言い換えると、
\[
r = r|^S {\sf \, ⨟ \,} i_S
\]
を満足する任意の射 \(r|^S:A+B\rightarrow S\) とモニック射 \(i_S:S\rightarrow A\times B\) について、以下の図式
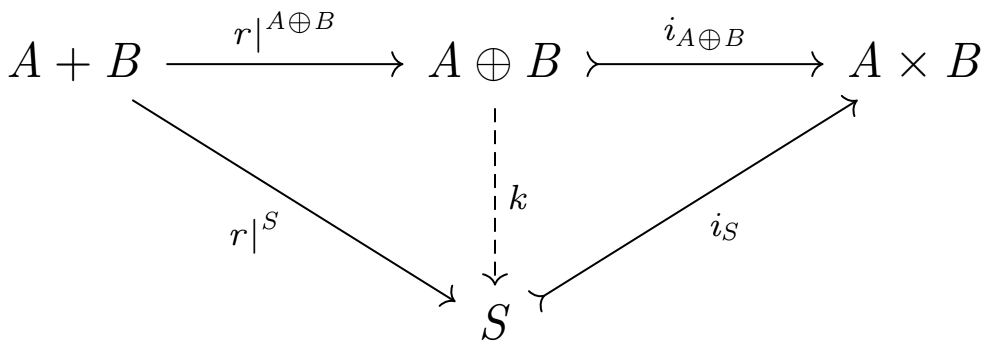
を可換にする射 \(k:A\oplus B \rightarrow S\) の存在を保証する (因みに、この射は一般的抽象的ナンセンスより存在すれば一意に定まる) ような
- 対象 \(A\oplus B\)
- 射 \(r|^{A\oplus B}:A+B\rightarrow A\oplus B\)
- モニック射 \(i_{A\oplus B}:A\oplus B\rightarrow A\times B\)
という3つの射一式からなる構造である。
ここで現在、正則圏を仮定しているためその圏が押し出しを持つ (余核対の構成が任意にできる) 場合、その像は \(r\) の余核対のイコライザとして構成される。
また、上の図式を見ればわかるが、最後に余積対象からの射を生やすために用いている射のペアリングは特定の射影をレトラクションとして持つ。つまりそれら全ての射は \(A\times B\) をコドメインにとる分裂モニックであり、それぞれ \(A\times B\) の部分対象を成す。
余談
この定義において、ゼロ対象を持たない集合の圏では「直和」の構成はできないため「集合 \(A,B\) の余積 \(A+B\) (これを「集合の直和」と呼ぶ文献も存在する)」は考えることはできても「集合 \(A,B\) の直和 \(A\oplus B\)」という概念を厳密には考えることができない。
とはいえ、\({\mathbb{N}}\) を始めとする \(X_n\cong X_n+1\) を満たす対象 \(X_n\) (その同形を与える適当な同形射を \(i_{X_n}:X_n\rightarrow X_n+1\) と置く) に対しては、\(!{\sf \, ⨟ \,} {\rm inj}_2 {\sf \, ⨟ \,} {i_{X_m}}^{-1}\) という形でゼロ射のような射 \(0:X_n\rightarrow X_m\) を構成でき、それを用いて上で説明した意味での直和に相当する構成を行うことは可能である。
対象の族の直和
\(\mathscr{C}\) を全ての余積と積を持ち、さらにゼロ対象を持つような正則圏とする。
ここで、
- \(\mathscr{C}_0\): 圏 \(\mathscr{C}\) の対象全体の空間として与えている ∞-亜群
- \(I\): 0-亜群
- \(A:I\rightarrow \mathscr{C}_0\): 圏 \(\mathscr{C}\) の対象の族
とすると、(\(I\) が決定可能な相等関係を持つ場合) 余積と積の普遍性から、先に登場した以下の条件式を満たすような射 \(r\) を構成することができる。
\[
{\rm inj}_k {\sf \, ⨟ \,} r {\sf \, ⨟ \,} {\rm prj}_l =
\begin{cases}
{\rm id} & \text{ if } k=l \\
0 & \text{ if } k\ne l
\end{cases}
\]
このとき、\(r\) の像 \(\langle {\rm im}\,r , j \rangle\) として定義される部分対象のことを 「対象の族 \(A:I\rightarrow \mathscr{C}_0\) の直和 (direct sum)」と呼び、その対象 \({\rm im}\,r\) を
\[
\bigoplus_{i:I} A_i
\]
という記号で表す。
先ほど説明した「2つの対象 \(A,B\) の直和 \(A\oplus B\)」は、この定義からは、「\(I\) が濃度2の集合である場合における、対象の族の直和」に該当する。
また \(I\) が有限濃度の場合は、その際に紹介した射 \(r\) の構成方法と変わらない方法によって構成することができる。
例えば、濃度が3の場合は、
\[
r = \left(
\matrix{\langle A_1,0,0 \rangle \cr \langle 0,A_2,0 \rangle \cr \langle 0,0,A_3 \rangle }
\right)
\]
として構成される。
例
直和は、考える圏によってどういった性質を持った対象になるのかがまちまちとなっていて、「直和は、余積と同形である」とか「直和は、積と同形である」といった主張は一概にできない。
その様子を具体例から確認してみていってほしい。
アーベル群の直和
アーベル群の圏のような
- 双積 (biproduct): \(A,B\) を圏の対象としたとき、\(A\) と \(B\) の余積と積の普遍性を同時に満足するような対象
を持つ圏においては、積対象 \(A\times B\) の要素全体が余積対象としての性質を持つことになるため、その積対象全体が直和になる。より一般に、双積を持つ圏において、直和 \(\langle A\oplus B, i_{A\oplus B} \rangle\) はその親となる部分対象である \(\langle A\times B, {\rm id} \rangle\) と圏 \({\rm Sub}(A\times B)\) の対象として同形になる。但し、有限族でない族 \(I\) の直和になると、必ずしも積全体が直和になるとは云えなくなる。
わかりやすく纏めると、この圏では
- \(A\oplus B\) は \(A + B\) と一般に同形である
- \(A\oplus B\) は \(A\times B\) とも一般に同形である
といった状況になっている。(もちろん対象の非有限族の直和の場合は、\(r\) の構成方法を「有限族で通用する方法」の延長上で考えることは出来ないため、この帰結も非有限族の場合には適用されない。)
点付き集合の直和
点付き集合の圏における対象 \(A\) と \(B\) の直和は、 \(A\times B\) の部分対象として見たウェッジ和 \(A+B\) そのものになる。
わかりやすく纏めると、この圏では
- \(A\oplus B\) は \(A + B\) と一般に同形である
- \(A\oplus B\) は \(A\times B\) と一般に同形でない
といった状況になっている。
群の直和
群の圏においても、余積と積は大きく異なるにも関わらず、2つの対象の直和 \(\langle A\oplus B, i_{A\oplus B} \rangle\) はその親となる部分対象である \(\langle A\times B, {\rm id} \rangle\) と圏 \({\rm Sub}(A\times B)\) の対象として同形になることが知られている。(もし余積対象が積対象にすっぽり収まりきれていれば、点付き集合の場合と同様、余積そのものが直和となるが、実際そうなっていないことからも、群の余積という構成によって得られる群が少なくとも積として得られる群よりも巨大であることがイメージできるのではないだろうか。)
わかりやすく纏めると、この圏では
- \(A\oplus B\) は \(A + B\) と一般に同形でない
- \(A\oplus B\) は \(A\times B\) と一般に同形である
といった状況になっている。
特に非有限族になると、この圏における直和は「余積でも積でもない対象」となる場合もある。
弱直積 (weak direct product)
(...)
タグ一覧:
