圏を一階述語論理で公理化する

より具体的には、対象間の「同じである」という情報が既に組み込まれている「亜群」という構造の上から「不可逆な射をも含めた射のレイヤー」を適切に重ね合わせることで、「同じである」以外にも、どの対象群がどういった特別な意味を持つ空間群であるのかをラベル付けたり、数学的構造の一つとしてどういった特別な性質を持ち得るのかを明らかにしたりする。この時、新たに重ねたレイヤー上で定まる「対象が同じであること」と元々の亜群が持っている「対象が同じであること」は同じ意味でなければならない。)

そのレイヤーが重ねられる構造として使用している「亜群」の代わりに「集合 (ホモトピー0型)」を使ってはいけないのかと疑問に思うかもしれないが、許容自体はされているものの、その種類の圏は「Strict 圏」と呼ばれ、「数学的構造の対象を研究するためのフレームワーク」という用途には向かない。

実際、集合や群を始めとする数学的構造の対象を集めた空間というのは (ホモトピー型理論の土台の上では) どうしても「亜群」になってしまう。(数学的構造の対象全体の "集合" なんてものを一般に構成できない。)

この観点からは、圏というのは「数学的構造の対象を抽象的に取り扱うための便利な枠組み」という見方ができる。

「Strict 圏」の観点から

集合 (点の集まり) 内の点同士の間に矢印を組み込んで得られる有向グラフの内、矢印同士の間の合成演算が矛盾なく定義されているもの。

この観点からは、圏は「群に似た数学的構造の一種」という見方ができる。

「Dagger 圏」の観点から

(..)

フォーマルな定義 (single-sorted 一階述語論理 ver.)

このノートでも Saunders Mac Lane の有名な圏論の教科書 (CWM: Categories for the Working Mathematician / 圏論の基礎) と同様、まずは圏を公理的に定義する。

(hom 集合を用いたより理想的な圏の定義は、ホモトピー型理論を基礎として導入した後にまた改めて説明する。)

ちなみに本来であれば、「対象」と「射」を分けて圏を定義する方が自然であるのだが、以下の点を考慮して敢えて single-sorted の公理化を採用することにする。

Lawvere の ETCS の論文で採用されている圏の公理化と準拠する公理化 (例えば論文内でもドメイン・コドメインはそれぞれ二項述語、合成は三項述語という形の未定義述語として与えた single-sorted の一階の理論として圏を公理化している) を採用することで、ここでも「\(A:A\rightarrow A\)」という記号を表記の濫用ではなく、厳密に正しい記号として使用できるようにする。
一階の言語で記述するとなった時、やはり single-sorted の方がシンプルに書ける気がする。特に一番理想的な「hom 集合を用いた定義」の場合、集合の概念が圏よりも先行して与えられている必要があるため、一階述語論理でそのスタイルの圏の公理化を行うことは技術的に難しい。
single-sorted で公理化される ZFC と同じく single-sorted で公理化しておくことで、後に登場する圏論的な公理的集合論である ETCS と ZFC との比較をフェアにできるようにする。
対象が根源的であることを強調する。(対象それ自体が「中身 (content)」を何も持たないことを理解しやすくする。)

射のドメイン・コドメインの公理

\[ \begin{align*} &\forall f[\exists h[{\rm \_dom}(f,h) \wedge \forall i[{\rm \_dom}(f,i) \Rightarrow (h=i)]]]\\ &\forall f[\exists h[{\rm \_cod}(f,h) \wedge \forall i[{\rm \_cod}(f,i) \Rightarrow (h=i)]]]\\ &\forall f \forall h[{\rm \_dom}(f,h) \Rightarrow ({\rm \_dom}(h,h) \wedge {\rm \_cod}(h,h))]\\ &\forall f \forall h[{\rm \_cod}(f,h) \Rightarrow ({\rm \_cod}(h,h) \wedge {\rm \_dom}(h,h))]\\ \end{align*} \]

合成射の公理

\[ \begin{align*} &\forall f \forall g[ \exists i[{\rm \_cod}(f,i) \wedge {\rm \_dom}(g,i)] \Rightarrow \exists h[{\rm \_comp}(f,g,h) \wedge \forall j[{\rm \_comp}(f,g,j) \Rightarrow j=h]]]\\ &\forall f \forall g \forall h[{\rm \_comp}(f,g,h) \Rightarrow ( \exists i[{\rm \_cod}(f,i) \wedge {\rm \_dom}(g,i)] \wedge ( \exists i[{\rm \_dom}(h,i) \wedge {\rm \_dom}(f,i)] \wedge \exists i[{\rm \_cod}(h,i) \wedge {\rm \_cod}(g,i)]))]\\ \end{align*} \]

恒等射の公理

\[ \begin{align*} \forall f[ \forall h[{\rm \_dom}(f,h) \Rightarrow {\rm \_comp}(h,f,f)] \wedge \forall h[{\rm \_cod}(f,h) \Rightarrow {\rm \_comp}(f,h,f)]]\\ \end{align*} \]

合成射の結合性公理

\[ \begin{align*} \forall f \forall g \forall h \forall j \forall k \forall m[{\rm \_comp}(f,g,j) \wedge {\rm \_comp}(g,h,k) \Rightarrow ({\rm \_comp}(j,h,m) \Leftrightarrow {\rm \_comp}(f,k,m))]\\ \end{align*} \]

余談

このようにして公理的に定義される圏は、CWM ではメタ圏 (metacategory) と呼ばれている。

定義の読み解き

先ほど一階述語論理の言葉を用いた圏の公理化を書き下したが、少しわかりにくい可能性があるので補足しておく。

まずわかりやすくなるように以下の略記を導入する。

\[ f:X\rightarrow Y :\Leftrightarrow ({\rm \_dom}(f,X) \wedge {\rm \_cod}(f,Y)) \]

(ちなみにこの略記は今後も頻繁に使用していく)

射のドメイン・コドメインの公理

任意の射 \(f\) にその射のドメインと呼ばれる一意的な射が割り当てられる。(その一意的な射は \({\rm dom}(f)\) と表記される。)
任意の射 \(f\) にその射のコドメインと呼ばれる一意的な射が割り当てられる。(その一意的な射は \({\rm cod}(f)\) と表記される。)
ドメイン・コドメインの割り当ては冪等 (idempotent)である。(つまりドメイン或いはコドメインとして割り当てている射のドメイン・コドメインはそれ自身を定める。)

つまりは \(f\) を射としたとき、\(f:X\rightarrow Y\) と書けるような \(X,Y\) が一意的に定まるということと、\(f:X\rightarrow Y\) であるとき、\(X:X\rightarrow X\) かつ \(Y:Y\rightarrow Y\) であるということを云っている。(またドメイン・コドメインとして割り当てられる射を、今後しばしば「対象 (object)」と呼ぶ。)

合成射の公理

射 \(f,g\) について、\(f\) のコドメインと \(g\) のドメインが共通であるとき、それらは合成可能であり、それらの合成射 \(h\) は一意的に定まる。(その一意的な射は \(f {\sf \, ⨟ \,} g\) または \(g \circ f\) と表記される。)
射 \(f,g\) が合成可能でその合成射が \(h\) であるとき、\(f\) のコドメインと \(g\) のドメインは共通かつ、その合成射 \(h\) のドメインは \(f\) のドメイン、コドメインは \(g\) のコドメインとそれぞれ共通している。

つまり、射 \(f:X\rightarrow Y\), \(g:Y\rightarrow Z\) が与えられたとき、それらは合成可能であり、その合成射は何らかの一意的な射 \((f{\sf \, ⨟ \,} g):X\rightarrow Z\) として割り当てられるということと、\(f\) と \(g\) の合成射 \((f{\sf \, ⨟ \,} g):A\rightarrow B\) が与えられるとき、\(f,g\) はある射 \(X\) があってそれぞれ \(f:A\rightarrow X\), \(g:X\rightarrow B\) とそれぞれ書かれるということを云っている。

恒等射の公理

ドメイン・コドメインとして割り当てる射は、射の合成に関して自明に振舞う。

つまり、射 \(f:X\rightarrow Y\) が与えられたとき、\(X {\sf \, ⨟ \,} f = f\) と \(f {\sf \, ⨟ \,} Y = f\) が常に成り立つ。(この公理化の下では対象 \(X\) は \(X:X\rightarrow X\) を満たす自明な振舞いをする射として扱われるのだが、そのような射は従来の圏の定義の中では「恒等射 (identity arrow)」と呼ばれる射に該当する。実際「対象」と呼ぶより「恒等射」と呼んだ方がわかりやすくなる場面も多いので、今後対象を恒等射の意味合いで用いていることを明示したい時のために \({\rm id}_X := X\) という記号を定義しておく。)

合成射の結合性公理

射の合成射の割り当ては結合的である。

つまり、\((f {\sf \, ⨟ \,} g) {\sf \, ⨟ \,} h = f {\sf \, ⨟ \,} (g {\sf \, ⨟ \,} h)\) が常に成り立つ。(その一意的な射は \(f {\sf \, ⨟ \,} g {\sf \, ⨟ \,} h\) と表記される。)

余談

公理的に圏を扱う場合、「function application (関数に対する値の適用?)」は射の合成が担うことになる。

例えば \(g(f(x))\) と \((g\circ f)(x)\) はそれぞれ \((x {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g\) と \(x {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g)\) に対応することになるのだが、見ての通り値と関数を切り離すためにも射の結合性が重要な役割を果たすことになる。

圏の公理を満たす理論の例

まず注意点を挙げておくと、「圏の公理を満たす理論 (以下に挙げるような圏の examples)」と「特定の公理を課した圏の一般論を行う舞台 (圏の公理系, トポスの公理系, ETCS 集合論の公理系)」とを混同しないように注意してほしい。
後者は「その公理系を満たす任意の理論に並行して行われる一般論を展開する枠組み」であり、前者は「圏の公理系を満たす理論の例」つまり「圏の一般論が適用可能な具体的な理論」である。

ETCS を公理化する際にも再度同じことを注意喚起すると思うが、ETCS は ZFC 同様あくまで「集合の公理系」であり、ETCS の場合は圏の "一種" であっても「具体的な一つの圏」を一般に定めない。つまり、例えば ETCS や ZFC のモデルを作ったときに、公理系に含めていない情報 (ETCS の場合: 具体圏か否か等、ZFC の場合: 連続体仮説が成立するか否かなど) が入り込む隙が残っている。(もちろんある圏を構成したとき、その圏が ETCS 公理系を満たしていれば、それは ETCS 公理系を満たす「具体的な一つの圏」ではある。よりわかりやすい例を挙げると、以下に挙げる「終圏」はトポスの公理を満たすことになるため「具体的な一つのトポス」である一方、「トポス」それ自体は圏の種類であって「具体的な一つの圏」を意味していない。)

空圏 (empty category)

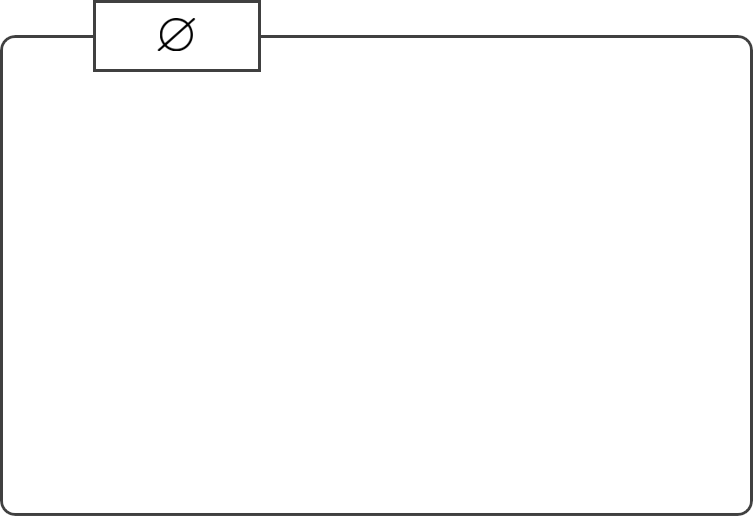
以下の3つの公理からなる一階の理論は圏をなす。この圏は空圏 (empty category) と呼ばれ、\(\varnothing\) や \(\mathbf{0}\) といった記号で表す。

\({\rm \_dom}, {\rm \_cod}\): binary 述語
\({\rm \_comp}\): ternary 述語

\[ \begin{align} &\forall f \forall h[\neg({\rm \_dom}(f,h))] \\ &\forall f \forall h[\neg({\rm \_cod}(f,h))] \\ &\forall f \forall g \forall h[\neg({\rm \_comp}(f,g,h))] \\ \end{align} \]

Haskell を使ってこのデータ群が圏の公理を全て満たすかを確認すると以下のように True を返す

ghci> check_if_it's_a_category (listOfData :: [EmptyCat])
isCategory: True
Details: [True,True,True,True,True,True,True,True]

終圏 (terminal category)

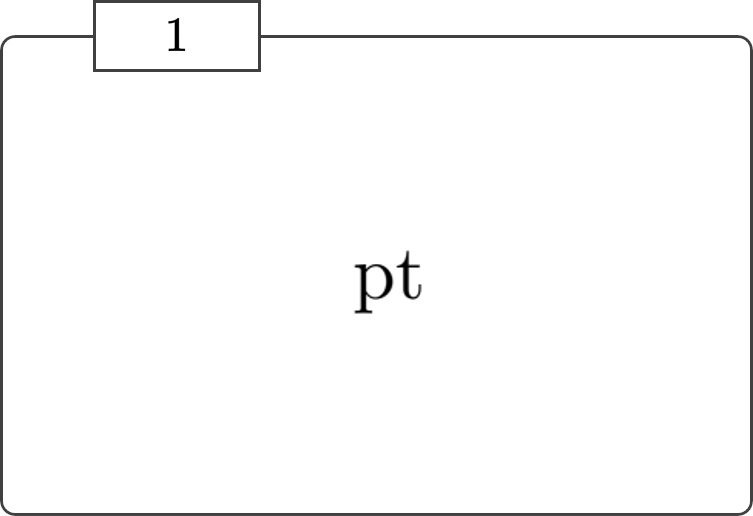
以下の4つの公理からなる一階の理論は圏をなす。この圏は終圏 (terminal category / final category) や自明な圏 (trivial category) などとと呼ばれ、\(1\) または \(\mathbf{1}\) などといった記号で表す。

\({\rm \_dom}, {\rm \_cod}\): binary 述語
\({\rm \_comp}\): ternary 述語
\({\rm pt}\): nullary 関数記号

\[ \begin{align} &\forall h[h={\rm pt}] \\ &{\rm \_dom}({\rm pt},{\rm pt}) \\ &{\rm \_cod}({\rm pt},{\rm pt}) \\ &{\rm \_comp}({\rm pt},{\rm pt},{\rm pt}) \\ \end{align} \]

見方を変えれば

\[ \begin{align} &\forall h[h={\rm pt}] \\ &\forall f \forall h[{\rm \_dom}(f,h)] \\ &\forall f \forall h[{\rm \_cod}(f,h)] \\ &\forall f \forall g \forall h[{\rm \_comp}(f,g,h)] \\ \end{align} \]

ちなみに、関数記号を使うことを避けたいのであれば、\({\rm pt}\) を述語 \({\rm pt}(h)\) に置き換えて

\[ \begin{align} &\exists p[{\rm pt}(p) \wedge \forall h[{\rm pt}(h) \Rightarrow h=p]] \\ &\forall p[{\rm pt}(p) \Rightarrow (\forall h[h=p])] \\ &\forall p[{\rm pt}(p) \Rightarrow ({\rm \_dom}(p,p))] \\ &\forall p[{\rm pt}(p) \Rightarrow ({\rm \_cod}(p,p))] \\ &\forall p[{\rm pt}(p) \Rightarrow ({\rm \_comp}(p,p,p))] \\ \end{align} \]

というように公理化することもできる。

Haskell を使ってこのデータ群が圏の公理を全て満たすかを確認すると以下のように True を返す

ghci> check_if_it's_a_category (listOfData :: [TerminalCat])
isCategory: True
Details: [True,True,True,True,True,True,True,True]

異なる2点からなる離散圏

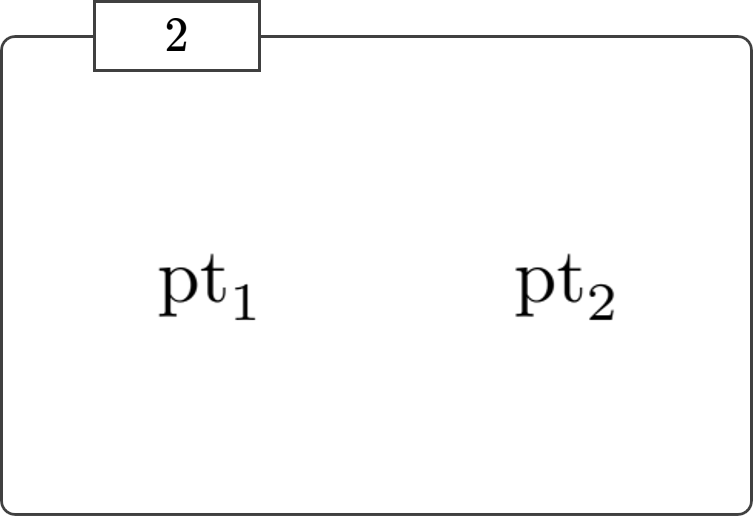
以下の公理からなる一階の理論は圏をなす。(ここではその圏を \(2\) とラベル付けることにする。)

\({\rm \_dom}, {\rm \_cod}\): binary 述語
\({\rm \_comp}\): ternary 述語
\({\rm pt}_1,{\rm pt}_2\): nullary 関数記号

\[ \begin{align} &\forall h[h={\rm pt}_1 \vee h={\rm pt}_2] \\ &{\rm \_dom}({\rm pt}_1,{\rm pt}_1) \\ &{\rm \_cod}({\rm pt}_1,{\rm pt}_1) \\ &{\rm \_comp}({\rm pt}_1,{\rm pt}_1,{\rm pt}_1) \\ &{\rm \_dom}({\rm pt}_2,{\rm pt}_2) \\ &{\rm \_cod}({\rm pt}_2,{\rm pt}_2) \\ &{\rm \_comp}({\rm pt}_2,{\rm pt}_2,{\rm pt}_2) \\ &\neg({\rm \_dom}({\rm pt}_1,{\rm pt}_2)) \\ &\neg({\rm \_dom}({\rm pt}_2,{\rm pt}_1)) \\ &\neg({\rm \_cod}({\rm pt}_1,{\rm pt}_2)) \\ &\neg({\rm \_cod}({\rm pt}_2,{\rm pt}_1)) \\ &\neg({\rm \_comp}({\rm pt}_1,{\rm pt}_1,{\rm pt}_2)) \\ &\neg({\rm \_comp}({\rm pt}_1,{\rm pt}_2,{\rm pt}_1)) \\ &\neg({\rm \_comp}({\rm pt}_1,{\rm pt}_2,{\rm pt}_2)) \\ &\neg({\rm \_comp}({\rm pt}_2,{\rm pt}_1,{\rm pt}_1)) \\ &\neg({\rm \_comp}({\rm pt}_2,{\rm pt}_1,{\rm pt}_1)) \\ &\neg({\rm \_comp}({\rm pt}_2,{\rm pt}_1,{\rm pt}_1)) \\ &\neg({\rm \_comp}({\rm pt}_2,{\rm pt}_1,{\rm pt}_2)) \\ &\neg({\rm \_comp}({\rm pt}_2,{\rm pt}_2,{\rm pt}_1)) \\ \end{align} \]

区間圏 (interval category)

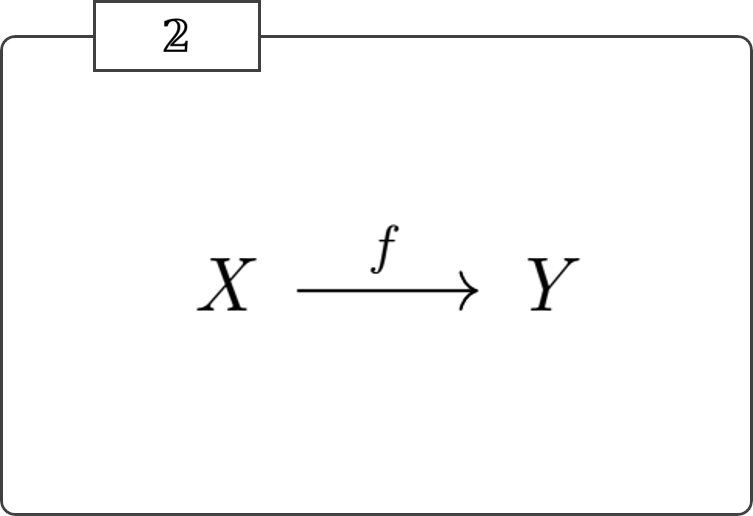
以下の公理からなる一階の理論として、具体的な有限の有向グラフの形をした圏が得られる。この圏は区間圏 (interval category) と呼ばれ、\(\mathbb{2}\) または \((\cdot \rightarrow \cdot)\) などといった記号で表す。

\({\rm \_dom}, {\rm \_cod}\): binary 述語
\({\rm \_comp}\): ternary 述語
\(X,Y,f\): nullary 関数記号

\[ \begin{align} &\forall h[h=X \vee h=Y \vee h=f] \\ &{\rm \_dom}(X,X) \\ &\neg({\rm \_dom}(Y,X)) \\ &{\rm \_dom}(f,X) \\ &\neg({\rm \_dom}(X,Y)) \\ &{\rm \_dom}(Y,Y) \\ &\neg({\rm \_dom}(f,Y)) \\ &\neg({\rm \_dom}(X,f)) \\ &\neg({\rm \_dom}(Y,f)) \\ &\neg({\rm \_dom}(Z,f)) \\ &{\rm \_cod}(X,X) \\ &\neg({\rm \_cod}(Y,X)) \\ &\neg({\rm \_cod}(f,X)) \\ &\neg({\rm \_cod}(X,Y)) \\ &{\rm \_cod}(Y,Y) \\ &{\rm \_cod}(f,Y) \\ &\neg({\rm \_cod}(X,f)) \\ &\neg({\rm \_cod}(Y,f)) \\ &\neg({\rm \_cod}(Z,f)) \\ &{\rm \_comp}(X,X,X) \\ &\neg({\rm \_comp}(X,X,Y)) \\ &\neg({\rm \_comp}(X,X,f)) \\ &\neg({\rm \_comp}(X,Y,X)) \\ &\neg({\rm \_comp}(X,Y,Y)) \\ &\neg({\rm \_comp}(X,Y,f)) \\ &\neg({\rm \_comp}(X,f,X)) \\ &\neg({\rm \_comp}(X,f,Y)) \\ &{\rm \_comp}(X,f,f) \\ &\neg({\rm \_comp}(Y,X,X)) \\ &\neg({\rm \_comp}(Y,X,Y)) \\ &\neg({\rm \_comp}(Y,X,f)) \\ &\neg({\rm \_comp}(Y,Y,X)) \\ &{\rm \_comp}(Y,Y,Y) \\ &\neg({\rm \_comp}(Y,Y,f)) \\ &\neg({\rm \_comp}(Y,f,X)) \\ &\neg({\rm \_comp}(Y,f,Y)) \\ &\neg({\rm \_comp}(Y,f,f)) \\ &\neg({\rm \_comp}(f,X,X)) \\ &\neg({\rm \_comp}(f,X,Y)) \\ &\neg({\rm \_comp}(f,X,f)) \\ &\neg({\rm \_comp}(f,Y,X)) \\ &\neg({\rm \_comp}(f,Y,Y)) \\ &{\rm \_comp}(f,Y,f) \\ &\neg({\rm \_comp}(f,f,X)) \\ &\neg({\rm \_comp}(f,f,Y)) \\ &\neg({\rm \_comp}(f,f,f)) \\ \end{align} \]

(有限グラフからなる圏は技術的には全てのパターンに対する真偽を愚直に書き並べることで、圏である一階の理論として書き下すことができるが、射の総数が増えてくると非常に長くなってしまうため以降は省略し、圏の全体像となる有向グラフと合成の規則だけを示すだけにさせてもらう。)

異なる3点からなる半順序

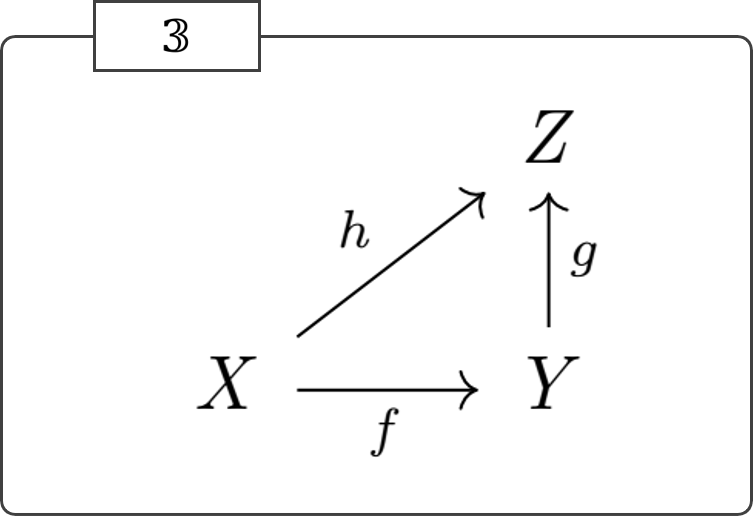
以下のように合成の規則を与えた矢印たちは圏をなす。(ここではその圏を \(\mathbb{3}\) とラベル付けることにする。)

\[ \begin{align} X {\sf \, ⨟ \,} X &:= X \\ Y {\sf \, ⨟ \,} Y &:= Y \\ Z {\sf \, ⨟ \,} Z &:= Z \\ &\\ X {\sf \, ⨟ \,} f &:= f \\ f {\sf \, ⨟ \,} Y &:= f \\ &\\ Y {\sf \, ⨟ \,} g &:= g \\ g {\sf \, ⨟ \,} Z &:= g \\ &\\ X {\sf \, ⨟ \,} h &:= h \\ h {\sf \, ⨟ \,} Z &:= h \\ &\\ f {\sf \, ⨟ \,} g &:= h \\ \end{align} \]

余談

この圏はしばしば「圏論のある種のアイコン」として使用されるため敢えて強調しておくが、上の図は「圏 \(\mathbb{3}\) の有向グラフとしての形」(CWM でいうところのメタグラフ) である。

\(X,Y,f\) といった紛らわしい記号を使っていることもあってか、実際その図に対して「単に2つの写像を合成している様子を描いた図」(あるいは「図式 (ある周囲圏の持つ射を用いて作った有向グラフ)」) というような見方をとることもできてしまうわけであるが、その種の見間違いをしないように気を付けてほしい。

その図は、圏という一つの完成形であり、「対象 \(X\) の (物質的集合論的な意味での) 要素とは何なのか？」を始めとする、その圏の中にそもそもとして居ない住人を探し求める行為はナンセンスである。(関手 \(\mathbb{3} \rightarrow \mathbf{Set}\) を使ってこの圏を集合の圏 \(\mathbf{Set}\) に埋め込めば、この圏のそれぞれの対象が集合の圏の対象と結びつけられ、集合の圏の中で要素の概念を考えることはできるようになるが、埋め込んだ先の対象と埋め込む前の対象は一般に同じではない。)

Haskell を使ってこのデータ群が圏の公理を全て満たすかを確認すると以下のように True を返す

ghci> check_if_it's_a_category (listOfData :: [Cat_B3])
isCategory: True
Details: [True,True,True,True,True,True,True,True]

ちなみに射 \(h\) を取り除いた場合、\(f\) と \(g\) の合成射を割り当てられないため圏を成さない。実際にそのようなデータ群を作って圏の公理を満たすかを確認すると以下のように False を返す

ghci> check_if_it's_a_category (listOfData :: [Cat_B3'])
isCategory: False
Details: [True,True,True,True,False,True,True,True]

(ソースコードを見ればわかるように False となっている5番目の公理は「射 \(f,g\) について、\(f\) のコドメインと \(g\) のドメインが共通であるとき、それらは合成可能であり、それらの合成射 \(h\) は一意的に定まる」という公理である。)

実際にそれらの合成射を調べてみると以下のようになる

ghci> CatB3_f `comp` CatB3_g
CatB3_h
ghci> CatB3'_f `comp` CatB3'_g
*** Exception: Prelude.undefined
CallStack (from HasCallStack):
  error, called at libraries\base\GHC\Err.hs:74:14 in base:GHC.Err
  undefined, called at main.hs:41:5 in main:Main

2つの平行な矢印の成す圏

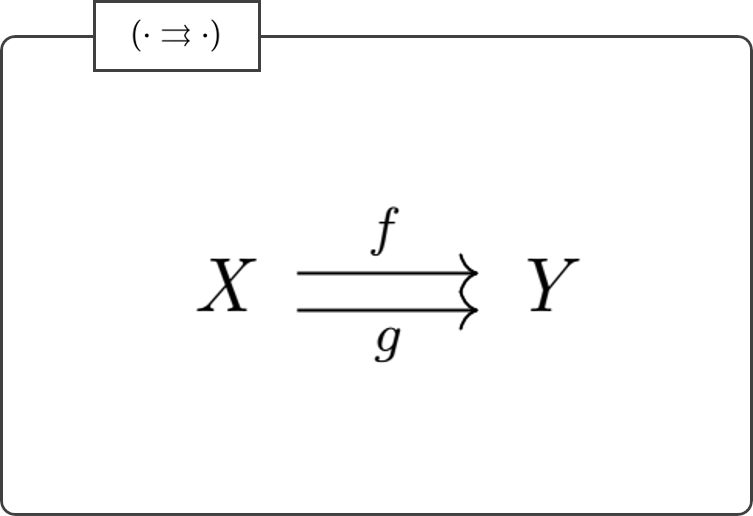
まず

\[ \begin{align} &\forall h[h=X \vee h=Y \vee h=f \vee h=g] \\ & \neg(f = g) \\ \end{align} \]

という公理を踏まえたうえで、以下のように合成の規則を与えた矢印たちは圏をなす。(ここではその圏を \((\cdot \rightrightarrows \cdot)\) とラベル付けることにする。)

\[ \begin{align} X {\sf \, ⨟ \,} X &:= X \\ Y {\sf \, ⨟ \,} Y &:= Y \\ &\\ X {\sf \, ⨟ \,} f &:= f \\ X {\sf \, ⨟ \,} g &:= g \\ &\\ f {\sf \, ⨟ \,} Y &:= f \\ g {\sf \, ⨟ \,} Y &:= g \\ \end{align} \]

余談

平行な射に対する相等関係 (平行な射全体の空間がホモトピー0型であるとすること) は理に適っていて、「それら平行な射の間に相等関係が成立しない」という公理を課すことについては問題ない。
一方で「対象同士の間に相等関係が成立しない」という言明は問題視される傾向にある。

とはいえ合成規則を愚直に定める際に \(\neg({\rm \_comp}(X,Y,X))\), \(\neg({\rm \_comp}(X,Y,Y))\), \(\neg({\rm \_comp}(X,Y,f))\), \(\neg({\rm \_comp}(X,Y,g))\) (\(X\) と \(Y\) の間で合成が定義できない) が公理として入り込むことにより、\(X\) と \(Y\) は明確に区別されることになるため「\(X\) と \(Y\) が同じ可能性が捨てきれないのでは？」という心配は無用である。

(この圏の公理化の中で対象の間の相等関係は、ドメインやコドメインの一意性を記述するために必要になるが、その辺りの問題はホモトピー型理論へ移行した際に解消される。)

スパン (span)

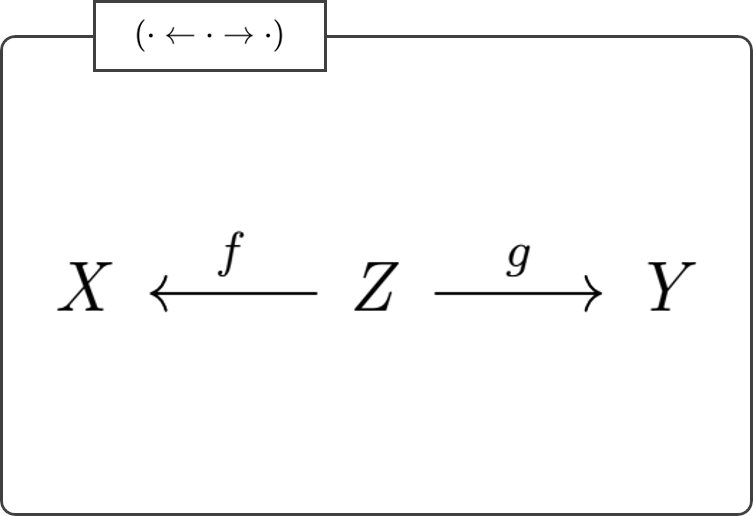
以下のように合成の規則を与えた矢印たちは圏をなし、その形の圏はしばしばスパン (span) と呼ばれる。(ここではその圏を \((\cdot \leftarrow \cdot \rightarrow \cdot)\) とラベル付けることにする。)

\[ \begin{align} X {\sf \, ⨟ \,} X &:= X \\ Y {\sf \, ⨟ \,} Y &:= Y \\ Z {\sf \, ⨟ \,} Z &:= Z \\ &\\ Z {\sf \, ⨟ \,} f &:= f \\ Z {\sf \, ⨟ \,} g &:= g \\ &\\ f {\sf \, ⨟ \,} X &:= f \\ g {\sf \, ⨟ \,} Y &:= g \\ \end{align} \]

co-スパン (co-span)

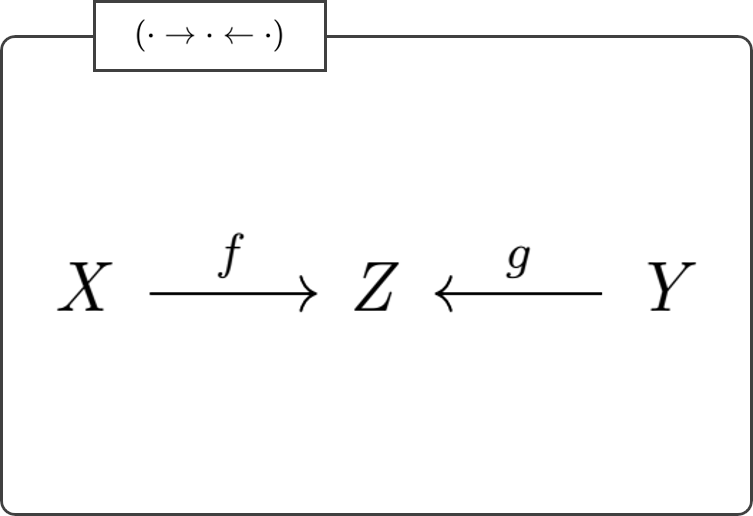
以下のように合成の規則を与えた矢印たちは圏をなす。(ここではその圏を \((\cdot \rightarrow \cdot \leftarrow \cdot)\) とラベル付けることにする。)

\[ \begin{align} X {\sf \, ⨟ \,} X &:= X \\ Y {\sf \, ⨟ \,} Y &:= Y \\ Z {\sf \, ⨟ \,} Z &:= Z \\ &\\ X {\sf \, ⨟ \,} f &:= f \\ Y {\sf \, ⨟ \,} g &:= g \\ &\\ f {\sf \, ⨟ \,} Z &:= f \\ g {\sf \, ⨟ \,} Z &:= g \\ \end{align} \]

特に深い意味のない少し複雑な謎の圏

以上のシンプルな例だけだとつまらないかもしれないので、特に重要な意味はないが少しだけ複雑な圏を一つ紹介しておく。
(これを見れば、圏の住人である射の実体は単なる矢印でしかないことをわかってもらえるだろうか)

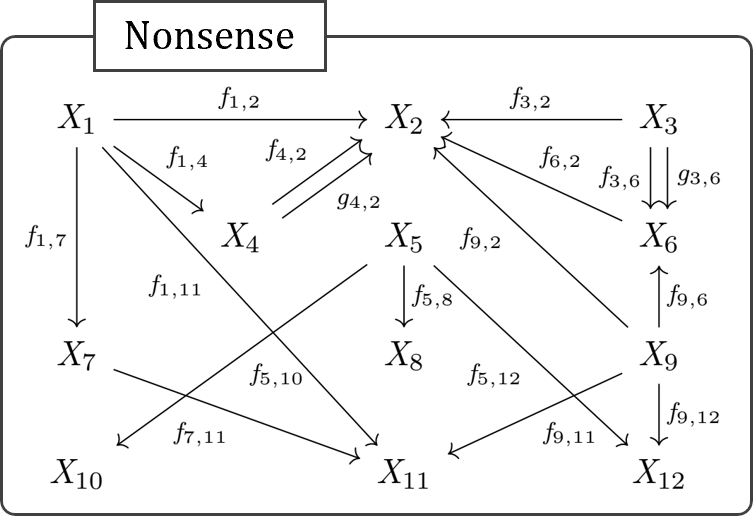
どのように矢印の合成を定義しているのかはソースコードを参照。
(ソースコードで行われている定義は「_ -> False」のおかげで一見短くみえるが、実際に一階の理論として公理を全て書き下そうとすると、その総数は 28800 個以上にもなる。)

Haskell を使ってこのデータ群が圏の公理を全て満たすかを確認すると以下のように True を返す

ghci> check_if_it's_a_category (listOfData :: [Cat_NS1])
isCategory: True
Details: [True,True,True,True,True,True,True,True]

但しデータ数が多いため、量化子が多く使用されている結合性公理の総当たりによる確認には時間がかかる。
実際、上の結果を得るために 12分42秒かかっている。

おまけ

圏の公理を満たすか否かの愚直な判定に用いた Haskell コード

import Data.Void

class Eq a => (FiniteCategory a) where
  listOfData :: [a]
  domR  :: (a,a)   -> Bool
  codR  :: (a,a)   -> Bool
  compR :: (a,a,a) -> Bool


dom :: (FiniteCategory a) => a -> a
dom f =
  if length tbl /= 1 then
    undefined
  else
    tbl !! 0
  where
    tbl = do
      x <- listOfData
      if domR(f,x) then
        return x
      else
        []

cod :: (FiniteCategory a) => a -> a
cod f =
  if length tbl /= 1 then
    undefined
  else
    tbl !! 0
  where
    tbl = do
      x <- listOfData
      if codR(f,x) then
        return x
      else
        []

comp :: (FiniteCategory a) => a -> a -> a
comp f g =
  if length tbl /= 1 then
    undefined
  else
    tbl !! 0
  where
    tbl = do
      x <- listOfData
      if compR(f,g,x) then
        return x
      else
        []

-- 空圏
type EmptyCat = Void

instance FiniteCategory EmptyCat where
  listOfData = []
  domR  _ = False
  codR  _ = False
  compR _ = False

-- 終圏
data TerminalCat = Pt deriving (Show,Eq)

instance FiniteCategory TerminalCat where
  listOfData = [Pt]
  domR  _ = True
  codR  _ = True
  compR _ = True

-- 区間圏
data IntervalCat = Intv_X | Intv_Y | Intv_f deriving (Show,Eq)

instance FiniteCategory IntervalCat where
  listOfData = [Intv_X, Intv_Y, Intv_f]
  domR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (Intv_X, Intv_X) -> True
      (Intv_f, Intv_X) -> True
      (Intv_Y, Intv_Y) -> True
      _                -> False
  codR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (Intv_X, Intv_X) -> True
      (Intv_Y, Intv_Y) -> True
      (Intv_f, Intv_Y) -> True
      _                -> False
  compR (arrow1, arrow2, arrow3) =
    case (arrow1, arrow2, arrow3) of
      (Intv_X, Intv_X, Intv_X) -> True
      (Intv_X, Intv_f, Intv_f) -> True
      (Intv_Y, Intv_Y, Intv_Y) -> True
      (Intv_f, Intv_Y, Intv_f) -> True
      _                        -> False


-- 圏 𝟛
data Cat_B3 = CatB3_X | CatB3_Y | CatB3_Z | CatB3_f | CatB3_g | CatB3_h deriving (Show,Eq)

instance FiniteCategory Cat_B3 where
  listOfData = [CatB3_X, CatB3_Y, CatB3_Z, CatB3_f, CatB3_g, CatB3_h]
  domR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatB3_X, CatB3_X) -> True
      (CatB3_Y, CatB3_Y) -> True
      (CatB3_Z, CatB3_Z) -> True
      (CatB3_f, CatB3_X) -> True
      (CatB3_g, CatB3_Y) -> True
      (CatB3_h, CatB3_X) -> True
      _                  -> False
  codR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatB3_X, CatB3_X) -> True
      (CatB3_Y, CatB3_Y) -> True
      (CatB3_Z, CatB3_Z) -> True
      (CatB3_f, CatB3_Y) -> True
      (CatB3_g, CatB3_Z) -> True
      (CatB3_h, CatB3_Z) -> True
      _                  -> False
  compR (arrow1, arrow2, arrow3) =
    case (arrow1, arrow2, arrow3) of
      (CatB3_X, CatB3_X, CatB3_X) -> True
      (CatB3_Y, CatB3_Y, CatB3_Y) -> True
      (CatB3_Z, CatB3_Z, CatB3_Z) -> True
      (CatB3_X, CatB3_f, CatB3_f) -> True
      (CatB3_f, CatB3_Y, CatB3_f) -> True
      (CatB3_Y, CatB3_g, CatB3_g) -> True
      (CatB3_g, CatB3_Z, CatB3_g) -> True
      (CatB3_X, CatB3_h, CatB3_h) -> True
      (CatB3_h, CatB3_Z, CatB3_h) -> True
      (CatB3_f, CatB3_g, CatB3_h) -> True
      _                           -> False


-- 圏 𝟛 から矢印 h を取り除いた有向グラフ
data Cat_B3' = CatB3'_X | CatB3'_Y | CatB3'_Z | CatB3'_f | CatB3'_g deriving (Show,Eq)

instance FiniteCategory Cat_B3' where
  listOfData = [CatB3'_X, CatB3'_Y, CatB3'_Z, CatB3'_f, CatB3'_g]
  domR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatB3'_X, CatB3'_X) -> True
      (CatB3'_Y, CatB3'_Y) -> True
      (CatB3'_Z, CatB3'_Z) -> True
      (CatB3'_f, CatB3'_X) -> True
      (CatB3'_g, CatB3'_Y) -> True
      _                    -> False
  codR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatB3'_X, CatB3'_X) -> True
      (CatB3'_Y, CatB3'_Y) -> True
      (CatB3'_Z, CatB3'_Z) -> True
      (CatB3'_f, CatB3'_Y) -> True
      (CatB3'_g, CatB3'_Z) -> True
      _                    -> False
  compR (arrow1, arrow2, arrow3) =
    case (arrow1, arrow2, arrow3) of
      (CatB3'_X, CatB3'_X, CatB3'_X) -> True
      (CatB3'_Y, CatB3'_Y, CatB3'_Y) -> True
      (CatB3'_Z, CatB3'_Z, CatB3'_Z) -> True
      (CatB3'_X, CatB3'_f, CatB3'_f) -> True
      (CatB3'_f, CatB3'_Y, CatB3'_f) -> True
      (CatB3'_Y, CatB3'_g, CatB3'_g) -> True
      (CatB3'_g, CatB3'_Z, CatB3'_g) -> True
      _                              -> False


-- 特に深い意味のない圏1
data Cat_NS1 = 
  CatNS1_X1 | CatNS1_X2 | CatNS1_X3 | CatNS1_X4  | CatNS1_X5  | CatNS1_X6  |
  CatNS1_X7 | CatNS1_X8 | CatNS1_X9 | CatNS1_X10 | CatNS1_X11 | CatNS1_X12 |
  CatNS1_f'1_2'  | CatNS1_f'1_4'  | CatNS1_f'1_7'  | CatNS1_f'1_11' |
  CatNS1_f'3_2'  | CatNS1_f'3_6'  | CatNS1_g'3_6'  |
  CatNS1_f'4_2'  | CatNS1_g'4_2'  |
  CatNS1_f'5_8'  | CatNS1_f'5_10' | CatNS1_f'5_12' |
  CatNS1_f'6_2'  |
  CatNS1_f'7_11' |
  CatNS1_f'9_2'  | CatNS1_f'9_6'  | CatNS1_f'9_11' | CatNS1_f'9_12'
    deriving (Show,Eq)

instance FiniteCategory Cat_NS1 where
  listOfData =
    [ CatNS1_X1 , CatNS1_X2 , CatNS1_X3 , CatNS1_X4  , CatNS1_X5  , CatNS1_X6 
    , CatNS1_X7 , CatNS1_X8 , CatNS1_X9 , CatNS1_X10 , CatNS1_X11 , CatNS1_X12
    , CatNS1_f'1_2'  , CatNS1_f'1_4'  , CatNS1_f'1_7'  , CatNS1_f'1_11'
    , CatNS1_f'3_2'  , CatNS1_f'3_6'  , CatNS1_g'3_6'
    , CatNS1_f'4_2'  , CatNS1_g'4_2'
    , CatNS1_f'5_8'  , CatNS1_f'5_10' , CatNS1_f'5_12'
    , CatNS1_f'6_2'
    , CatNS1_f'7_11'
    , CatNS1_f'9_2'  , CatNS1_f'9_6'  , CatNS1_f'9_11' , CatNS1_f'9_12' ]

  domR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatNS1_X1,  CatNS1_X1) -> True
      (CatNS1_X2,  CatNS1_X2) -> True
      (CatNS1_X3,  CatNS1_X3) -> True
      (CatNS1_X4,  CatNS1_X4) -> True
      (CatNS1_X5,  CatNS1_X5) -> True
      (CatNS1_X6,  CatNS1_X6) -> True
      (CatNS1_X7,  CatNS1_X7) -> True
      (CatNS1_X8,  CatNS1_X8) -> True
      (CatNS1_X9,  CatNS1_X9) -> True
      (CatNS1_X10, CatNS1_X10) -> True
      (CatNS1_X11, CatNS1_X11) -> True
      (CatNS1_X12, CatNS1_X12) -> True

      (CatNS1_f'1_2',  CatNS1_X1) -> True
      (CatNS1_f'1_4',  CatNS1_X1) -> True
      (CatNS1_f'1_7',  CatNS1_X1) -> True
      (CatNS1_f'1_11', CatNS1_X1) -> True
      (CatNS1_f'3_2',  CatNS1_X3) -> True
      (CatNS1_f'3_6',  CatNS1_X3) -> True
      (CatNS1_g'3_6',  CatNS1_X3) -> True
      (CatNS1_f'4_2',  CatNS1_X4) -> True
      (CatNS1_g'4_2',  CatNS1_X4) -> True
      (CatNS1_f'5_8',  CatNS1_X5) -> True
      (CatNS1_f'5_10', CatNS1_X5) -> True
      (CatNS1_f'5_12', CatNS1_X5) -> True
      (CatNS1_f'6_2',  CatNS1_X6) -> True
      (CatNS1_f'7_11', CatNS1_X7) -> True
      (CatNS1_f'9_2',  CatNS1_X9) -> True
      (CatNS1_f'9_6',  CatNS1_X9) -> True
      (CatNS1_f'9_11', CatNS1_X9) -> True
      (CatNS1_f'9_12', CatNS1_X9) -> True

      _ -> False

  codR (arrow1, arrow2) =
    case (arrow1, arrow2) of
      (CatNS1_X1,  CatNS1_X1)  -> True
      (CatNS1_X2,  CatNS1_X2)  -> True
      (CatNS1_X3,  CatNS1_X3)  -> True
      (CatNS1_X4,  CatNS1_X4)  -> True
      (CatNS1_X5,  CatNS1_X5)  -> True
      (CatNS1_X6,  CatNS1_X6)  -> True
      (CatNS1_X7,  CatNS1_X7)  -> True
      (CatNS1_X8,  CatNS1_X8)  -> True
      (CatNS1_X9,  CatNS1_X9)  -> True
      (CatNS1_X10, CatNS1_X10) -> True
      (CatNS1_X11, CatNS1_X11) -> True
      (CatNS1_X12, CatNS1_X12) -> True

      (CatNS1_f'1_2',  CatNS1_X2)  -> True
      (CatNS1_f'1_4',  CatNS1_X4)  -> True
      (CatNS1_f'1_7',  CatNS1_X7)  -> True
      (CatNS1_f'1_11', CatNS1_X11) -> True
      (CatNS1_f'3_2',  CatNS1_X2)  -> True
      (CatNS1_f'3_6',  CatNS1_X6)  -> True
      (CatNS1_g'3_6',  CatNS1_X6)  -> True
      (CatNS1_f'4_2',  CatNS1_X2)  -> True
      (CatNS1_g'4_2',  CatNS1_X2)  -> True
      (CatNS1_f'5_8',  CatNS1_X8)  -> True
      (CatNS1_f'5_10', CatNS1_X10) -> True
      (CatNS1_f'5_12', CatNS1_X12) -> True
      (CatNS1_f'6_2',  CatNS1_X2)  -> True
      (CatNS1_f'7_11', CatNS1_X11) -> True
      (CatNS1_f'9_2',  CatNS1_X2)  -> True
      (CatNS1_f'9_6',  CatNS1_X6)  -> True
      (CatNS1_f'9_11', CatNS1_X11) -> True
      (CatNS1_f'9_12', CatNS1_X12) -> True

      _ -> False

  compR (arrow1, arrow2, arrow3) =
    case (arrow1, arrow2, arrow3) of
      (CatNS1_X1,  CatNS1_X1,  CatNS1_X1)  -> True
      (CatNS1_X2,  CatNS1_X2,  CatNS1_X2)  -> True
      (CatNS1_X3,  CatNS1_X3,  CatNS1_X3)  -> True
      (CatNS1_X4,  CatNS1_X4,  CatNS1_X4)  -> True
      (CatNS1_X5,  CatNS1_X5,  CatNS1_X5)  -> True
      (CatNS1_X6,  CatNS1_X6,  CatNS1_X6)  -> True
      (CatNS1_X7,  CatNS1_X7,  CatNS1_X7)  -> True
      (CatNS1_X8,  CatNS1_X8,  CatNS1_X8)  -> True
      (CatNS1_X9,  CatNS1_X9,  CatNS1_X9)  -> True
      (CatNS1_X10, CatNS1_X10, CatNS1_X10) -> True
      (CatNS1_X11, CatNS1_X11, CatNS1_X11) -> True
      (CatNS1_X12, CatNS1_X12, CatNS1_X12) -> True

      (CatNS1_X1, CatNS1_f'1_2',  CatNS1_f'1_2')  -> True
      (CatNS1_X1, CatNS1_f'1_4',  CatNS1_f'1_4')  -> True
      (CatNS1_X1, CatNS1_f'1_7',  CatNS1_f'1_7')  -> True
      (CatNS1_X1, CatNS1_f'1_11', CatNS1_f'1_11') -> True
      (CatNS1_X3, CatNS1_f'3_2',  CatNS1_f'3_2')  -> True
      (CatNS1_X3, CatNS1_f'3_6',  CatNS1_f'3_6')  -> True
      (CatNS1_X3, CatNS1_g'3_6',  CatNS1_g'3_6')  -> True
      (CatNS1_X4, CatNS1_f'4_2',  CatNS1_f'4_2')  -> True
      (CatNS1_X4, CatNS1_g'4_2',  CatNS1_g'4_2')  -> True
      (CatNS1_X5, CatNS1_f'5_8',  CatNS1_f'5_8')  -> True
      (CatNS1_X5, CatNS1_f'5_10', CatNS1_f'5_10') -> True
      (CatNS1_X5, CatNS1_f'5_12', CatNS1_f'5_12') -> True
      (CatNS1_X6, CatNS1_f'6_2',  CatNS1_f'6_2')  -> True
      (CatNS1_X7, CatNS1_f'7_11', CatNS1_f'7_11') -> True
      (CatNS1_X9, CatNS1_f'9_2',  CatNS1_f'9_2')  -> True
      (CatNS1_X9, CatNS1_f'9_6',  CatNS1_f'9_6')  -> True
      (CatNS1_X9, CatNS1_f'9_11', CatNS1_f'9_11') -> True
      (CatNS1_X9, CatNS1_f'9_12', CatNS1_f'9_12') -> True

      (CatNS1_f'1_2',  CatNS1_X2,  CatNS1_f'1_2')  -> True
      (CatNS1_f'1_4',  CatNS1_X4,  CatNS1_f'1_4')  -> True
      (CatNS1_f'1_7',  CatNS1_X7,  CatNS1_f'1_7')  -> True
      (CatNS1_f'1_11', CatNS1_X11, CatNS1_f'1_11') -> True
      (CatNS1_f'3_2',  CatNS1_X2,  CatNS1_f'3_2')  -> True
      (CatNS1_f'3_6',  CatNS1_X6,  CatNS1_f'3_6')  -> True
      (CatNS1_g'3_6',  CatNS1_X6,  CatNS1_g'3_6')  -> True
      (CatNS1_f'4_2',  CatNS1_X2,  CatNS1_f'4_2')  -> True
      (CatNS1_g'4_2',  CatNS1_X2,  CatNS1_g'4_2')  -> True
      (CatNS1_f'5_8',  CatNS1_X8,  CatNS1_f'5_8')  -> True
      (CatNS1_f'5_10', CatNS1_X10, CatNS1_f'5_10') -> True
      (CatNS1_f'5_12', CatNS1_X12, CatNS1_f'5_12') -> True
      (CatNS1_f'6_2',  CatNS1_X2,  CatNS1_f'6_2')  -> True
      (CatNS1_f'7_11', CatNS1_X11, CatNS1_f'7_11') -> True
      (CatNS1_f'9_2',  CatNS1_X2,  CatNS1_f'9_2')  -> True
      (CatNS1_f'9_6',  CatNS1_X6,  CatNS1_f'9_6')  -> True
      (CatNS1_f'9_11', CatNS1_X11, CatNS1_f'9_11') -> True
      (CatNS1_f'9_12', CatNS1_X12, CatNS1_f'9_12') -> True

      (CatNS1_f'1_4', CatNS1_f'4_2',  CatNS1_f'1_2')  -> True
      (CatNS1_f'1_4', CatNS1_g'4_2',  CatNS1_f'1_2')  -> True
      (CatNS1_f'1_7', CatNS1_f'7_11', CatNS1_f'1_11') -> True

      (CatNS1_f'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True
      (CatNS1_g'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True

      (CatNS1_f'9_6', CatNS1_f'6_2', CatNS1_f'9_2') -> True

      _ -> False


check_if_it's_a_category :: (FiniteCategory a) => [a] -> IO ()
check_if_it's_a_category listOfData' =
  let
    results =
      [ _forall'(\f -> _exists'(\h -> domR(f,h) && _forall'(\i -> domR(f,i) `implies` (h == i))))
      , _forall'(\f -> _exists'(\h -> codR(f,h) && _forall'(\i -> codR(f,i) `implies` (h == i))))
      , _forall'(\f -> _forall'(\h -> domR(f,h) `implies` (domR(h,h) && codR(h,h))))
      , _forall'(\f -> _forall'(\h -> codR(f,h) `implies` (domR(h,h) && codR(h,h))))
      , _forall'(\f -> _forall'(\g -> (_exists'(\i -> codR(f,i) && domR(g,i)) `implies` _exists'(\h -> (compR(f,g,h) && _forall'(\j -> compR(f,g,j) `implies` (j == h)) )) ) ))
      , _forall'(\f -> _forall'(\g -> _forall'(\h -> compR(f,g,h) `implies` (_exists'(\i -> codR(f,i) && domR(g,i)) && (_exists'(\i -> domR(h,i) && domR(f,i)) &&_exists'(\i -> codR(h,i) && codR(g,i)))) )))
      , _forall'(\f -> _forall'(\h -> (domR(f,h) `implies` compR(h,f,f))) && _forall'(\h -> (codR(f,h) `implies` compR(f,h,f))) )
      , _forall'(\f -> _forall'(\g -> _forall'(\h -> _forall'(\j -> _forall'(\k -> _forall'(\m -> ((compR(f,g,j) && compR(g,h,k)) `implies` (compR(j,h,m) <=> compR(f,k,m))) )))))) ]    
  in
    putStr $ "isCategory: " ++ (show $ and(results)) ++ "\nDetails: " ++ (show results) ++ "\n"
  where
    _forall' p = _forall(listOfData', p)
    _exists' p = _exists(listOfData', p)


_forall :: ([a], (a -> Bool)) -> Bool
_forall (dat,_P) = and (fmap _P $ dat)

_exists :: ([a], (a -> Bool)) -> Bool
_exists (dat,_P) = or  (fmap _P $ dat)

(<=>) x y =
  x == y

implies x y =
  x == (x && y)

Show ALL

タグ: 数学圏論 Haskell

タグ一覧:

物理学 (18)
古典力学 (9)
量子力学 (5)
数学 (56)
圏論 (32)
位相 (1)
線形代数 (7)
高校数学 (4)
プログラミング (28)
C言語 (4)
Haskell (32)
Java (1)
Python (2)
PureScript (3)
日記 (40)
小ネタ (17)
音楽 (4)
ピアノ (12)
ゲーム (18)
YouTube (36)

ページの先頭へ

TakuLabo

圏を一階述語論理で公理化する