雑記帳
エピック (epic) とモニック (monic)

エピック (epic)
定義
ある射 \(f:X\rightarrow Y\) が圏 \(\mathscr{C}\) で エピック (epic) であるとは、圏 \(\mathscr{C}\) 内の任意の平行な射 \(h,k:Y\rightarrow \Lambda\) に対して
\[
f {\sf \, ⨟ \,} h = f {\sf \, ⨟ \,} k \Rightarrow h = k
\]
が成り立つことをいう。
現段階では一階述語論理の上で公理的に圏を取り扱っているので、それに準拠したフォーマルな書き方をすると
\[
{\rm isEpic}(f) :\Leftrightarrow \forall h \forall k [\exists l[{\rm \_comp}(f,h,l)\wedge {\rm \_comp}(f,k,l)] \Rightarrow h = k]
\]
が真であるとき、\(f\) が圏 \(\mathscr{C}\) でエピックであるという。
またエピック射 (epic arrow) は、エピ (epi) または エピ射 (epimorphism) とも呼ばれる。
説明
定義をそのまま言葉にするならば、\(f:X\rightarrow Y\) がエピックであるとは
- 「\(Y\) から伸びる矢印」と「その矢印に \(f\) を前方から連結して得られる \(X\) から伸びる矢印」との間に1対1の対応が考えられる
という条件を満たしているということである。
注意してほしいのは、圏論初学者はしばしばエピック射を「全射 (surjection) / 上への写像 (onto mapping)」のようなものと捉える傾向があるように思えるが、そのイメージでエピックという概念を捉えるのはあまり適切とは言えない。
確かに、エピックは全射の概念の「簡約性質 (cancellation property)」という点に注目した一つの圏論的な抽象化であると思われるが、その抽象化を経た先にも、大本の全射が持っていた具体的なイメージが崩壊しないまま原型を留めて残っているということを期待するべきではない。
幸運にも、次に説明するモニックの場合であれば、抽象化の前の「単射」のイメージが抽象化後の「モニック射」の中でもある程度生きているが、残念ながらこのエピックの場合は、あまり原型を留めない。
余談
圏論が面白いのは、このように「エピック」という概念は、原型をあまり留めさせない程の高度な抽象化を経た先に得られるものである一方、「エピック」という概念を考える圏が特定の性質を満たしている場合、その「エピック」という概念が「全射」の概念と合致する。
つまり、「抽象化して得た概念」であったはずの「エピック」が、特定の状況下にある時、抽象化前の「全射」そのものに化けるということである。
抽象化というプロセスは、「不可逆」(抽象化の際に切り落とした情報は完全に見失うことになる) という印象を持つ人も少なくないと思うが、圏論的に抽象化された数学概念というのは、このように非常に奇妙なまでに上手く情報の復元がされるケースが多々ある。(他の例としては、「トポスの公理から全ての有限余積の存在が示せること」や「ETCS の公理から、真理値対象の濃度が2であることを示せること」などなど。)
具体例
任意の恒等射はエピック
\(f\) を恒等射 \({\rm id}_X:X\rightarrow X\) とし、任意の射 \(h,k:X\rightarrow \Lambda\) について次の関係式
\[
{\rm id}_X {\sf \, ⨟ \,} h = {\rm id}_X {\sf \, ⨟ \,} k
\]
が成り立っている状況を考える。
恒等射 \({\rm id}_X:X\rightarrow X\) の定義より、
\[
\begin{align}
{\rm id}_X {\sf \, ⨟ \,} h &= {\rm id}_X {\sf \, ⨟ \,} k \\
X {\sf \, ⨟ \,} h &= X {\sf \, ⨟ \,} k \\
h &= k \\
\end{align}
\]
よって \({\rm id}_X\) はエピック。
区間圏の持つ非自明な射はエピック
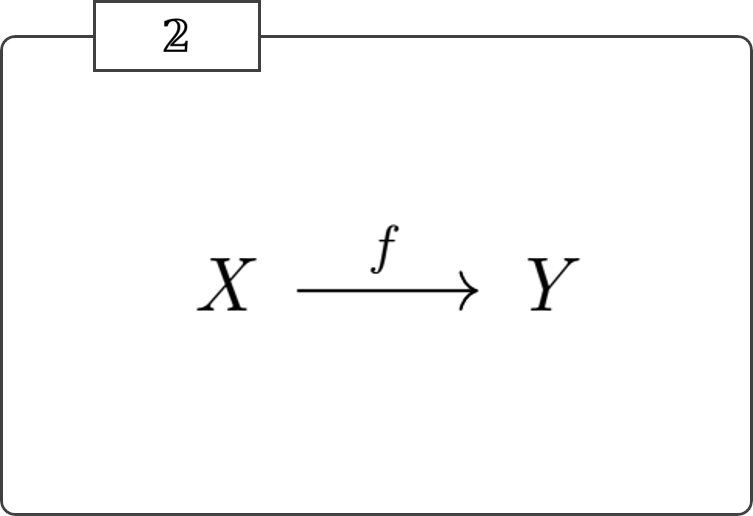
\(X,Y\) を区間圏内の2点、\(f\) を区間圏の持つ非自明な射 \(f:X\rightarrow Y\) する。
区間圏は有限グラフからなる圏 (圏の全体像となる図式が具体的に書き下せる圏) であるため、定義として与えられている論理式の真偽を愚直に総当たりすることによってエピックであるかを確かめることができる。
この作業は手作業でも可能ではあるが、煩雑であるため Haskell で論理式の真偽を愚直に調べる関数を作ってコンピュータに調べてもらう。
この作業は手作業でも可能ではあるが、煩雑であるため Haskell で論理式の真偽を愚直に調べる関数を作ってコンピュータに調べてもらう。
使用したコードはこのページのおまけセクションに載せておくが、実際に実行してみると、射 \(f:X\rightarrow Y\) がエピックであるかの判定結果として「True」が出力される。
ghci> isEpic(Arr_f)
Trueよって、\(f:X\rightarrow Y\) はエピック。
ちなみに先ほど恒等射はエピックであることを一般的に示したので当たり前ではあるが、愚直に調べてみても同様にエピックであることがわかる。
ghci> isEpic(Obj_X)
True
ghci> isEpic(Obj_Y)
Trueエピックでない射の例
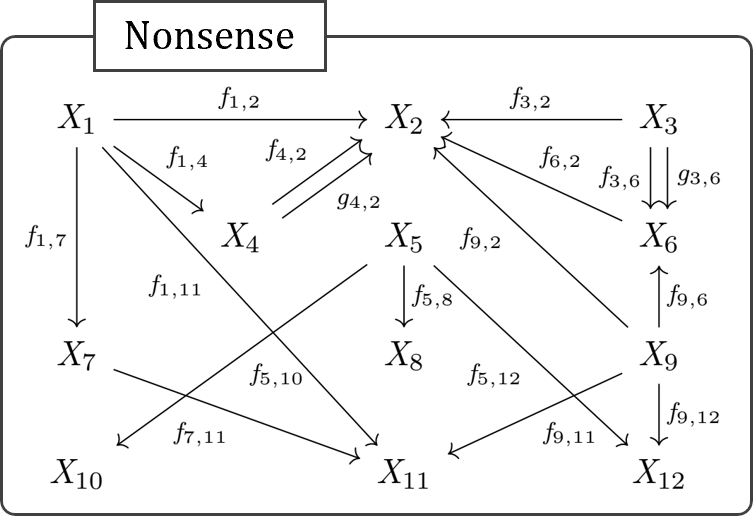
上に示した圏の持つ射 \(f_{1,4}:X_1\rightarrow X_4\) はエピックでない。
この圏も有限グラフからなるため、Brute-force method で射がエピックか否かを確かめられる。ということで先ほどと同様コンピュータに調べてもらうと以下のような結果が得られる。
ghci> isEpic(CatNS1_f'1_4')
Falseよって、\(f_{1,4}:X_1\rightarrow X_4\) はエピックでない。
因みに以下の通り、それ以外の射は漏れなく全てエピックである。
ghci> putStr $ do {x <- listOfData::[Cat_NS1]; show x ++ ":\t" ++ (show $ isEpic(x)) ++ "\n";}
CatNS1_X1: True
CatNS1_X2: True
CatNS1_X3: True
CatNS1_X4: True
CatNS1_X5: True
CatNS1_X6: True
CatNS1_X7: True
CatNS1_X8: True
CatNS1_X9: True
CatNS1_X10: True
CatNS1_X11: True
CatNS1_X12: True
CatNS1_f'1_2': True
CatNS1_f'1_4': False
CatNS1_f'1_7': True
CatNS1_f'1_11': True
CatNS1_f'3_2': True
CatNS1_f'3_6': True
CatNS1_g'3_6': True
CatNS1_f'4_2': True
CatNS1_g'4_2': True
CatNS1_f'5_8': True
CatNS1_f'5_10': True
CatNS1_f'5_12': True
CatNS1_f'6_2': True
CatNS1_f'7_11': True
CatNS1_f'9_2': True
CatNS1_f'9_6': True
CatNS1_f'9_11': True
CatNS1_f'9_12': Trueモニック (monic)
定義
ある射 \(f:X\rightarrow Y\) が圏 \(\mathscr{C}\) で モニック (monic) であるとは、圏 \(\mathscr{C}\) 内の任意の平行な射 \(h,k:L \rightarrow X\) に対して
\[
h {\sf \, ⨟ \,} f = k {\sf \, ⨟ \,} f \Rightarrow h = k
\]
が成り立つことをいう。
現段階では一階述語論理の上で公理的に圏を取り扱っているので、それに準拠したフォーマルな書き方をすると
\[
{\rm isMonic}(f) :\Leftrightarrow \forall h \forall k [\exists l[{\rm \_comp}(h,f,l)\wedge {\rm \_comp}(k,f,l)] \Rightarrow h = k]
\]
が真であるとき、\(f\) が圏 \(\mathscr{C}\) でモニックであるという。
またモニック射 (monic arrow) は、モノ (mono) または モノ射 (monomorphism) とも呼ばれる。
説明
定義をそのまま言葉にするならば、\(f:X\rightarrow Y\) がモニックであるとは
- 「\(X\) へと伸びる矢印」と「その矢印に \(f\) を後方から連結して得られる \(Y\) へと伸びる矢印」との間に1対1の対応が考えられる
という条件を満たしているということである。
これだけではエピック射で行った説明と殆ど変わらないが、この説明の中に登場する「\(X\) へと伸びる矢印」というのは「\(X\) の一般化要素」として見ることができる。
つまり上の説明は
- \(X\) の一般化要素と、モニック射 \(f\) でその一般化要素を変換して得られる \(Y\) の一般化要素との間に1対1の対応がある。
或いは
- モニック射によって出力される一般化要素が同じであれば、入力されている一般化要素が同じである
ということである。
一般的抽象的ナンセンス
モニック射同士の合成射はモニック
(周囲圏を任意の圏 \(\mathscr{C}\) とする。)
\(f:X\rightarrow Y, g:Y\rightarrow Z\) をモニック射とする。
まず、任意の射 \(h,k:L\rightarrow X\) について次の関係式
\[
h {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g) = k {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g)
\]
が成り立っている状況を考えると、
この時、射の結合性公理から
\[
\begin{align}
h {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g) &= k {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g) \\
(h {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g &= (k {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g \\
\end{align}
\]
\(g\) はモニックより
\[
((h {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g = (k {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g) \Rightarrow (h {\sf \, ⨟ \,} f) = (k {\sf \, ⨟ \,} f)
\]
が成り立つため
\[
\begin{align}
(h {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g &= (k {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} g \\
h {\sf \, ⨟ \,} f &= k {\sf \, ⨟ \,} f \\
\end{align}
\]
\(f\) も同様にモニックより
\[
h {\sf \, ⨟ \,} f = k {\sf \, ⨟ \,} f \Rightarrow h = k
\]
が成り立つ
つまり
\[
h {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g) = k {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} g) \Rightarrow h = k
\]
が任意の \(h,k\) について成立するため \(f {\sf \, ⨟ \,} g\) はモニック。
具体例
任意の恒等射はモニック
\(f\) を恒等射 \({\rm id}_X:X\rightarrow X\) とし、任意の射 \(h,k:L\rightarrow X\) について次の関係式
\[
h {\sf \, ⨟ \,} {\rm id}_X = k {\sf \, ⨟ \,} {\rm id}_X
\]
が成り立っている状況を考える。
恒等射 \({\rm id}_X:X\rightarrow X\) の定義より、
\[
\begin{align}
h {\sf \, ⨟ \,} {\rm id}_X &= k {\sf \, ⨟ \,} {\rm id}_X \\
h {\sf \, ⨟ \,} X &= k {\sf \, ⨟ \,} X \\
h &= k \\
\end{align}
\]
よって \({\rm id}_X\) はモニック。
区間圏の持つ非自明な射はモニック
\(X,Y\) を区間圏内の2点、\(f\) を区間圏の持つ非自明な射 \(f:X\rightarrow Y\) する。
エピックの節で行ったのと全く同様にして、コンピュータによってモニックか否かを愚直に判定する。
ghci> isMonic(Arr_f)
Trueよって、\(f:X\rightarrow Y\) はモニック。
双対性
これら2つの圏論的な概念が圏論的双対で結ばれている
つまり以下のようなマクロ置換を考える
- \({\rm \_comp}(f,g,h)\) を \({\rm \_comp}(g,f,h)\)
- \({\rm \_dom}(f,h)\) を \({\rm \_cod}(f,h)\)
- \({\rm \_cod}(f,h)\) を \({\rm \_dom}(f,h)\)
実際にやってみると、エピックの定義
\[
\forall h \forall k [\exists l[{\rm \_comp}(f,h,l)\wedge {\rm \_comp}(f,k,l)] \Rightarrow h = k]
\]
からは
\[
\forall h \forall k [\exists l[{\rm \_comp}(h,f,l)\wedge {\rm \_comp}(k,f,l)] \Rightarrow h = k]
\]
というようにモニックの定義が得られ、逆にモニックの定義からはエピックの定義が得られる。
おまけ
エピック・モニックの愚直な判定に用いた Haskell コード
class Eq a => (FiniteCategory a) where
listOfData :: [a]
domR :: (a,a) -> Bool
codR :: (a,a) -> Bool
compR :: (a,a,a) -> Bool
-- 区間圏
data IntervalCat = Obj_X | Obj_Y | Arr_f deriving Eq
instance FiniteCategory IntervalCat where
listOfData = [Obj_X, Obj_Y, Arr_f]
domR (arrow1, arrow2) =
case (arrow1, arrow2) of
(Obj_X, Obj_X) -> True
(Arr_f, Obj_X) -> True
(Obj_Y, Obj_Y) -> True
_ -> False
codR (arrow1, arrow2) =
case (arrow1, arrow2) of
(Obj_X, Obj_X) -> True
(Obj_Y, Obj_Y) -> True
(Arr_f, Obj_Y) -> True
_ -> False
compR (arrow1, arrow2, arrow3) =
case (arrow1, arrow2, arrow3) of
(Obj_X, Obj_X, Obj_X) -> True
(Obj_X, Arr_f, Arr_f) -> True
(Obj_Y, Obj_Y, Obj_Y) -> True
(Arr_f, Obj_Y, Arr_f) -> True
_ -> False
-- 特に深い意味のない圏1
data Cat_NS1 =
CatNS1_X1 | CatNS1_X2 | CatNS1_X3 | CatNS1_X4 | CatNS1_X5 | CatNS1_X6 |
CatNS1_X7 | CatNS1_X8 | CatNS1_X9 | CatNS1_X10 | CatNS1_X11 | CatNS1_X12 |
CatNS1_f'1_2' | CatNS1_f'1_4' | CatNS1_f'1_7' | CatNS1_f'1_11' |
CatNS1_f'3_2' | CatNS1_f'3_6' | CatNS1_g'3_6' |
CatNS1_f'4_2' | CatNS1_g'4_2' |
CatNS1_f'5_8' | CatNS1_f'5_10' | CatNS1_f'5_12' |
CatNS1_f'6_2' |
CatNS1_f'7_11' |
CatNS1_f'9_2' | CatNS1_f'9_6' | CatNS1_f'9_11' | CatNS1_f'9_12'
deriving (Show,Eq)
instance FiniteCategory Cat_NS1 where
listOfData =
[ CatNS1_X1 , CatNS1_X2 , CatNS1_X3 , CatNS1_X4 , CatNS1_X5 , CatNS1_X6
, CatNS1_X7 , CatNS1_X8 , CatNS1_X9 , CatNS1_X10 , CatNS1_X11 , CatNS1_X12
, CatNS1_f'1_2' , CatNS1_f'1_4' , CatNS1_f'1_7' , CatNS1_f'1_11'
, CatNS1_f'3_2' , CatNS1_f'3_6' , CatNS1_g'3_6'
, CatNS1_f'4_2' , CatNS1_g'4_2'
, CatNS1_f'5_8' , CatNS1_f'5_10' , CatNS1_f'5_12'
, CatNS1_f'6_2'
, CatNS1_f'7_11'
, CatNS1_f'9_2' , CatNS1_f'9_6' , CatNS1_f'9_11' , CatNS1_f'9_12' ]
domR (arrow1, arrow2) =
case (arrow1, arrow2) of
(CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12) -> True
(CatNS1_f'1_2', CatNS1_X1) -> True
(CatNS1_f'1_4', CatNS1_X1) -> True
(CatNS1_f'1_7', CatNS1_X1) -> True
(CatNS1_f'1_11', CatNS1_X1) -> True
(CatNS1_f'3_2', CatNS1_X3) -> True
(CatNS1_f'3_6', CatNS1_X3) -> True
(CatNS1_g'3_6', CatNS1_X3) -> True
(CatNS1_f'4_2', CatNS1_X4) -> True
(CatNS1_g'4_2', CatNS1_X4) -> True
(CatNS1_f'5_8', CatNS1_X5) -> True
(CatNS1_f'5_10', CatNS1_X5) -> True
(CatNS1_f'5_12', CatNS1_X5) -> True
(CatNS1_f'6_2', CatNS1_X6) -> True
(CatNS1_f'7_11', CatNS1_X7) -> True
(CatNS1_f'9_2', CatNS1_X9) -> True
(CatNS1_f'9_6', CatNS1_X9) -> True
(CatNS1_f'9_11', CatNS1_X9) -> True
(CatNS1_f'9_12', CatNS1_X9) -> True
_ -> False
codR (arrow1, arrow2) =
case (arrow1, arrow2) of
(CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12) -> True
(CatNS1_f'1_2', CatNS1_X2) -> True
(CatNS1_f'1_4', CatNS1_X4) -> True
(CatNS1_f'1_7', CatNS1_X7) -> True
(CatNS1_f'1_11', CatNS1_X11) -> True
(CatNS1_f'3_2', CatNS1_X2) -> True
(CatNS1_f'3_6', CatNS1_X6) -> True
(CatNS1_g'3_6', CatNS1_X6) -> True
(CatNS1_f'4_2', CatNS1_X2) -> True
(CatNS1_g'4_2', CatNS1_X2) -> True
(CatNS1_f'5_8', CatNS1_X8) -> True
(CatNS1_f'5_10', CatNS1_X10) -> True
(CatNS1_f'5_12', CatNS1_X12) -> True
(CatNS1_f'6_2', CatNS1_X2) -> True
(CatNS1_f'7_11', CatNS1_X11) -> True
(CatNS1_f'9_2', CatNS1_X2) -> True
(CatNS1_f'9_6', CatNS1_X6) -> True
(CatNS1_f'9_11', CatNS1_X11) -> True
(CatNS1_f'9_12', CatNS1_X12) -> True
_ -> False
compR (arrow1, arrow2, arrow3) =
case (arrow1, arrow2, arrow3) of
(CatNS1_X1, CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12, CatNS1_X12) -> True
(CatNS1_X1, CatNS1_f'1_2', CatNS1_f'1_2') -> True
(CatNS1_X1, CatNS1_f'1_4', CatNS1_f'1_4') -> True
(CatNS1_X1, CatNS1_f'1_7', CatNS1_f'1_7') -> True
(CatNS1_X1, CatNS1_f'1_11', CatNS1_f'1_11') -> True
(CatNS1_X3, CatNS1_f'3_2', CatNS1_f'3_2') -> True
(CatNS1_X3, CatNS1_f'3_6', CatNS1_f'3_6') -> True
(CatNS1_X3, CatNS1_g'3_6', CatNS1_g'3_6') -> True
(CatNS1_X4, CatNS1_f'4_2', CatNS1_f'4_2') -> True
(CatNS1_X4, CatNS1_g'4_2', CatNS1_g'4_2') -> True
(CatNS1_X5, CatNS1_f'5_8', CatNS1_f'5_8') -> True
(CatNS1_X5, CatNS1_f'5_10', CatNS1_f'5_10') -> True
(CatNS1_X5, CatNS1_f'5_12', CatNS1_f'5_12') -> True
(CatNS1_X6, CatNS1_f'6_2', CatNS1_f'6_2') -> True
(CatNS1_X7, CatNS1_f'7_11', CatNS1_f'7_11') -> True
(CatNS1_X9, CatNS1_f'9_2', CatNS1_f'9_2') -> True
(CatNS1_X9, CatNS1_f'9_6', CatNS1_f'9_6') -> True
(CatNS1_X9, CatNS1_f'9_11', CatNS1_f'9_11') -> True
(CatNS1_X9, CatNS1_f'9_12', CatNS1_f'9_12') -> True
(CatNS1_f'1_2', CatNS1_X2, CatNS1_f'1_2') -> True
(CatNS1_f'1_4', CatNS1_X4, CatNS1_f'1_4') -> True
(CatNS1_f'1_7', CatNS1_X7, CatNS1_f'1_7') -> True
(CatNS1_f'1_11', CatNS1_X11, CatNS1_f'1_11') -> True
(CatNS1_f'3_2', CatNS1_X2, CatNS1_f'3_2') -> True
(CatNS1_f'3_6', CatNS1_X6, CatNS1_f'3_6') -> True
(CatNS1_g'3_6', CatNS1_X6, CatNS1_g'3_6') -> True
(CatNS1_f'4_2', CatNS1_X2, CatNS1_f'4_2') -> True
(CatNS1_g'4_2', CatNS1_X2, CatNS1_g'4_2') -> True
(CatNS1_f'5_8', CatNS1_X8, CatNS1_f'5_8') -> True
(CatNS1_f'5_10', CatNS1_X10, CatNS1_f'5_10') -> True
(CatNS1_f'5_12', CatNS1_X12, CatNS1_f'5_12') -> True
(CatNS1_f'6_2', CatNS1_X2, CatNS1_f'6_2') -> True
(CatNS1_f'7_11', CatNS1_X11, CatNS1_f'7_11') -> True
(CatNS1_f'9_2', CatNS1_X2, CatNS1_f'9_2') -> True
(CatNS1_f'9_6', CatNS1_X6, CatNS1_f'9_6') -> True
(CatNS1_f'9_11', CatNS1_X11, CatNS1_f'9_11') -> True
(CatNS1_f'9_12', CatNS1_X12, CatNS1_f'9_12') -> True
(CatNS1_f'1_4', CatNS1_f'4_2', CatNS1_f'1_2') -> True
(CatNS1_f'1_4', CatNS1_g'4_2', CatNS1_f'1_2') -> True
(CatNS1_f'1_7', CatNS1_f'7_11', CatNS1_f'1_11') -> True
(CatNS1_f'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True
(CatNS1_g'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True
(CatNS1_f'9_6', CatNS1_f'6_2', CatNS1_f'9_2') -> True
_ -> False
-- エピックか否かの判定式
isEpic :: (FiniteCategory a) => a -> Bool
isEpic f =
_forall'(\h -> _forall'(\k -> _exists'(\l -> compR(f,h,l) && compR(f,k,l)) `implies` (h == k)))
where
_forall' p = _forall(listOfData, p)
_exists' p = _exists(listOfData, p)
-- モニックか否かの判定式
isMonic :: (FiniteCategory a) => a -> Bool
isMonic f =
_forall'(\h -> _forall'(\k -> _exists'(\l -> compR(h,f,l) && compR(k,f,l)) `implies` (h == k)))
where
_forall' p = _forall(listOfData, p)
_exists' p = _exists(listOfData, p)
_forall :: ([a], (a -> Bool)) -> Bool
_forall (dat,_P) = and (fmap _P $ dat)
_exists :: ([a], (a -> Bool)) -> Bool
_exists (dat,_P) = or (fmap _P $ dat)
implies x y = (not x) || yタグ一覧:
