雑記帳
分裂エピックと分裂モニック (split epic / monic)

分裂エピック
定義
ある射 \(f\) が圏 \(\mathscr{C}\) で分裂エピック (split epic) であるとは、
\[
q {\sf \, ⨟ \,} f = {\rm id}_{{\rm cod}(f)}
\]
を満たすような射 \(q\) が圏 \(\mathscr{C}\) に存在することをいう。
現段階では一階述語論理の上で公理的に圏を取り扱っているので、それに準拠したフォーマルな書き方をすると
\[
{\rm isSplitEpic}(f) :\Leftrightarrow \exists q [\exists h[{\rm \_comp}(q,f,h) \wedge {\rm \_cod}(f,h)]]
\]
が真であるとき、\(f\) が圏 \(\mathscr{C}\) で分裂エピックであるということになる。
またこの時、そのような射 \(q\) のことを「\(f\) のセクション (section)」 (または断面) と呼ぶ。
わかりやすく言い換えれば、射 \(f\) のセクションが圏 \(\mathscr{C}\) に存在するとき、\(f\) が圏 \(\mathscr{C}\) で分裂エピックということになる。
わかりやすく言い換えれば、射 \(f\) のセクションが圏 \(\mathscr{C}\) に存在するとき、\(f\) が圏 \(\mathscr{C}\) で分裂エピックということになる。
余談
「右逆射」という言葉を避けて「セクション」や「断面」という呼称を使用しているのは、ここでは射の合成を「図式オーダー」で記述しているためである。
図式オーダーを採用していることにより、見て通り数式上での左右が真逆となっているため、「"右" 逆射」という言葉を使うのは余計な混乱を招きかねない。
一般的抽象的ナンセンス
分裂エピックはエピック
(周囲圏を任意の圏 \(\mathscr{C}\) とする。)
\(f\) を分裂エピック射、\(q\) を \(f\) の任意のセクションとする。
まず、任意の射 \(h,k\) について次の関係式
まず、任意の射 \(h,k\) について次の関係式
\[
f {\sf \, ⨟ \,} h = f {\sf \, ⨟ \,} k
\]
が成り立っている状況を考えると、
\[
\begin{align}
f {\sf \, ⨟ \,} h &= f {\sf \, ⨟ \,} k \\
q {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} h) &= q {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} k) \\
(q {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} h &= (q {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} k \\
{\rm id}_{{\rm cod}(f)} {\sf \, ⨟ \,} h &= {\rm id}_{{\rm cod}(f)} {\sf \, ⨟ \,} k \\
h &= k \\
\end{align}
\]
よって
\[
(f {\sf \, ⨟ \,} h = f {\sf \, ⨟ \,} k) \Rightarrow (h = k)
\]
が任意の \(h,k\) について成立するというエピックの定義が満たされる。
具体例
区間圏の持つ非自明な射は分裂エピックでない
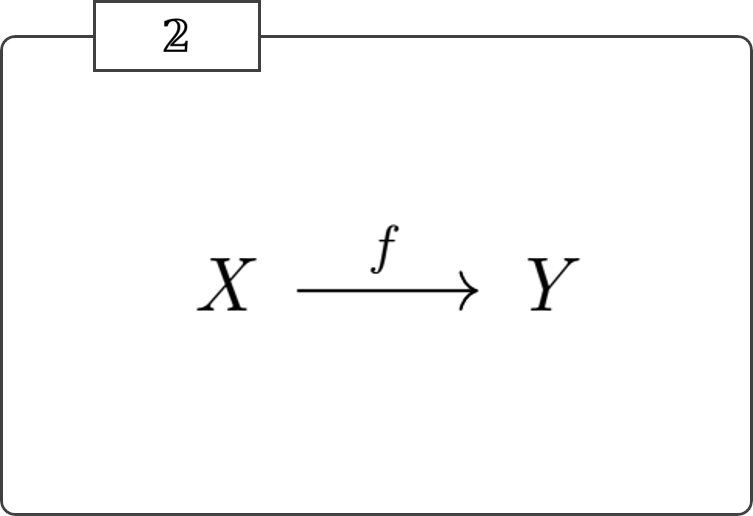
上に示した区間圏の持つ非自明な射 \(f:X\rightarrow Y\) は分裂エピックでない。
これについても、前回同様コンピュータに愚直に調べてもらうことができて、
ghci> isSplitEpic(Arr_f)
Falseというように「分裂エピックでない」という結果を出力する。
余談
敢えて機械的に調べるまでもなく、圏の全体像を見れば「\(f\) に対して逆を向く矢印が区間圏の中にそもそもとして存在していない」ということから直ちに分裂エピックには成り得ないことは予想できる。
もちろん、対象 \(X:X\rightarrow X\) は一般的に示されるように、コンピュータで機械的に調べても
ghci> isSplitEpic(Obj_X)
Trueというように、「分裂エピックである」という結果になる。
分裂モニック
定義
ある射 \(f\) が圏 \(\mathscr{C}\) で分裂モニック (split monic) であるとは、
\[
f {\sf \, ⨟ \,} q = {\rm id}_{{\rm dom}(f)}
\]
を満たすような射 \(q\) が圏 \(\mathscr{C}\) に存在することをいう。
現段階では一階述語論理の上で公理的に圏を取り扱っているので、それに準拠したフォーマルな書き方をすると
\[
{\rm isSplitMonic}(f) :\Leftrightarrow \exists q [\exists h[{\rm \_comp}(f,q,h) \wedge {\rm \_dom}(f,h)]]
\]
が真であるとき、\(f\) が圏 \(\mathscr{C}\) で分裂モニックであるということになる。
またこの時、そのような射 \(q\) のことを「\(f\) のレトラクション (retraction)」と呼ぶ。
わかりやすく言い換えれば、射 \(f\) のレトラクションが圏 \(\mathscr{C}\) に存在するとき、\(f\) が圏 \(\mathscr{C}\) で分裂モニックということになる。
わかりやすく言い換えれば、射 \(f\) のレトラクションが圏 \(\mathscr{C}\) に存在するとき、\(f\) が圏 \(\mathscr{C}\) で分裂モニックということになる。
一般的抽象的ナンセンス
分裂モニックはモニック
(周囲圏を任意の圏 \(\mathscr{C}\) とする。)
\(f\) を分裂モニック射、\(q\) を \(f\) の任意のレトラクションとする。
まず、任意の射 \(h,k\) について次の関係式
まず、任意の射 \(h,k\) について次の関係式
\[
h {\sf \, ⨟ \,} f = k {\sf \, ⨟ \,} f
\]
が成り立っている状況を考えると、
\[
\begin{align}
h {\sf \, ⨟ \,} f &= k {\sf \, ⨟ \,} f \\
(h {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} q &= (k {\sf \, ⨟ \,} f) {\sf \, ⨟ \,} q \\
h {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} q) &= k {\sf \, ⨟ \,} (f {\sf \, ⨟ \,} q) \\
h {\sf \, ⨟ \,} {\rm id}_{{\rm dom}(f)} &= k {\sf \, ⨟ \,} {\rm id}_{{\rm dom}(f)} \\
h &= k \\
\end{align}
\]
よって
\[
(h {\sf \, ⨟ \,} f = k {\sf \, ⨟ \,} f) \Rightarrow (h = k)
\]
が任意の \(h,k\) について成立するというモニックの定義が満たされる。
双対性
これら2つの圏論的な概念が圏論的双対で結ばれている
つまり以下のようなマクロ置換を考える
- \({\rm \_comp}(f,g,h)\) を \({\rm \_comp}(g,f,h)\)
- \({\rm \_dom}(f,h)\) を \({\rm \_cod}(f,h)\)
- \({\rm \_cod}(f,h)\) を \({\rm \_dom}(f,h)\)
実際にやってみると、分裂エピックの定義
\[
\exists q [\exists h[{\rm \_comp}(q,f,h) \wedge {\rm \_cod}(f,h)]]
\]
は
\[
\exists q [\exists h[{\rm \_comp}(f,q,h) \wedge {\rm \_dom}(f,h)]]
\]
となり、分裂モニックの定義が得られ、逆に分裂モニックの定義からは分裂エピックの定義が得られる。
おまけ
分裂エピック・分裂モニックの愚直な判定に用いた Haskell コード
class Eq a => (FiniteCategory a) where
listOfData :: [a]
domR :: (a,a) -> Bool
codR :: (a,a) -> Bool
compR :: (a,a,a) -> Bool
-- 区間圏
data IntervalCat = Obj_X | Obj_Y | Arr_f deriving Eq
instance FiniteCategory IntervalCat where
listOfData = [Obj_X, Obj_Y, Arr_f]
domR (arrow1, arrow2) =
case (arrow1, arrow2) of
(Obj_X, Obj_X) -> True
(Arr_f, Obj_X) -> True
(Obj_Y, Obj_Y) -> True
_ -> False
codR (arrow1, arrow2) =
case (arrow1, arrow2) of
(Obj_X, Obj_X) -> True
(Obj_Y, Obj_Y) -> True
(Arr_f, Obj_Y) -> True
_ -> False
compR (arrow1, arrow2, arrow3) =
case (arrow1, arrow2, arrow3) of
(Obj_X, Obj_X, Obj_X) -> True
(Obj_X, Arr_f, Arr_f) -> True
(Obj_Y, Obj_Y, Obj_Y) -> True
(Arr_f, Obj_Y, Arr_f) -> True
_ -> False
-- 特に深い意味のない圏1
data Cat_NS1 =
CatNS1_X1 | CatNS1_X2 | CatNS1_X3 | CatNS1_X4 | CatNS1_X5 | CatNS1_X6 |
CatNS1_X7 | CatNS1_X8 | CatNS1_X9 | CatNS1_X10 | CatNS1_X11 | CatNS1_X12 |
CatNS1_f'1_2' | CatNS1_f'1_4' | CatNS1_f'1_7' | CatNS1_f'1_11' |
CatNS1_f'3_2' | CatNS1_f'3_6' | CatNS1_g'3_6' |
CatNS1_f'4_2' | CatNS1_g'4_2' |
CatNS1_f'5_8' | CatNS1_f'5_10' | CatNS1_f'5_12' |
CatNS1_f'6_2' |
CatNS1_f'7_11' |
CatNS1_f'9_2' | CatNS1_f'9_6' | CatNS1_f'9_11' | CatNS1_f'9_12'
deriving (Show,Eq)
instance FiniteCategory Cat_NS1 where
listOfData =
[ CatNS1_X1 , CatNS1_X2 , CatNS1_X3 , CatNS1_X4 , CatNS1_X5 , CatNS1_X6
, CatNS1_X7 , CatNS1_X8 , CatNS1_X9 , CatNS1_X10 , CatNS1_X11 , CatNS1_X12
, CatNS1_f'1_2' , CatNS1_f'1_4' , CatNS1_f'1_7' , CatNS1_f'1_11'
, CatNS1_f'3_2' , CatNS1_f'3_6' , CatNS1_g'3_6'
, CatNS1_f'4_2' , CatNS1_g'4_2'
, CatNS1_f'5_8' , CatNS1_f'5_10' , CatNS1_f'5_12'
, CatNS1_f'6_2'
, CatNS1_f'7_11'
, CatNS1_f'9_2' , CatNS1_f'9_6' , CatNS1_f'9_11' , CatNS1_f'9_12' ]
domR (arrow1, arrow2) =
case (arrow1, arrow2) of
(CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12) -> True
(CatNS1_f'1_2', CatNS1_X1) -> True
(CatNS1_f'1_4', CatNS1_X1) -> True
(CatNS1_f'1_7', CatNS1_X1) -> True
(CatNS1_f'1_11', CatNS1_X1) -> True
(CatNS1_f'3_2', CatNS1_X3) -> True
(CatNS1_f'3_6', CatNS1_X3) -> True
(CatNS1_g'3_6', CatNS1_X3) -> True
(CatNS1_f'4_2', CatNS1_X4) -> True
(CatNS1_g'4_2', CatNS1_X4) -> True
(CatNS1_f'5_8', CatNS1_X5) -> True
(CatNS1_f'5_10', CatNS1_X5) -> True
(CatNS1_f'5_12', CatNS1_X5) -> True
(CatNS1_f'6_2', CatNS1_X6) -> True
(CatNS1_f'7_11', CatNS1_X7) -> True
(CatNS1_f'9_2', CatNS1_X9) -> True
(CatNS1_f'9_6', CatNS1_X9) -> True
(CatNS1_f'9_11', CatNS1_X9) -> True
(CatNS1_f'9_12', CatNS1_X9) -> True
_ -> False
codR (arrow1, arrow2) =
case (arrow1, arrow2) of
(CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12) -> True
(CatNS1_f'1_2', CatNS1_X2) -> True
(CatNS1_f'1_4', CatNS1_X4) -> True
(CatNS1_f'1_7', CatNS1_X7) -> True
(CatNS1_f'1_11', CatNS1_X11) -> True
(CatNS1_f'3_2', CatNS1_X2) -> True
(CatNS1_f'3_6', CatNS1_X6) -> True
(CatNS1_g'3_6', CatNS1_X6) -> True
(CatNS1_f'4_2', CatNS1_X2) -> True
(CatNS1_g'4_2', CatNS1_X2) -> True
(CatNS1_f'5_8', CatNS1_X8) -> True
(CatNS1_f'5_10', CatNS1_X10) -> True
(CatNS1_f'5_12', CatNS1_X12) -> True
(CatNS1_f'6_2', CatNS1_X2) -> True
(CatNS1_f'7_11', CatNS1_X11) -> True
(CatNS1_f'9_2', CatNS1_X2) -> True
(CatNS1_f'9_6', CatNS1_X6) -> True
(CatNS1_f'9_11', CatNS1_X11) -> True
(CatNS1_f'9_12', CatNS1_X12) -> True
_ -> False
compR (arrow1, arrow2, arrow3) =
case (arrow1, arrow2, arrow3) of
(CatNS1_X1, CatNS1_X1, CatNS1_X1) -> True
(CatNS1_X2, CatNS1_X2, CatNS1_X2) -> True
(CatNS1_X3, CatNS1_X3, CatNS1_X3) -> True
(CatNS1_X4, CatNS1_X4, CatNS1_X4) -> True
(CatNS1_X5, CatNS1_X5, CatNS1_X5) -> True
(CatNS1_X6, CatNS1_X6, CatNS1_X6) -> True
(CatNS1_X7, CatNS1_X7, CatNS1_X7) -> True
(CatNS1_X8, CatNS1_X8, CatNS1_X8) -> True
(CatNS1_X9, CatNS1_X9, CatNS1_X9) -> True
(CatNS1_X10, CatNS1_X10, CatNS1_X10) -> True
(CatNS1_X11, CatNS1_X11, CatNS1_X11) -> True
(CatNS1_X12, CatNS1_X12, CatNS1_X12) -> True
(CatNS1_X1, CatNS1_f'1_2', CatNS1_f'1_2') -> True
(CatNS1_X1, CatNS1_f'1_4', CatNS1_f'1_4') -> True
(CatNS1_X1, CatNS1_f'1_7', CatNS1_f'1_7') -> True
(CatNS1_X1, CatNS1_f'1_11', CatNS1_f'1_11') -> True
(CatNS1_X3, CatNS1_f'3_2', CatNS1_f'3_2') -> True
(CatNS1_X3, CatNS1_f'3_6', CatNS1_f'3_6') -> True
(CatNS1_X3, CatNS1_g'3_6', CatNS1_g'3_6') -> True
(CatNS1_X4, CatNS1_f'4_2', CatNS1_f'4_2') -> True
(CatNS1_X4, CatNS1_g'4_2', CatNS1_g'4_2') -> True
(CatNS1_X5, CatNS1_f'5_8', CatNS1_f'5_8') -> True
(CatNS1_X5, CatNS1_f'5_10', CatNS1_f'5_10') -> True
(CatNS1_X5, CatNS1_f'5_12', CatNS1_f'5_12') -> True
(CatNS1_X6, CatNS1_f'6_2', CatNS1_f'6_2') -> True
(CatNS1_X7, CatNS1_f'7_11', CatNS1_f'7_11') -> True
(CatNS1_X9, CatNS1_f'9_2', CatNS1_f'9_2') -> True
(CatNS1_X9, CatNS1_f'9_6', CatNS1_f'9_6') -> True
(CatNS1_X9, CatNS1_f'9_11', CatNS1_f'9_11') -> True
(CatNS1_X9, CatNS1_f'9_12', CatNS1_f'9_12') -> True
(CatNS1_f'1_2', CatNS1_X2, CatNS1_f'1_2') -> True
(CatNS1_f'1_4', CatNS1_X4, CatNS1_f'1_4') -> True
(CatNS1_f'1_7', CatNS1_X7, CatNS1_f'1_7') -> True
(CatNS1_f'1_11', CatNS1_X11, CatNS1_f'1_11') -> True
(CatNS1_f'3_2', CatNS1_X2, CatNS1_f'3_2') -> True
(CatNS1_f'3_6', CatNS1_X6, CatNS1_f'3_6') -> True
(CatNS1_g'3_6', CatNS1_X6, CatNS1_g'3_6') -> True
(CatNS1_f'4_2', CatNS1_X2, CatNS1_f'4_2') -> True
(CatNS1_g'4_2', CatNS1_X2, CatNS1_g'4_2') -> True
(CatNS1_f'5_8', CatNS1_X8, CatNS1_f'5_8') -> True
(CatNS1_f'5_10', CatNS1_X10, CatNS1_f'5_10') -> True
(CatNS1_f'5_12', CatNS1_X12, CatNS1_f'5_12') -> True
(CatNS1_f'6_2', CatNS1_X2, CatNS1_f'6_2') -> True
(CatNS1_f'7_11', CatNS1_X11, CatNS1_f'7_11') -> True
(CatNS1_f'9_2', CatNS1_X2, CatNS1_f'9_2') -> True
(CatNS1_f'9_6', CatNS1_X6, CatNS1_f'9_6') -> True
(CatNS1_f'9_11', CatNS1_X11, CatNS1_f'9_11') -> True
(CatNS1_f'9_12', CatNS1_X12, CatNS1_f'9_12') -> True
(CatNS1_f'1_4', CatNS1_f'4_2', CatNS1_f'1_2') -> True
(CatNS1_f'1_4', CatNS1_g'4_2', CatNS1_f'1_2') -> True
(CatNS1_f'1_7', CatNS1_f'7_11', CatNS1_f'1_11') -> True
(CatNS1_f'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True
(CatNS1_g'3_6', CatNS1_f'6_2', CatNS1_f'3_2') -> True
(CatNS1_f'9_6', CatNS1_f'6_2', CatNS1_f'9_2') -> True
_ -> False
-- 分裂エピックか否かの判定式
isSplitEpic :: (FiniteCategory a) => a -> Bool
isSplitEpic f =
_exists'(\q -> _exists'(\h -> compR(q,f,h) && codR(f,h)))
where
_forall' p = _forall(listOfData, p)
_exists' p = _exists(listOfData, p)
-- 分裂モニックか否かの判定式
isMonic :: (FiniteCategory a) => a -> Bool
isMonic f =
_forall'(\h -> _forall'(\k -> _exists'(\l -> compR(h,f,l) && compR(k,f,l)) `implies` (h == k)))
where
_forall' p = _forall(listOfData, p)
_exists' p = _exists(listOfData, p)
isSplitMonic :: (FiniteCategory a) => a -> Bool
isSplitMonic f =
_exists'(\q -> _exists'(\h -> compR(f,q,h) && domR(f,h)))
where
_forall' p = _forall(listOfData, p)
_exists' p = _exists(listOfData, p)
_forall :: ([a], (a -> Bool)) -> Bool
_forall (dat,_P) = and (fmap _P $ dat)
_exists :: ([a], (a -> Bool)) -> Bool
_exists (dat,_P) = or (fmap _P $ dat)
implies x y = (not x) || yタグ一覧:
