雑記帳
写像に終域は必要ない?
前置き
まず「終域」って何?という場合用に以下にリンクを貼っておく。
- 終域 (Wikipedia 記事)
(圏論をやっている人にとっては、「終域」ではなく「コドメイン」という呼称の方が馴染み深いだろうか)
そもそも写像の定義とは?
ZFC 集合論の場合...
ZFC 集合論においては、写像は通常「値の対応の規則をまとめた対応表 (写像のグラフ)」として定義されるのだが、ここで ZFC は物質的集合論であり、集合を形あるモノ (substance) として扱うことができてしまう。
余談
写像の集合構成を「写像のグラフ単品」ではなく、定義域と終域を含めた3つ組として定義する流儀もある。
つまり例えば
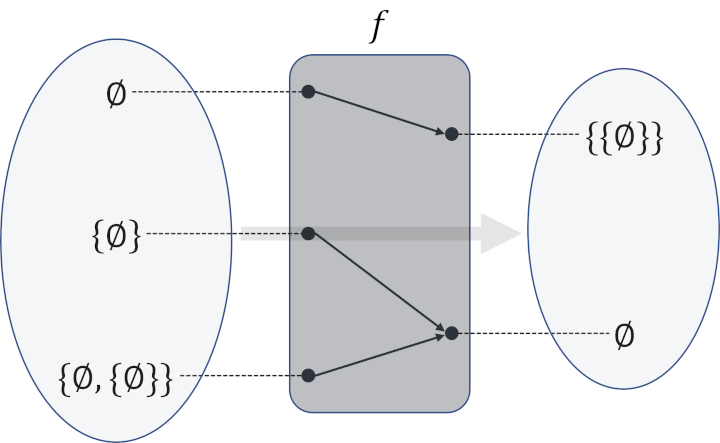
\[
\begin{align}
f(\varnothing) &= \{\{\varnothing\}\} \\
f(\{\varnothing\}) &= \varnothing \\
f(\{\varnothing,\{\varnothing\}\}) &= \varnothing \\
\end{align}
\]
という集合同士の対応が与えられれば
- 「好きな集合 \(X\) とその好きな集合に対応させたい任意の集合 \(Y\) のペア \(\langle X,Y \rangle\)」 たちを要素に持つ集合
という形でその写像 \(f\) のグラフ \(\Gamma_f\) を構成することができる。
具体的には
\[
\begin{align}
\langle X_1,X_2 \rangle &:= \{\{X_1\},\{X_1,X_2\}\} \\
\end{align}
\]
としたとき、
\[
\begin{align}
\Gamma_f = & \{ \langle \varnothing, \{\{\varnothing\}\} \rangle \\
&, \langle \{\varnothing\}, \varnothing \rangle \\
&, \langle \{\varnothing,\{\varnothing\}\}, \varnothing \rangle \} \\
\end{align}
\]
と構成できる。
この集合を見ての通り、「対応先が定義された集合全体 (定義域)」
\[
\{ \varnothing, \{\varnothing\}, \{\varnothing\,\{\varnothing\}\} \}
\]
と「対応させる値全体の集合 (値域)」
\[
\{ \{\{\varnothing\}\}, \varnothing \}
\]
の情報は写像のグラフから一意に取り出せる情報であるが、見ての通り決まった「終域」の情報はこの対応の規則からは見出せない。
それ故か、物質的集合論の世界観を重視する人からはしばしば、「終域は必要ない」と見做される傾向があるように思える。
ETCS 集合論の場合...
ETCS 集合論においては「特定の性質を満たす圏の持つ矢印」のことを「写像」と呼んでいるため、写像の終域は原理的に切り離せない。
つまるところ ETCS において「写像に終域は必要ない」というのは「矢印に先端は必要ない」と言っているのと同じことなので、これがかなりぶっ飛んだ主張であることは明らかだと思う。
因みに ETCS は構造的集合論であり、集合の内部構造を落とした抽象集合を扱うことになるため、ZFC の節で行ったような方法と全く同じようにして写像を定義することはできなくなる。
ということもあり、構造的集合論の世界観を重視する場合は逆に、「終域は不可欠」と見做されることになる。
「平方をとる関数がどのようにして定義されるのか」を具体的に比較することで、2つのタイプの集合論の違いをみる
ZFC 集合論の場合...
ZFC のような物質的集合論においては、基本的に
\[
{\rm sq}(n) = n \times n
\]
で済む。
より具体的に、冒頭で述べた通り ZFC においては「写像のグラフ」を写像の集合構成として与えるのだが、以下のようにして写像 \({\rm sq}\) のグラフ
\[
\Gamma_{\rm sq} = \{ z\in {\mathbb{N}}\times {\mathbb{N}} \:|\: \exists n[ n\in {\mathbb{N}} \wedge (z = \langle n, n\times n \rangle)] \}
\]
を具体集合として組み立てることができる。
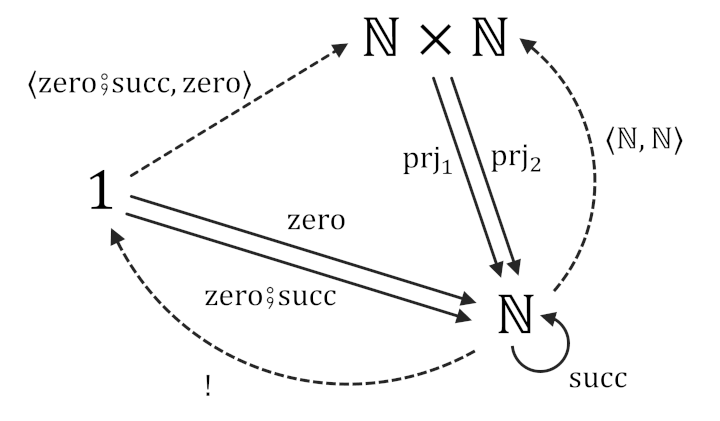
ETCS 集合論の場合...
ETCS において写像は「与えられている公理を用いた演繹によって構成される矢印」であり、この例の場合は
- 入力を2つにコピーする写像
- 2つの自然数の積をとる写像
という2つの写像の合成射
\[
{\rm sq} = \langle {\mathbb{N}},{\mathbb{N}} \rangle {\sf \, ⨟ \,} (({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\rm const}({\rm zero})),\lambda[\langle {\rm ev}, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\mathbb{N}}),\lambda[{\rm ev} {\sf \, ⨟ \,} {\rm succ}])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev}) ])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev})
\]
として構成する必要がある。
ZFC のように平方を定義する場合は終域が自動的に定まらないが、見ての通り ETCS の場合は構成される写像が必ず決まった終域を持つ。
確認してみればわかるように、この構成方法として与えられる平方関数の終域は \({\mathbb{N}}\) となっている。
因みに、\({\mathbb{N}}\) のある部分集合 \(\langle S,i \rangle\) が与えられたとし、それが
\[
{\rm sq} {\sf \, ⨟ \,} \chi[i] = !{\sf \, ⨟ \,} {\rm true}
\]
を満たすのであれば、引き戻しの普遍性から引き起こされる射として、「終域をその部分集合に狭めたバージョンの平方関数 \({\mathbb{N}}\rightarrow S\)」を得ることも可能である。
例えば、\({\rm sq}\) の像 \(\langle {\rm Im}({\rm sq}), j \rangle\) から、全単射 \(h:{\mathbb{N}}\rightarrow {\rm Im}({\rm sq})\) が得られる。
一応補足しておくと、ETCS でも ZFC で構成したような写像のグラフを \({\mathbb{N}} \times {\mathbb{N}}\) の部分集合として構成できるが、置換公理型が認められない以上、その部分集合の構成に必要になる射 \({\mathbb{N}} \times {\mathbb{N}} \rightarrow \Omega\) を導くために上の \({\rm sq}\) が先行して必要になってしまう。つまるところ「\({\rm sq}\) を定義する」という目標を達成するために、わざわざ写像のグラフを構成するという手順を踏む意味がまるでない。
余談
引き起こされる射 \(h\) と 大本の写像 \({\rm sq}\) は ETCS の観点からは、明確に異なるものとして扱われる。
一方で、ZFC の観点からは、技術的にはそれらを同一の写像と考えてしまうことすら可能である。
一方で、ZFC の観点からは、技術的にはそれらを同一の写像と考えてしまうことすら可能である。
タグ一覧:
