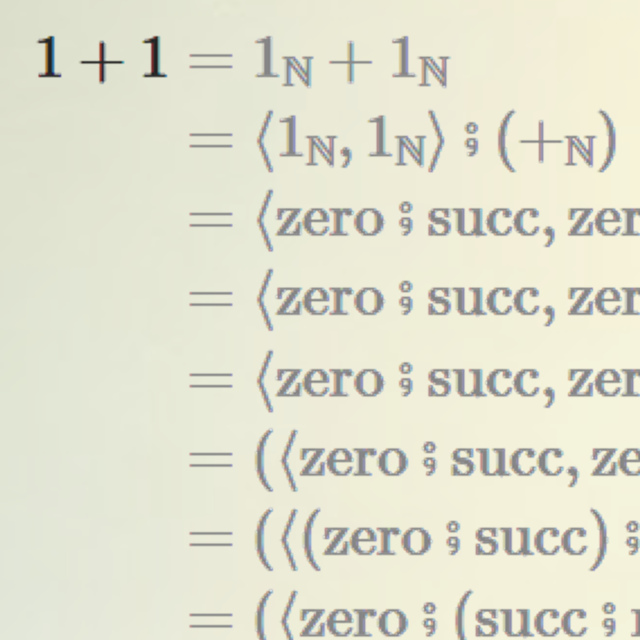雑記帳
再帰を圏論的に定式化する 【自然数対象 (natural numbers object)】
自然数対象 (natural numbers object)
導入
(...)
定義
トポス \(\mathscr{C}\) を周囲圏に考えるとき
- 自然数対象 \({\mathbb{N}}\)
- 自然数対象の一点 \({\rm zero}:1\rightarrow {\mathbb{N}}\)
- サクセッサー \({\rm succ}:{\mathbb{N}} \rightarrow {\mathbb{N}}\)
は、
- \(X\) を任意の対象
- \(x_0\) を対象 \(X\) の任意の一点
- \(f\) を \(X\) 上の任意の自己準同形 \(f:X\rightarrow X\)
としたとき、以下の図式を可換にするような一意的な射 \({\rm rec}_{{\mathbb{N}}}(x_0,f)\) が常に存在することとして定義される。
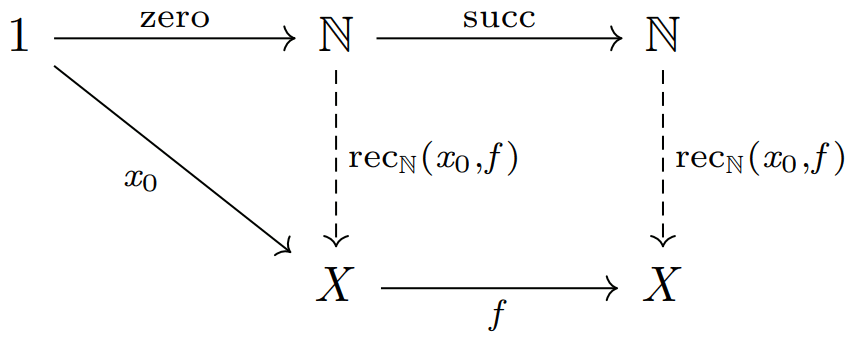
(...)
余談
周囲圏に「トポス」を考えなくても「カルテシアン閉圏」を想定すれば、大域要素 \(x:1\rightarrow X\) を \(X\) の要素として正しく解釈できるし、後に説明する「自然数の間の加法や乗法」も厳密に定義することは可能である。
トポスを想定している理由は、自然数の順序の構成にトポスの持つ論理演算が必要になるためである。
トポスを想定している理由は、自然数の順序の構成にトポスの持つ論理演算が必要になるためである。
一階の言語による定義
(...)
説明
(...)
図式を見れば明らかなように、\({\rm rec}_{{\mathbb{N}}}(x_0,f)\) は自然数 \(n\) の入力に対して、「自己準同形 \(f\) の自身との \(n\) 回の合成により得られる射に \(x_0\) を入力して得られる出力」を出力する射としての意味を持つ。
自然数対象に関する重要な射の構成
自然数同士の足し算
よって加法 \((+_{{\mathbb{N}}}):{\mathbb{N}} \times {\mathbb{N}} \rightarrow {\mathbb{N}}\) は次のように構成される。
\[
(+_{{\mathbb{N}}}) := ({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\mathbb{N}}),\lambda[{\rm ev} {\sf \, ⨟ \,} {\rm succ}])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev}
\]
このようにして構成される射が実際に足し算として機能することを実感してもらえるように、以下の記事で「1+1 が 2 になるまでの流れ」も具体例として紹介している。
もし、この定義に対する不信感が拭えない場合は是非参考にしてほしい。
自然数同士の掛け算
よって乗法 \((\cdot_{{\mathbb{N}}}):{\mathbb{N}} \times {\mathbb{N}} \rightarrow {\mathbb{N}}\) は次のように構成される。
\[
(\cdot_{{\mathbb{N}}}) := ({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\rm const}({\rm zero})),\lambda[\langle {\rm ev}, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_{{\mathbb{N}}}) ])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev}
\]
自然数の平方
よって平方 \({\rm sq}_{{\mathbb{N}}}:{\mathbb{N}} \rightarrow {\mathbb{N}}\) は次のように構成される。
\[
{\rm sq}_{{\mathbb{N}}} := \Delta {\sf \, ⨟ \,} (\cdot_{{\mathbb{N}}})
\]
自然数の階乗
よって階乗 \((!_{{\mathbb{N}}}):{\mathbb{N}} \rightarrow {\mathbb{N}}\) は次のように構成される。
\[
(!_{{\mathbb{N}}}) := ({\rm rec}_{{\mathbb{N}}}(\langle {\rm zero},{\rm zero} {\sf \, ⨟ \,} {\rm succ} \rangle, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, ({\rm succ} \times {\mathbb{N}}) {\sf \, ⨟ \,} (\cdot_{{\mathbb{N}}}) \rangle){\sf \, ⨟ \,} {\rm prj}_2
\]
自然数の間の順序1
\[
m \le n :\Leftrightarrow \exists x:{\mathbb{N}}[m+x==n]
\]
よって順序 \((\le_{{\mathbb{N}}}):{\mathbb{N}} \times {\mathbb{N}} \rightarrow \Omega\) は次のように構成される。
\[
(\le_{{\mathbb{N}}}) := \lambda[\Delta {\sf \, ⨟ \,} ((\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_{{\mathbb{N}}}))\times({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2)) {\sf \, ⨟ \,} (==)] {\sf \, ⨟ \,} (\exists_{{\mathbb{N}}})
\]
また、\((\exists_{{\mathbb{N}}})\) 等の論理演算子に関する射の定義については「置換公理型を認めない初等トポスの一般論の中で、集合 {x∈X|P(x)} はどのようにして構成されるのか」を参照。
自然数の間の順序2
\[
m < n :\Leftrightarrow (m{\sf \, ⨟ \,} {\rm succ}) \le n
\]
よって順序 \((<_{{\mathbb{N}}}):{\mathbb{N}} \times {\mathbb{N}} \rightarrow \Omega\) は次のように構成される。
\[
(<_{{\mathbb{N}}}) := ({\rm succ} \times {\mathbb{N}}) {\sf \, ⨟ \,} (\le_{{\mathbb{N}}})
\]
記述されている情報にもう少し確証が欲しい場合...
自然数対象は数学概念の一つであり、そうである以上、どこの説明も本質的には同じ定義となっているはずだが、情報源が一つだけではそのことの確かめようがない。
ということで、その辺を確認したい人にとって参考になりそうなリンクを以下に貼っておく。
- natural numbers object (nLab 記事)
- Natural numbers object (Wikipedia 記事)
タグ一覧: