雑記帳
線形空間 V,W のテンソル積 V⊗W

まずここで基礎として仮定しているのは、Propositional resizing 公理を認めるホモトピー型理論で、特にその上で定式化される (集合の圏を使った) 集合論を意識して記述している。(Propositional resizing 公理から排中律が従い、さらに排中律によって集合の圏が well-pointed トポスとなることが従うため、「選択公理を除いた ETCS」という形で集合論を展開することができる。ちなみにここでも ETCS スタイルで集合の記述が行われているのはそれが理由となっている。)
定義
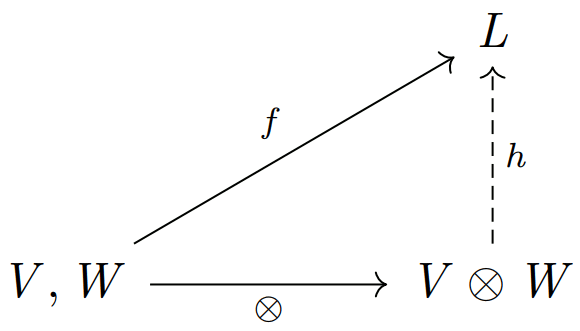
\(K\)-線形空間 \(V,W\) が与えられているとき、\(V\) と \(W\) の テンソル積 (tensor product) \(V\otimes W\) とは、ある一つの普遍的な双線形写像 \(\otimes:V,W\rightarrow V\otimes W\) があって、また、任意の双線形写像 \(f:V,W\rightarrow L\) が与えられたとき、\(f\) がその普遍 (\(f\) の選択に依らない) 双線形写像 \(\otimes\) と何らかの線形写像 \(h:V\otimes W\rightarrow L\) との合成の形に分解可能で、またその \(h\) が一意的となる (\(f=\otimes {\sf \, ⨟ \,} h\) を満たす \(h\) が一意に存在する) といった条件を満たす普遍射を伴う \(K\)-線形空間 \(V\otimes W\) という定義がわかりやすい。
余談
ここでは圏論的な視点にウェイトを置いているため、双線形写像の記号は「単なる線形写像と見間違いやすい記号 \(f:V\times W\rightarrow L\)」ではなく「多重圏の射としての記号 \(f:V,W\rightarrow L\)」の方を採用している。
基底を使った定義は簡単である一方で
- 基底の存在を仮定できないより抽象的なケースに対応できない。
- 具体集合ではなく抽象集合を理論の構成要素として扱うというここでの都合上、「特定の意味を持った記号からなる具体集合の構成」という操作がそもそも無造作にできない。
といった理由からここでは汎用性の高い定義の方でテンソル積の概念を導入する。
テンソル積の構成
集合論的な構成方法
まずは集合論的なテンソル積 \(V\otimes W\) の構成法について。(但し集合論的とはいっても、言語としての圏論の力は借りている。)
定義を見ての通り、双線形写像の decomposition を考えたいので、まずは根本に戻って双線形写像の定義となっている式を振り返る。
余談
この「テンソル積の構成」については僕自身学生の時に結構悩んだ部分なので、かなりくどいほど線形空間と線形空間の基底集合とを区別して説明をしている。
言うなればこの記事は、「テンソル積の理解に悩んでいた頃の僕自身が欲しかった解説 (当時から厳密さに執着していた僕に向けた解説)」であります。
通常の双線形写像の定義のおさらい
まず
- \(K\): 体 (\(\text{uSetOf}(K)\) を \(K\) の基底集合, \(+_{K}\) を \(K\) の持つ加法, \(\cdot_{K}\) を \(K\) の持つ乗法とする)
- \(V,W,L\): \(K\)-線形空間 (\(\text{uSetOf}(V)\) を \(V\) の基底集合, \(+_{V}\) を \(V\) の持つ加法, \(\cdot_{V}\) を \(V\) の持つスカラー倍とする)
- \(U\): \(V\) に 基底集合 \(\text{uSetOf}(V)\) を対応させ、線形空間の圏の持つ抽象的な矢印 \(f\) に「元になっている基底集合間の写像 \(g\)」を対応させる忘却関手 \(\mathbf{Vect}_K \rightarrow \mathbf{Set}\)
- \(F\): \(E\) に 自由線形空間 \(K\{E\}\) を対応させ、写像 \(f\) に「自由対象の普遍性から引き起こされる線形空間の圏の持つ射 \(g\)」を対応させる自由関手 \(\mathbf{Set}\rightarrow \mathbf{Vect}_K\)
としたとき、双線形写像 \(f:V,W\rightarrow L\) は写像 \(f':U(V\times W)\rightarrow U(L)\) の内、以下の条件を満たすものとして定義できる。
任意の \(x,x':1\rightarrow U(V)\)、\(y,y':1\rightarrow U(W)\)、\(a:1\rightarrow \text{uSetOf}(K)\) に対して
\[
\begin{align}
f'(x,y)+_{L}f'(x',y)&=f'(x+_{V}x',y) \\
f'(x,y)+_{L}f'(x,y')&=f'(x,y+_{W}y') \\
a\cdot_{L} f'(x,y)&=f'(a\cdot_{V} x,y) \\
a\cdot_{L} f'(x,y)&=f'(x,a\cdot_{W} y) \\
\end{align}
\]
見ての通りこの定義では、双線形写像 \(f:V,W\rightarrow U\) は特別な性質を満たす写像 \(U(V\times W)\rightarrow U(L)\) として与えられる。
この定義を見れば気付くかもしれないが、普遍性を考えていく上で一つの大きな障壁がある。
冒頭で述べたテンソル積の普遍性からわかるように、引き起こされる射が「線形空間の間を結ぶ射」であるわけだから、その普遍性は線形空間の圏の中でそのまま議論されるものだと期待したくなる。しかし残念ながら根本的に「双線形写像は線形空間の圏の射ではない」という問題がある。
普遍性を考察していく上で「どの圏で議論しているのか」ということが明らかになっていなければまず話にならないわけだが、「双線形写像がどの圏の射であるのか」という肝心なことすらはっきりしていないというのが現状となっている。
余談
先ほどの補足でも触れたが、多重圏の概念を導入することで圏論的に双線形写像たちをそれぞれ圏の中の一つの射の形に落とし込むことはできる。但しここでは多重圏の概念を直接的に持ち出すことなくテンソル積の構成を進めていく方針をとる。
とはいっても、「双線形写像に相当する線形写像」なるものさえ導入することができれば、テンソル積の普遍性を「線形空間の圏」の中で議論できるような気がしないだろうか。(「集合の圏」ではダメなのかと思うかもしれないが、「引き起こされる射」は「線形空間の間を結ぶ射」であるわけだから、「集合の圏」ではなく「線形空間の圏」で考えた方が断然都合がよい。)
テンソル積の普遍性を線形空間の圏の中で議論できるようにする
そのためには、まず第一に「一般的な写像 (集合の間を結ぶ射)」を「線形空間の間を結ぶ射」として表すことができなければ話が進まないわけであるが、これに関しては、具体圏である線形空間の圏に付随する集合の圏への通常の忘却関手に関する自由対象の構成を許すという点に注目することで解決する。
具体的には、随伴関手に関する有名な同形
\[
\hom_{\mathbf{Set}}(U(V\times W),U(L)) \cong \hom_{\mathbf{Vect}_K}(F(U(V\times W)),L)
\]
から、その「集合の間を結ぶ射と線形空間の間を結ぶ射とが相互に結びつけられる事実」を見て取ることができる。
では本題に戻る。まず自由対象の普遍性
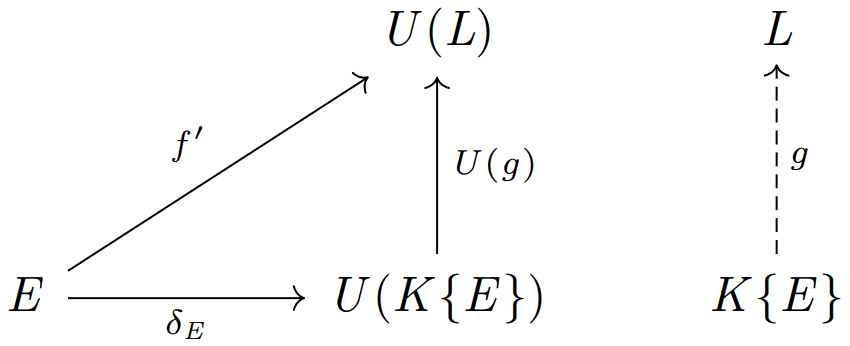
より、任意の写像 \(f':U(V\times W)\rightarrow U(L)\) が与えられると、
\[
f' = \delta_{U(V\times W)} {\sf \, ⨟ \,} U(g)
\]
と一意に分解できるような線形空間の圏の射 \(g:K\{U(V\times W)\}\rightarrow L\) の存在が従う。
また、写像 \(U(g)\) は忘却関手によって線形空間の圏にある射を集合の圏に引っぱってきて得た写像 (i.e. 線形写像であるための性質を全て満足する写像) であることからわかるように、以下の図式を可換にする。
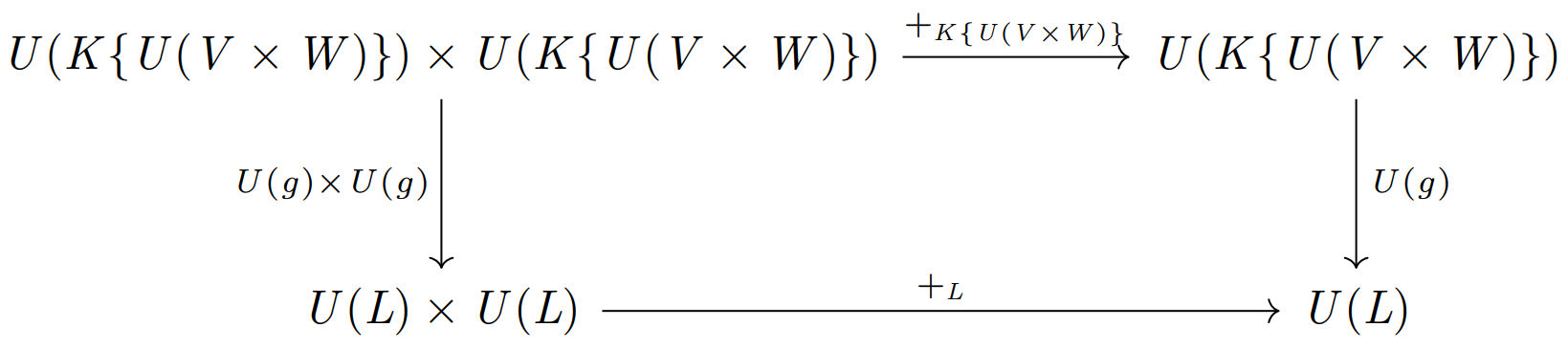
(言うまでもないことであるが、もちろん加法だけに限らずスカラー倍に関する図式など、線形写像の定義として与えられている関係式はもれなく全て満たされることになる。)
これらの事実を使って、双線形写像の定義式を変形していく。
\[
\begin{align}
f'(x,y)+_{L} f'(x',y) &= f'(x+_{V} x',y) \\
f'(x,y)+f'(x',y)&=f'(x+x',y) \\
\langle f'(x,y), f'(x',y)\rangle {\sf \, ⨟ \,} (+) &=f'(x+x',y) \\
\langle (\delta_{U(V\times W)} {\sf \, ⨟ \,} U(g))(x,y), (\delta_{U(V\times W)} {\sf \, ⨟ \,} U(g))(x',y)\rangle {\sf \, ⨟ \,} (+) &=(\delta_{U(V\times W)} {\sf \, ⨟ \,} U(g))(x+x',y) \\
\langle (\delta {\sf \, ⨟ \,} U(g))(x,y), (\delta {\sf \, ⨟ \,} U(g))(x',y)\rangle {\sf \, ⨟ \,} (+) &=(\delta {\sf \, ⨟ \,} U(g))(x+x',y) \\
\langle (U(g))(\delta(x,y)), (U(g))(\delta(x',y))\rangle {\sf \, ⨟ \,} (+) &=(U(g))(\delta(x+x',y)) \\
\langle \delta(x,y), \delta(x',y)\rangle {\sf \, ⨟ \,} (U(g) \times U(g)) {\sf \, ⨟ \,} (+) &=(U(g))(\delta(x+x',y)) \\
\langle \delta(x,y), \delta(x',y)\rangle {\sf \, ⨟ \,} ((U(g) \times U(g)) {\sf \, ⨟ \,} (+)) &=(U(g))(\delta(x+x',y)) \\
\langle \delta(x,y), \delta(x',y)\rangle {\sf \, ⨟ \,} ((+) {\sf \, ⨟ \,} U(g)) &=(U(g))(\delta(x+x',y)) \\
(\langle \delta(x,y), \delta(x',y)\rangle {\sf \, ⨟ \,} (+)) {\sf \, ⨟ \,} U(g) &=(U(g))(\delta(x+x',y)) \\
(\delta(x,y) + \delta(x',y)) {\sf \, ⨟ \,} U(g) &=(U(g))(\delta(x+x',y)) \\
(U(g))(\delta(x,y) + \delta(x',y)) &=(U(g))(\delta(x+x',y)) \\
(U(g))(\delta(x,y) + \delta(x',y)) - (U(g))(\delta(x+x',y)) &= 0_{L} \\
(U(g))(\delta(x,y) + \delta(x',y) - \delta(x+x',y)) &= 0
\end{align}
\]
同様にして他の式も変形してあげると以下の一式が得られる。
\[
\begin{align}
(U(g))(\delta(x,y) + \delta(x',y) - \delta(x+x',y)) &= 0 \\
(U(g))(\delta(x,y) + \delta(x,y') - \delta(x,y+y')) &= 0 \\
(U(g))(a\cdot\delta(x,y) - \delta(a\cdot x,y)) &= 0 \\
(U(g))(a\cdot\delta(x,y) - \delta(x,a\cdot y)) &= 0 \\
\end{align}
\]
先ほど hom 集合間の同形という形で述べたように、引き起こされる射 \(g\) とそれを引き起こす射 \(f\) との間には一対一の対応がある。 つまり、変形して得られたこちらの関係式を使って「与えられた写像が双線形写像であるのかどうか」を不備なく調べることができる。つまり以下をもう一つの同値な「双線形写像の定義」として用いることができる。
双線形写像 \(f:V,W\rightarrow L\) は線形空間の圏の射 \(g:K\{U(V\times W)\}\rightarrow L\) の内、以下の条件を満たすものとして定義できる。
任意の \(x,x':1\rightarrow U(V)\)、\(y,y':1\rightarrow U(W)\)、\(a:1\rightarrow \text{uSetOf}(K)\) に対して、以下
\[
\begin{align}
\delta(x,y) + \delta(x',y) - \delta(x+x',y) \\
\delta(x,y) + \delta(x,y') - \delta(x,y+y') \\
a\cdot\delta(x,y) - \delta(a\cdot x,y) \\
a\cdot\delta(x,y) - \delta(x,a\cdot y) \\
\end{align}
\]
の形で表せるような任意のベクトルだけからなる (有限個の) 線形結合として表されるベクトルをもれなく全て行き先の空間内のゼロベクトルへとうつす。
もっと具体的に言い換えると、双線形写像とは次の等式を満たすような写像 \(b_1,b_2,b_3,b_4\)
\[
\begin{align}
b_1(x,x',y) &= \delta(x,y) + \delta(x',y) - \delta(x+x',y) \\
b_2(x,y,y') &= \delta(x,y) + \delta(x,y') - \delta(x,y+y') \\
b_3(a,x,y) &= a\cdot\delta(x,y) - \delta(a\cdot x,y) \\
b_4(a,x,y) &= a\cdot\delta(x,y) - \delta(x,a\cdot y) \\
\end{align}
\]
について、自由線形空間の持つベクトル \(z:1\rightarrow U(K\{U(V\times W)\})\) の内
\[
z = \sum_{i=0}^n {\rm prj}_1(\xi_i)\cdot b({\rm prj}_2(\xi_i))
\]
を満たすような族 \(\xi\) と自然数 \(n\) が存在するものだけから得られる \(U(K\{U(V\times W)\})\) の部分集合がもたらす \(K\{U(V\times W)\}\) の部分線形空間 \(\langle S,i\rangle\) を核に持つ射 \(g:K\{U(V\times W)\}\rightarrow L\) (を忘却関手を介して集合の圏にうつした写像 \(U(g)\)) である。
但し、
\[
\begin{align}
B_1 &:= (U(V)\times U(V)) \times U(W) \\
B_2 &:= (U(V)\times U(W)) \times U(W) \\
B_3 &:= (\text{uSetOf}(K)\times U(V)) \times U(W) \\
B_4 &:= (\text{uSetOf}(K)\times U(V)) \times U(W) \\
b &:= [[[b_1,b_2],b_3],b_4] \\
\xi&:1\rightarrow (\text{uSetOf}(K) \times (((B_1 + B_2) + B_3) + B_4))^{\mathbb{N}} \\
n&:1\rightarrow {\mathbb{N}} \\
D &:= (\text{uSetOf}(K) \times (((B_1 + B_2) + B_3) + B_4))^{\mathbb{N}} \\
\end{align}
\]
因みに「どのようにして \(D\) の要素、つまり自然数で添え字付けた族を圏論的に構成するのか?」という部分が気になる場合は、以下の記事で具体的な構成方法を紹介しているので参考までに。
特定の条件を満たす写像が構成できることの確認
続いて、そのような構成が実際に可能であるのかを確かめていく。
現在手元にある写像 (集合の圏の射) の内、今から用いる予定の重要なものをリストアップする。
\[
\begin{align}
\delta_{U(V\times W)}&:U(V\times W) \rightarrow U(K\{U(V\times W)\}) \\
&\\
0_V&:1\rightarrow U(V) \\
(+_V)&:U(V)\times U(V) \rightarrow U(V) \\
(()^{-1}_V)&:U(V) \rightarrow U(V) \\
(\cdot_V)&:\text{uSetOf}(K)\times U(V) \rightarrow U(V) \\
&\\
0_W&:1\rightarrow U(W) \\
(+_W)&:U(W)\times U(W) \rightarrow U(W) \\
(()^{-1}_W)&:U(W) \rightarrow U(W) \\
(\cdot_W)&:\text{uSetOf}(K)\times U(W) \rightarrow U(W) \\
&\\
0_{K\{U(V\times W)\}}&:1\rightarrow U(K\{U(V\times W)\}) \\
(+_{K\{U(V\times W)\}})&:U(K\{U(V\times W)\})\times U(K\{U(V\times W)\}) \rightarrow U(K\{U(V\times W)\}) \\
(()^{-1}_{K\{U(V\times W)\}})&:U(K\{U(V\times W)\}) \rightarrow U(K\{U(V\times W)\}) \\
(\cdot_{K\{U(V\times W)\}})&:\text{uSetOf}(K)\times U(K\{U(V\times W)\}) \rightarrow U(K\{U(V\times W)\}) \\
\end{align}
\]
先ほど
\[
b_1(x,x',y) = \delta(x,y) + \delta(x',y) - \delta(x+x',y)
\]
という条件式を与えたが、この式を変形すると
\[
\begin{align}
b_1(x,x',y) &= \delta(x,y) + \delta(x',y) - \delta(x+x',y) \\
b_1(\langle \langle x,x' \rangle ,y \rangle) &= \delta(\langle x,y \rangle) +_{K\{U(V\times W)\}} \delta(\langle x',y \rangle) +_{K\{U(V\times W)\}} (()^{-1}_{K\{U(V\times W)\}})(\delta(\langle x+_V x',y \rangle)) \\
b_1(\langle \langle x,x' \rangle ,y \rangle) &= (\delta(\langle x,y \rangle) +_{K\{U(V\times W)\}} \delta(\langle x',y \rangle)) +_{K\{U(V\times W)\}} (()^{-1}_{K\{U(V\times W)\}})(\delta(\langle x+_V x',y \rangle)) \\
\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} b_1 &= (\langle x,y \rangle {\sf \, ⨟ \,} \delta +_{K\{U(V\times W)\}} \langle x',y \rangle {\sf \, ⨟ \,} \delta) +_{K\{U(V\times W)\}} ((\langle x+_V x',y \rangle {\sf \, ⨟ \,} \delta) {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}})) \\
\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} b_1 &= (\langle (\langle \langle x,y \rangle {\sf \, ⨟ \,} \delta, \langle x',y \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) ),((\langle \langle x,x' \rangle {\sf \, ⨟ \,} (+_V),y \rangle {\sf \, ⨟ \,} \delta) {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}})) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})) \\
\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} b_1 &= (\langle (\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) ),((\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_V),{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta) {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}})) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})) \\
\langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} b_1 &= \langle \langle x,x' \rangle ,y \rangle {\sf \, ⨟ \,} (\langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_V),{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})) \\
\end{align}
\]
となる。この関係式を満たしてさえいればよいので、少なくとも
\[
b_1 = \langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_V),{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})
\]
として与えれば事が済む。(加えて現在の集合論の公理に well-pointedness が含まれるので、上の条件を満たす写像の内、この \(b_1\) と異なる写像が存在しないことが保証される。)
他の \(b_2,b_3,b_4\) ついても同様に構成することができて、それらをまとめると以下のようになる。
\[
\begin{align}
b_1 &= \langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_V),{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \\
b_2 &= \langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_W) \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \\
b_3 &= \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}), \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (\cdot_V), {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \\
b_4 &= \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (\cdot_W) \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \\
\end{align}
\]
(基礎論的な問題を気にしないのであれば、この辺の議論への深入りは必要ないだろう。)
必要なベクトルだけを要素に持つ部分集合を構成するのに必要な論理式の素材が存在することの確認
今度は、構成したい部分線形空間の基底集合に該当する集合を構成するために必要な論理式が実際に組めるか (「理論の構成要素の一つ / 理論を展開していく上で使用が認められているモノの一つ」として存在しているのかどうか) を確かめる。
余談
なんでこんなことをしているのかを一応補足しておくと、集合の構成はやりたい放題できるわけではなく、例えば「インフォーマルな疑似論理式による集合の構成」というのも、(少なくとも ETCS や ZFC では) 公理的に認められている集合構成の操作の一つとして含まれていない。素朴集合論であれば、基本的になんでもやりたい放題できたが、ここでは集合を「選択公理を認めない ETCS 公理系を満たす圏の対象」としてフォーマルに扱っているため、そういった部分も慎重に行う必要性が生じてくる。
具体的に ETCS の場合は、「該当の論理式の振舞いが合成のされ方としてそのまま反映された射」が実際に圏の住人として具体的に存在していることさえ示せれば、その射に沿った部分対象分類子の引き戻しによって必要な部分対象の構成は実現する。ということでここでは愚直に「具体的に構成して確かめる」という最も手っ取り早くて納得してもらいやすいであろう手段をとることにしている。
まずインフォーマルに、必要な論理式 \(P\) は次のような条件式を満たすものである。
\[
P(z) \Leftrightarrow \exists \xi [\exists n [z = \sum_{i=0}^n {\rm prj}_1(\xi_i)\cdot b({\rm prj}_2(\xi_i))]]
\]
とはいえ、総和の記号は単なる便宜的な表記であり、これだけの情報では部分集合を構成するのに用いるフォーマルな式として使用できるかが不明瞭である。
ということで、それを愚直に確かめる。
\[
\begin{align}
P(z) &\Leftrightarrow \exists \xi [\exists n [z = \sum_{i=0}^n {\rm prj}_1(\xi_i)\cdot b({\rm prj}_2(\xi_i))]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \sum_{i=0}^n {\rm prj}_1(\xi_i)\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\xi_i))]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == n {\sf \, ⨟ \,} {\rm rec}_{{\mathbb{N}}}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, {\rm elToArr}(\lambda \langle i, t \rangle . (\langle i {\sf \, ⨟ \,} {\rm succ}, t +_{K\{U(V\times W)\}} ({\rm prj}_1(\xi_i)\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\xi_i))) \rangle)) ) {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == n {\sf \, ⨟ \,} {\rm rec}_{{\mathbb{N}}}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, {\rm elToArr}(\lambda \langle i, t \rangle . (\langle i {\sf \, ⨟ \,} {\rm succ}, t +_{K\{U(V\times W)\}} ({\rm prj}_1(\langle \xi, i \rangle {\sf \, ⨟ \,} {\rm ev})\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\langle \xi, i \rangle {\sf \, ⨟ \,} {\rm ev}))) \rangle))) {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == n {\sf \, ⨟ \,} {\rm rec}_{{\mathbb{N}}}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, {\rm elToArr}(\lambda \alpha . (\langle (\alpha {\sf \, ⨟ \,} {\rm prj}_1) {\sf \, ⨟ \,} {\rm succ}, (\alpha {\sf \, ⨟ \,} {\rm prj}_2) +_{K\{U(V\times W)\}} ({\rm prj}_1(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}))) \rangle))) {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \lambda \alpha . (\langle \alpha {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, (\alpha {\sf \, ⨟ \,} {\rm prj}_2) +_{K\{U(V\times W)\}} ({\rm prj}_1(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}))) \rangle)\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \lambda \alpha . (\langle \alpha {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle \alpha {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_1(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle)\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \lambda \alpha . (\langle \alpha {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle \alpha {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_1(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})\cdot_{K\{U(V\times W)\}} b({\rm prj}_2(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle)\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \lambda \alpha . (\langle \alpha {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle \alpha {\sf \, ⨟ \,} {\rm prj}_2, \langle (\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_1, ({\rm prj}_2(\langle \xi, \alpha {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev})) {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle)\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \lambda \alpha . ( \langle \xi, \alpha \rangle {\sf \, ⨟ \,} (\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle (\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_1, ((\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle))\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle (\langle \langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle, \xi {\sf \, ⨟ \,} \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle (\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_1, ((\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle \xi {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle (\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_1, ((\langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev}) {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [z == \langle \xi {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [\langle z, (\langle \xi {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , n \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})})]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\exists n:{\mathbb{N}} [\langle \langle z,\xi \rangle, n \rangle {\sf \, ⨟ \,} (\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, (\langle ({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , {\rm prj}_2 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})}))]] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow \exists \xi:D [\langle z,\xi \rangle {\sf \, ⨟ \,} \lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, (\langle ({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , {\rm prj}_2 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})})] {\sf \, ⨟ \,} (\exists_{{\mathbb{N}}})] \\
z {\sf \, ⨟ \,} P &\Leftrightarrow z {\sf \, ⨟ \,} \lambda[\lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, (\langle ({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} b \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , {\rm prj}_2 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})})] {\sf \, ⨟ \,} (\exists_{{\mathbb{N}}})] {\sf \, ⨟ \,} (\exists_{D}) \\
\end{align}
\]
よって次のような形で、部分集合を構成するために必要になる論理式の原料が得られる。
\[
\begin{align}
P &= \lambda[\lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, (\langle ({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} [[[b_1,b_2],b_3],b_4] \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , {\rm prj}_2 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})})] {\sf \, ⨟ \,} (\exists_{{\mathbb{N}}})] {\sf \, ⨟ \,} (\exists_{D}) \\
&= \lambda[\lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, (\langle ({\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2) {\sf \, ⨟ \,} (\langle {\rm const}(\langle {\rm zero}, 0_{K\{U(V\times W)\}} \rangle), \lambda[\langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 {\sf \, ⨟ \,} {\rm succ}, \langle {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} \langle {\rm prj}_1, {\rm prj}_2 {\sf \, ⨟ \,} [[[\langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_V),{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}),\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1,{\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (+_W) \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})],\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}), \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} (\cdot_V), {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})],\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \delta \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (\cdot_W) \rangle {\sf \, ⨟ \,} \delta {\sf \, ⨟ \,} (()^{-1}_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}})] \rangle {\sf \, ⨟ \,} (\cdot_{K\{U(V\times W)\}}) \rangle {\sf \, ⨟ \,} (+_{K\{U(V\times W)\}}) \rangle]\rangle {\sf \, ⨟ \,} {\rm iterate}) , {\rm prj}_2 \rangle {\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} {\rm prj}_2) \rangle {\sf \, ⨟ \,} (==_{U(K\{V\times W\})})] {\sf \, ⨟ \,} (\exists_{{\mathbb{N}}})] {\sf \, ⨟ \,} (\exists_{D}) \\
\end{align}
\]
ここで、
- \({\rm iterate}\) の構成は「自然数対象を持つトポスで有名な巨大数である「グラハム数」を構成してみる」
- \((\exists_{D})\) を始めとする論理演算子の構成は「置換公理型を認めない初等トポスの一般論の中で、集合 {x∈X|P(x)} はどのようにして構成されるのか」
を参照。
(ターゲットとなる論理式が部分集合の構成に本当に使用できるものの一つであるのかを明確化する目的で論理式の素材となる射の具体的な構成を与えているが、流石にこの射を直接議論に用いることはしない。)
\(P\) の存在が確かめられたので、あとは引き戻しによって欲しかった部分集合 \(\langle R,P^{-1}({\rm true}) \rangle\) が導かれる。
構成した部分集合に加法・スカラー倍を誘導する
\(\langle R,P^{-1}({\rm true}) \rangle\) は現段階では単なる \(U(K\{U(V\times W)\})\) の部分集合であるが、線形空間 \(K\{U(V\times W)\}\) の持つ構造をその部分集合に誘導することで、一つの \(K\{U(V\times W)\}\) の部分線形空間が得られる。このことをこの節で議論していく。
まずは加法の構造を誘導する。
次の図式
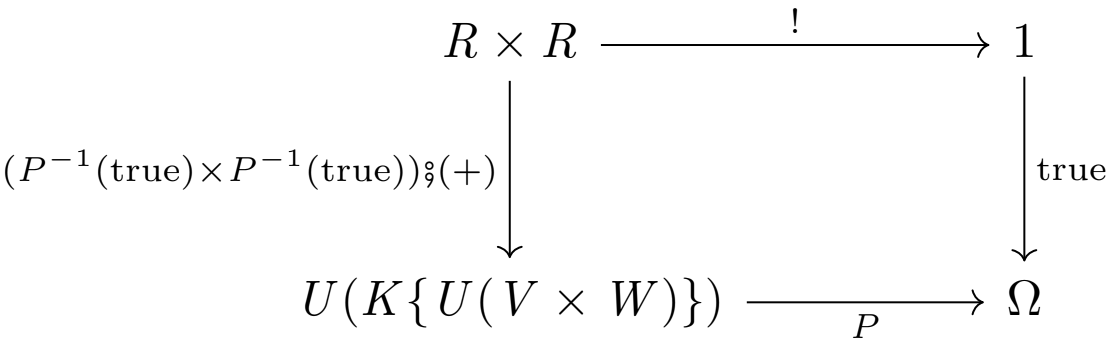
が可換であれば、引き戻しの普遍性より、以下の図式を可換にする一意的な射 \(h:R\times R \rightarrow R\) が引き起こされる。
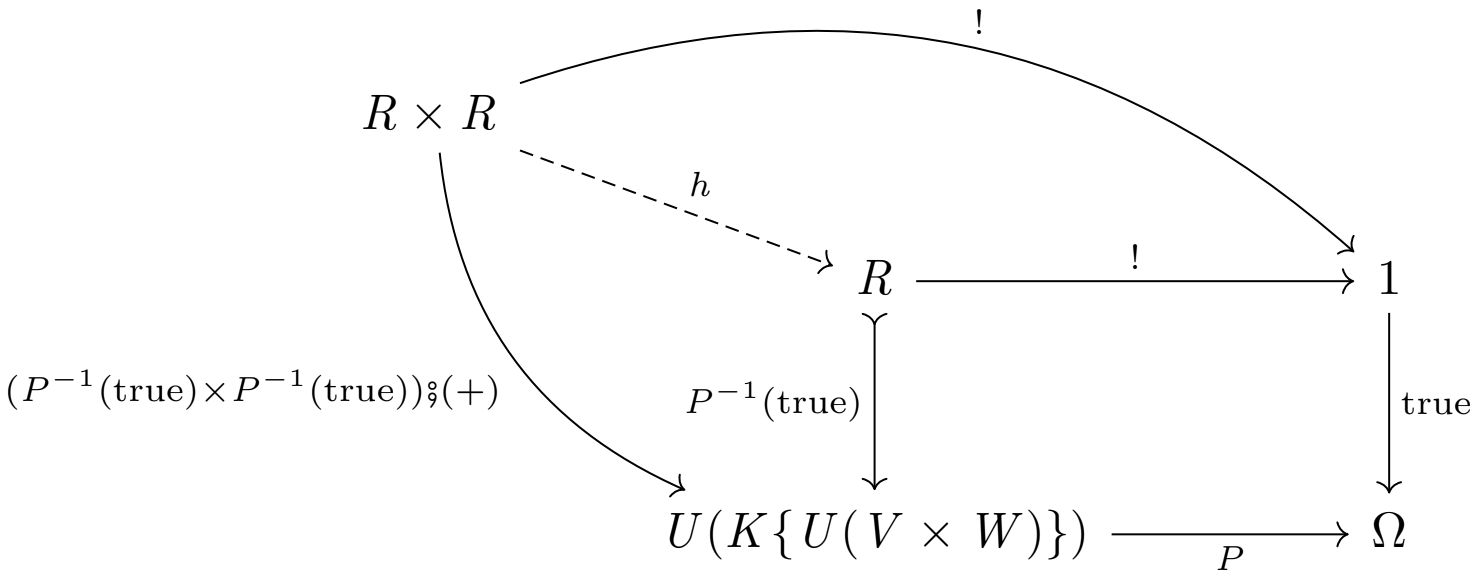
図式を使わずに言い換えると、
\[
(((P^{-1}({\rm true}))\times (P^{-1}({\rm true}))) {\sf \, ⨟ \,} (+)) {\sf \, ⨟ \,} P = ! {\sf \, ⨟ \,} {\rm true}
\]
が満たされれば、
\[
h {\sf \, ⨟ \,} (P^{-1}({\rm true})) = (((P^{-1}({\rm true}))\times (P^{-1}({\rm true}))) {\sf \, ⨟ \,} (+))
\]
を成立させるような一意的な射 \(h\) の存在が従うということである。
問題はその正方図式が本当に可換であるのかという点だが、これについては以下のようにして簡単に確認することができる。(理論的には愚直な式変形によって証明することもできるとは思うが、その式を弄ることに気が進まないので、これに関してはシンプルでわかりやすい方法に逃げさせていただく。)
第一に射 \(P\) の定義式のカオスさに狼狽えてしまいそうになるが、結局重要なのは「与えられたベクトルが、特定のフォーマットの (無限通りの) ベクトルの内、それらの中から選び出された有限個のベクトルの線形結合の形として表すことができるかの判定式を提供する単なる道具」でしかないということである。
この点を踏まえると、引き戻しの定義より、射 \(P^{-1}({\rm true})\) を通して行きつく \(U(K\{U(V\times W)\})\) の任意の要素 (ベクトル) は、その条件を満たしているベクトルということになるので、
\[
(((P^{-1}({\rm true}))\times (P^{-1}({\rm true}))) {\sf \, ⨟ \,} (+)) {\sf \, ⨟ \,} P = ! {\sf \, ⨟ \,} {\rm true}
\]
は、単に
- 「その条件を満たすベクトル同士の和も再びその条件を満たすこと」が如何なる組み合わせに対しても成立するのか
を問うているだけである。これを確認するのは難しくない。
まず \(z_1,z_2:1\rightarrow R\) を集合 \(R\) の要素とする。
「\(R\) の要素である」以上、「\(R\) の要素であるための族と自然数」が存在していなければならず、それらを以下のように名付ける。
- \(\langle \alpha,n_1 \rangle\): \(z_1\) が \(R\) の要素であることを保証する族と自然数
- \(\langle \beta,n_2 \rangle\): \(z_2\) が \(R\) の要素であることを保証する族と自然数
ここで、
\[
c_n =
\begin{cases}
\alpha_n & \text{ if } 0\le n \le n_1 \\
\beta_{n-(n_1 + 1)} & \text{ if } n_1 + 1 \le n \le n_1 + 1 + n_2 \\
\langle 0, \langle \langle 0, 0_V \rangle, 0_W \rangle {\sf \, ⨟ \,} {\rm inj}_2 \rangle & \text{ otherwise }
\end{cases}
\]
といった感じの条件を満たす族 \(c\) を与えることができれば (その族の存在は自分で確かめてほしい。また otherwise の部分は任意なので、上の通りである必要はない。引き算の構成法は、この記事を参照。)
\[
\begin{align}
z_1 + z_2 &= \left(\sum_{i=0}^{n_1} {\rm prj}_1(\alpha_i)\cdot b({\rm prj}_2(\alpha_i))\right) + \left(\sum_{i=0}^{n_2} {\rm prj}_1(\beta_i)\cdot b({\rm prj}_2(\beta_i))\right) \\
&= \left(\sum_{i=0}^{n_1} {\rm prj}_1(\alpha_i)\cdot b({\rm prj}_2(\alpha_i))\right) + \left(\sum_{i=n_1 + 1}^{(n_1 + 1) + n_2} {\rm prj}_1(\beta_{i - (n_1 + 1)})\cdot b({\rm prj}_2(\beta_{i - (n_1 + 1)}))\right) \\
&= \left(\sum_{i=0}^{n_1} {\rm prj}_1(c_i)\cdot b({\rm prj}_2(c_i))\right) + \left(\sum_{i=n_1 + 1}^{(n_1 + 1) + n_2} {\rm prj}_1(c_i)\cdot b({\rm prj}_2(c_i))\right) \\
&= \sum_{i=0}^{(n_1 + 1) + n_2} {\rm prj}_1(c_i)\cdot b({\rm prj}_2(c_i)) \\
\end{align}
\]
より、\(z_1 + z_2\) は「特定のフォーマットの (無限通りの) ベクトルの内、それらの中から選び出された有限個のベクトルの線形結合の形として表すことができる」という条件を満たす。
ということで、その正方図式が実際に可換図式であったということになり、射 \(h:R\times R \rightarrow R\) を引き起こす事の確認が取れた。
その引き起こされる射を \((+_{S})\) と名付けると、その射のそもそもの定義から
\[
(+_{S}) {\sf \, ⨟ \,} (P^{-1}({\rm true})) = ((P^{-1}({\rm true}))\times (P^{-1}({\rm true}))) {\sf \, ⨟ \,} (+_{U(K\{U(V\times W)\})})
\]
が満たされるわけだが、このことは後々 \((P^{-1}({\rm true})))\) が線形性を満たすことの確認に必要になる。
また同様の手順を踏むことで、加法に限らずスカラー倍や加法の逆元参照演算等を誘導する事もできて、それらの写像と共に集合 \(R\) の上に一つの線形空間の構造 \(S := \langle R,... \rangle\) が組みあがる。
そしてさらに集合の圏のモニック射 \(P^{-1}({\rm true})\) は、線形空間の圏のモニック射 \(i:S\rightarrow K\{U(V\times W)\}\) を定め、線形空間 \(S\) と共に \(K\{U(V\times W)\}\) の部分線形空間 \(\langle S,i \rangle\) の構造を導く。
テンソル積の普遍性が線形空間の圏の中でのコイコライザとして見做せることを確認する
ここで一旦現状を整理する。
まず先ほど何故ヘンテコな部分線形空間 \(\langle S,i \rangle\) を構成したのかといえば、
- 線形写像 \(g:K\{U(V\times W)\}\rightarrow L\) について、その線形写像がその部分線形空間内の全てのベクトルを、コドメインとして設定されている空間 \(L\) のゼロベクトルへと漏れなくうつすようなものであれば、その線形写像 \(g\) と対応する写像 \(U(V\times W)\rightarrow U(L)\) は、\(V,W,L\) が持つ演算構造に関して双線形写像となる
という話があったことによる。
つまり、線形空間の圏の射 \(g:K\{U(V\times W)\}\rightarrow L\) は、部分線形空間の構成要素であるモニック射 \(i\) を前方から合成して得られる射 (つまりドメインをその部分空間へと制限してあげたもの) がゼロ射となれば、それは双線形写像と関係のあるものとして捉えることができる。
簡単にまとめると、
- 双線形写像であること ⇔ その部分空間を定めるモニック射を前方から合成して得られる射 (その部分空間への制限として得られる射) がゼロ射
となるが、これはつまり
- 双線形写像であること ⇔ そのモニック射とゼロ射からなる2つの平行な射をコイコライズできる
ということである。
ここまで分かれば、どのようにしてテンソル積を構成するのかは見えてくるだろう。そもそもの定義が、
- 双線形写像であるなら、テンソル積への普遍双線形写像とテンソル積からの仲介射の合成に分解できる
であったわけだが、これが
- そのモニック射とゼロ射からなる2つの平行な射をコイコライズできるなら、テンソル積への普遍射とテンソル積からの仲介射の合成に分解できる
と言い換えられるようになったのである。この説明からもう明らかであると思うがこれはテンソル積が
- \(i\) と \(0\) のコイコライザの普遍射を付随する余極限対象であること
を云っているほかない。
そして線形空間の圏が「有限余完備かつ点付き (ゼロ対象を持つ) である」ということを事実として認めてしまえば、この時点でテンソル積の構成が線形空間の圏で実現可能であることが明らかになったことになる。
モニック射とゼロ射とのコイコライザは、部分線形空間を潰して得られる商線形空間といった意味合いになるので、つまり \(V,W\) のテンソル積 \(V\otimes W\) とは商線形空間 \(K\{U(V\times W)\} / \langle S,i \rangle\) として与えることができる。
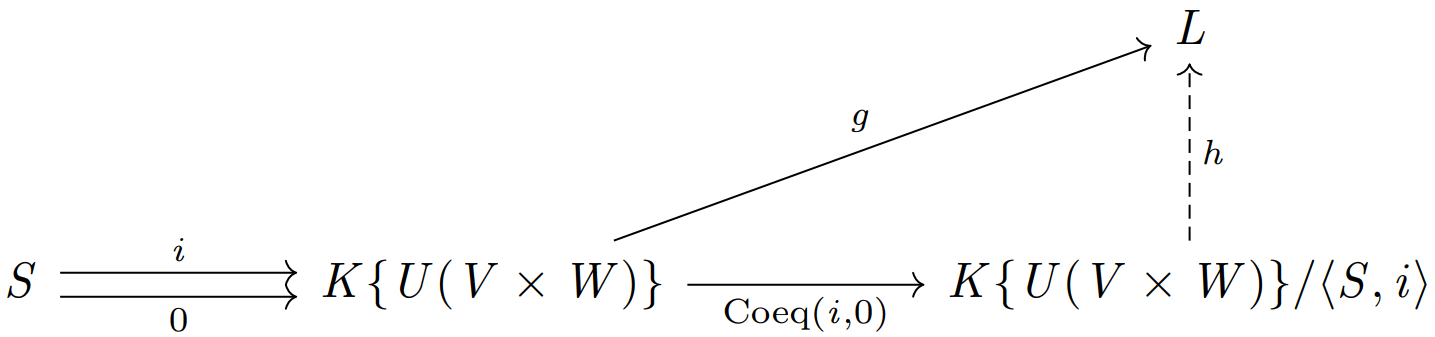
余談
先ほど基底集合から出発し、その基底集合に線形空間の構造を誘導することで部分線形空間を得たが、この商線形空間の構成は「線形空間の圏の中で完結している」という点に気を付けてほしい。
つまりそうして得られる余極限対象は集合ではなく "線形空間" であり、その対象は既に加法やスカラー倍といった特定の線形空間の構造を全て持ち合わせている。
集合の圏に普遍射を持っていく
前節でテンソル積の構成は済んでいるのだが、コイコライザとして得られる普遍射と対応する写像は自由線形空間の基底集合からの写像というフォーマットとなっていて、そのままだと少し扱いにくい。
そこで最後の仕上げとして、より扱いやすい形に変形していく。
とはいってもやることは単純で、自由対象の普遍性の図式を見れば一目でわかるが、
- 普遍射を忘却関手を使って集合の圏に持っていって得られる写像の前方から \(\delta_{U(V\times W)}\) を合成してあげるだけ
である。
\[
\otimes := \delta_{U(V\times W)} {\sf \, ⨟ \,} U({\rm Coeq}(i,0))
\]
余談
一般的抽象的ナンセンスより、\({\rm Coeq}(i,0)\) は (線形空間の圏で) エピックであるが、だからといってその射と対応する写像である \(\otimes: U(V\times W)\rightarrow U(V\otimes W)\) までもが (集合の圏で) エピックとなることは従わない。
実際 \(\otimes\) は全射ではない。
圏論的な構成方法
Chris Grossack 様により書かれた僕が説明するまでもないと思えるような素晴らしい記事があったので、そのページへのリンクを以下に勝手に貼らせていただく。
タグ一覧:

