雑記帳
通常の水素の方程式を2粒子系に対するシュレーディンガー方程式を出発点に導出する。
(書きかけ)
前書き
このページで説明を行うのは、水素の方程式というスタートラインに立つまでの道のりであり、方程式を実際に解く部分については次回行う。
また圏論的な見方を積極的に活用するというこのサイトの方針に伴い、変数ではなく写像そのものを重要視するということを意識して議論を進めていく。
これによって例えば、「写像」と「写像の取る値」をくどいほど明確に区別したり、「どの変数で微分するのか」ではなく「何番目の入力について微分をするのか」というようにして微分を考えたりなどしていくが、それらはそういった理由により意図して行われているものであるということを留意しておいてほしい。
水素原子を解析する方程式に辿り着くまで...

出発点となる大本の方程式 (2粒子系に対するシュレーディンガー方程式)
\[
i\hbar \frac{\partial C_{\psi}}{\partial t}(\boldsymbol{r}_1,\boldsymbol{r}_2, t) = -\frac{\hbar^2}{2M}(\nabla_1^2 C_{\psi})(\boldsymbol{r}_1,\boldsymbol{r}_2, t) -\frac{\hbar^2}{2m}(\nabla_2^2 C_{\psi})(\boldsymbol{r}_1,\boldsymbol{r}_2, t) - \frac{1}{4\pi\varepsilon_0}\frac{e^2}{\| \boldsymbol{r}_1 - \boldsymbol{r}_2 \|}\cdot C_{\psi}(\boldsymbol{r}_1,\boldsymbol{r}_2, t) \\
\]
(..)
定常状態を求める方程式に書き換える
「シュレーディンガー方程式から与えられた系での定常状態を求める方程式を誘導する。」で説明した通り、上で与えたシュレーディンガー方程式で状態発展を追いかけることができる系の定常状態を求める方程式は、
\[
\begin{align}
C_{\psi}(\boldsymbol{r}_1,\boldsymbol{r}_2,t) &= e^{\frac{E}{i\hbar}t} \cdot C_a(\boldsymbol{r}_1,\boldsymbol{r}_2) \\
E \cdot C_a(\boldsymbol{r}_1,\boldsymbol{r}_2) &= -\frac{\hbar^2}{2M}(\nabla_1^2 C_a)(\boldsymbol{r}_1,\boldsymbol{r}_2) -\frac{\hbar^2}{2m}(\nabla_2^2 C_a)(\boldsymbol{r}_1,\boldsymbol{r}_2) - \frac{1}{4\pi\varepsilon_0}\frac{e^2}{\| \boldsymbol{r}_1 - \boldsymbol{r}_2 \|}\cdot C_a(\boldsymbol{r}_1,\boldsymbol{r}_2) \\
\end{align}
\]
(..)
原子核の位置を基点とする電子の相対位置に対して振幅を定める関数についての方程式に書き換える
\[
\begin{align}
\eta(\boldsymbol{d}) &= (C_a \circ j_r)(\boldsymbol{r}_1,\boldsymbol{d}) \\
E\eta(\boldsymbol{d}) &= -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(\boldsymbol{d}) - \frac{e^2}{4\pi \varepsilon_0 \| \boldsymbol{d} \|}\eta(\boldsymbol{d}) \\
\end{align}
\]
(..)
球面の式を通して間接的に位置を指定できるようにした関数に対する方程式に書き換える
球面の式が合成された写像の微分が満たす関係式を求める
任意の基準点を \(\boldsymbol{r}_0\) とし、球面の式を通して空間内の一点を \(\boldsymbol{r}_0\) からの距離と方向を意味する入力から指定する関数を \(j:{\mathbb{R}}^3\rightarrow{\mathbb{R}}^3\) とする。
具体的には、\(j\) は
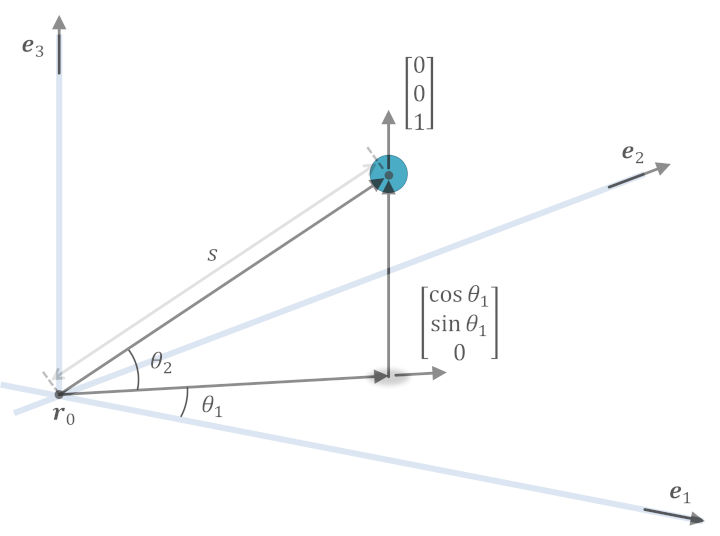
- \(s\): 基準点からの距離
- \(\theta_1\): 基準点から目標位置までの変位ベクトルの \(\boldsymbol{e}_1, \boldsymbol{e}_2\) が張る平面上への射影ベクトルと \(\boldsymbol{e}_1\) とのなす角
- \(\theta_2\): 基準点から目標位置までの変位ベクトルの \(\boldsymbol{e}_1, \boldsymbol{e}_2\) が張る平面上への射影ベクトルとその大本の変位ベクトルとのなす角
としたとき、以下の関係式を満たす写像である。
\[
j(s,\theta_1, \theta_2) = \boldsymbol{r}_0 + s\left\{
\cos \theta_2
\left[
\begin{matrix}
\cos \theta_1 \cr
\sin \theta_1 \cr
0
\end{matrix}
\right]
+
\sin \theta_2
\left[
\begin{matrix}
0 \cr
0 \cr
1
\end{matrix}
\right]
\right\}
\]
余談
位置ベクトルを「原点と指定位置を結ぶ矢印」として見たときの、その極座標表示を考えているというよりかは、「3つのパラメータを用いて位置を間接的に指定する」という見方をとっている。
また極座標表示を考える場合、\(\theta_2\) を「z-軸とのなす角」として与えることが多いが、これについては後から合わせることができるため問題視する必要は無い。
ここで、「基準点からの距離」と「基準点からの方向」に分解して水素の方程式を考察できるようにするために、前節で求めた \(\eta\) に関する方程式を
\[
\varphi = \eta \circ j
\]
で定まる \(\varphi\) に関する方程式に書き換えていく。
まず \(j\) が合成された任意の関数 \(f\) の微分
\[
\partial_i (f \circ j)
\]
がどういった形になるのかを、全ての \(i\) について調べると以下のようになる。
\[
\begin{align}
(\partial_1 (f \circ j))(s,\theta_1, \theta_2) &=
\left[
\begin{matrix}
\cos \theta_1 \cos \theta_2 \cr
\sin \theta_1 \cos \theta_2 \cr
\sin \theta_2
\end{matrix}
\right] \cdot
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] \\
(\partial_2 (f \circ j))(s,\theta_1, \theta_2) &=
s\left[
\begin{matrix}
-\sin \theta_1 \cos \theta_2 \cr
\cos \theta_1 \cos \theta_2 \cr
0
\end{matrix}
\right] \cdot
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] \\
(\partial_3 (f \circ j))(s,\theta_1, \theta_2) &=
s\left[
\begin{matrix}
-\cos \theta_1 \sin \theta_2 \cr
-\sin \theta_1 \sin \theta_2 \cr
\cos \theta_2
\end{matrix}
\right] \cdot
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] \\
\end{align}
\]
行列を使ってこれらの関係式を一本の式に纏めると
\[
\left[
\begin{matrix}
(\partial_1 (f \circ j))(s,\theta_1, \theta_2) \cr
(\partial_2 (f \circ j))(s,\theta_1, \theta_2) \cr
(\partial_3 (f \circ j))(s,\theta_1, \theta_2)
\end{matrix}
\right] =
\left[
\begin{matrix}
\cos \theta_1 \cos \theta_2 & \sin \theta_1 \cos \theta_2 & \sin \theta_2 \cr
-s\sin \theta_1 \cos \theta_2 & s\cos \theta_1 \cos \theta_2 & 0 \cr
-s\cos \theta_1 \sin \theta_2 & -s\sin \theta_1 \sin \theta_2 & s\cos \theta_2
\end{matrix}
\right]
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right]
\]
が得られる。
見やすいように、
\[
\begin{align}
A(s,\theta_1, \theta_2) &=
\left[
\begin{matrix}
\cos \theta_1 \cos \theta_2 & \sin \theta_1 \cos \theta_2 & \sin \theta_2 \cr
-s\sin \theta_1 \cos \theta_2 & s\cos \theta_1 \cos \theta_2 & 0 \cr
-s\cos \theta_1 \sin \theta_2 & -s\sin \theta_1 \sin \theta_2 & s\cos \theta_2
\end{matrix}
\right] \\
\boldsymbol{b}_f(s,\theta_1, \theta_2) &= \sum_{k}\left( (\partial_k(f\circ j))(s,\theta_1, \theta_2) \boldsymbol{e}_k \right) \\
B(s,\theta_1, \theta_2) &= (A(s,\theta_1, \theta_2))^{-1} \\
&=
\left[
\begin{matrix}
\cos \theta_1 \cos \theta_2 & -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} & -\frac{1}{s} \cos \theta_1 \sin \theta_2 \cr
\sin \theta_1 \cos \theta_2 & \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} & -\frac{1}{s} \sin \theta_1 \sin \theta_2 \cr
\sin \theta_2 & 0 & \frac{1}{s} \cos \theta_2
\end{matrix}
\right]
\end{align}
\]
と置くと、
\[
\begin{align}
\boldsymbol{b}_f(s,\theta_1, \theta_2) &=
A(s,\theta_1, \theta_2)
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] \\
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] &=
(A(s,\theta_1, \theta_2))^{-1} \boldsymbol{b}_f(s,\theta_1, \theta_2) \\
\left[
\begin{matrix}
((\partial_1 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_2 f) \circ j)(s,\theta_1, \theta_2) \cr
((\partial_3 f) \circ j)(s,\theta_1, \theta_2)
\end{matrix}
\right] &= B(s,\theta_1, \theta_2) \boldsymbol{b}_f(s,\theta_1, \theta_2) \\
((\partial_i f) \circ j)(s,\theta_1, \theta_2) &= \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) \boldsymbol{b}_f(s,\theta_1, \theta_2)) \\
(\partial_i f) \circ j &= \lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) \boldsymbol{b}_f(s,\theta_1, \theta_2)) \right\} \\
\end{align}
\]
という関係式が得られる。
得られた関係式を方程式に適用する
先ほど得られた関係式
\[
(\partial_i f) \circ j = \lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) \boldsymbol{b}_f(s,\theta_1, \theta_2)) \right\}
\]
を \(\eta\) に関する方程式に適用していく。
\[
\begin{align}
E\eta(\boldsymbol{d}) &= -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(\boldsymbol{d}) - \frac{e^2}{4\pi \varepsilon_0 \| \boldsymbol{d} \|}\eta(\boldsymbol{d}) \\
\lambda \boldsymbol{d}.\left\{ E\eta(\boldsymbol{d}) \right\} &= \lambda \boldsymbol{d}.\left\{ -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(\boldsymbol{d}) - \frac{e^2}{4\pi \varepsilon_0 \| \boldsymbol{d} \|}\eta(\boldsymbol{d}) \right\} \\
\lambda \boldsymbol{d}.\left\{ E\eta(\boldsymbol{d}) \right\} \circ j &= \lambda \boldsymbol{d}.\left\{ -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(\boldsymbol{d}) - \frac{e^2}{4\pi \varepsilon_0 \| \boldsymbol{d} \|}\eta(\boldsymbol{d}) \right\} \circ j \\
\left( \lambda \boldsymbol{d}.\left\{ E\eta(\boldsymbol{d}) \right\} \circ j \right)(s,\theta_1, \theta_2) &= \left( \lambda \boldsymbol{d}.\left\{ -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(\boldsymbol{d}) - \frac{e^2}{4\pi \varepsilon_0 \| \boldsymbol{d} \|}\eta(\boldsymbol{d}) \right\} \circ j \right)(s,\theta_1, \theta_2) \\
E\eta(j(s,\theta_1, \theta_2)) &= -\frac{\hbar^2}{2\mu} (\nabla^2 \eta)(j(s,\theta_1, \theta_2)) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\eta(j(s,\theta_1, \theta_2)) \\
E\cdot(\eta\circ j)(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} ((\nabla^2 \eta)\circ j)(s,\theta_1, \theta_2) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}(\eta\circ j)(s,\theta_1, \theta_2) \\
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} ((\nabla^2 \eta)\circ j)(s,\theta_1, \theta_2) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\varphi(s,\theta_1, \theta_2) \\
\end{align}
\]
ここで、
\[
\begin{align}
(\nabla^2 \eta)\circ j &= (\sum_i (\partial_i^2 \eta))\circ j \\
&= \sum_i ((\partial_i^2 \eta)\circ j) \\
&= \sum_i ((\partial_i(\partial_i\eta))\circ j) \\
\end{align}
\]
\(f=\partial_i\eta\) として、先ほどの関係式を適用すると
\[
\begin{align}
& \sum_i ((\partial_i(\partial_i\eta))\circ j) \\
=& \sum_i (\lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) \boldsymbol{b}_{\partial_i\eta}(s,\theta_1, \theta_2)) \right\}) \\
=& \sum_i \left(\lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) (\sum_{k}\left( (\partial_k((\partial_i\eta)\circ j))(s,\theta_1, \theta_2) \boldsymbol{e}_k \right))) \right\}\right) \\
\end{align}
\]
\((\partial_i\eta)\circ j\) にも同じ関係式が適用できて
\[
\begin{align}
& \sum_i \left(\lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) (\sum_{k}\left( (\partial_k((\partial_i\eta)\circ j))(s,\theta_1, \theta_2) \boldsymbol{e}_k \right))) \right\}\right) \\
=& \sum_i \left(\lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) (\sum_{k}\left( (\partial_k(\lambda \langle s',\theta_1', \theta_2' \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s',\theta_1', \theta_2') \boldsymbol{b}_\eta(s',\theta_1', \theta_2')) \right\}))(s,\theta_1, \theta_2) \boldsymbol{e}_k \right))) \right\}\right) \\
=& \sum_i \left(\lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \boldsymbol{e}_i\cdot(B(s,\theta_1, \theta_2) (\sum_{k}\left( (\lambda \langle s',\theta_1', \theta_2' \rangle.\left\{ \boldsymbol{e}_i\cdot((\partial_k B)(s',\theta_1', \theta_2') \boldsymbol{b}_\eta(s',\theta_1', \theta_2') + B(s',\theta_1', \theta_2') (\partial_k \boldsymbol{b}_\eta)(s',\theta_1', \theta_2')) \right\})(s,\theta_1, \theta_2) \boldsymbol{e}_k \right))) \right\}\right) \\
\end{align}
\]
これを整理すると
\[
\begin{align}
((\nabla^2 \eta)\circ j)(s,\theta_1, \theta_2) =& \sum_l \left\{ (\partial_l \varphi)(s,\theta_1, \theta_2) \left\{ \sum_{i,k} \left\{
\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_k \} \}
\{ \boldsymbol{e}_i\cdot \{ (\partial_k B)(s,\theta_1, \theta_2) \boldsymbol{e}_l \} \}
\right\} \right\} \right\} \\
& + \sum_l \left\{ (\partial_l^2 \varphi)(s,\theta_1, \theta_2) \left\{ \sum_{i} \left\{
\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_l \} \}^2
\right\} \right\} \right\} \\
& + 2\sum_{\substack{k,l \\ k < l }} \left\{ (\partial_k \partial_l \varphi)(s,\theta_1, \theta_2) \left\{ \sum_{i} \left\{
\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_k \} \}
\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_l \} \}
\right\} \right\} \right\} \\
\end{align}
\]
続いて各項を地道に計算していく。
■ \((\partial_1 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i,k} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_k \} \} \{ \boldsymbol{e}_i\cdot \{ (\partial_k B)(s,\theta_1, \theta_2) \boldsymbol{e}_1 \} \}
\right\} \\
=\:& \cos \theta_1 \cos \theta_2 \cdot 0 +\left( -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} \right)\cdot \left( -\sin \theta_1 \cos \theta_2 \right) +\left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right)\cdot \left( -\cos \theta_1 \sin \theta_2 \right) \\
&+ \sin \theta_1 \cos \theta_2 \cdot 0 +\left( \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right)\cdot \left( \cos \theta_1 \cos \theta_2 \right) +\left( -\frac{1}{s} \sin \theta_1 \sin \theta_2 \right)\cdot \left( -\sin \theta_1 \sin \theta_2 \right) \\
&+ \sin \theta_2 \cdot 0 + 0\cdot 0 +\left( \frac{1}{s} \cos \theta_2 \right)\cdot \cos \theta_2 \\
=\:& \frac{1}{s}(1+\sin^2 \theta_2 + \cos^2 \theta_2) \\
=\:& \frac{2}{s} \\
\end{align}
\]
■ \((\partial_2 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i,k} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_k \} \} \{ \boldsymbol{e}_i\cdot \{ (\partial_k B)(s,\theta_1, \theta_2) \boldsymbol{e}_2 \} \}
\right\} \\
=\:& \cos \theta_1 \cos \theta_2 \cdot \left( -\frac{1}{s^2} \frac{\sin \theta_1}{\cos \theta_2} \right) +\left( -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} \right)\cdot \left( -\frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right) +\left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right)\cdot \left( -\frac{1}{s} \frac{\sin \theta_1 \sin \theta_2}{\cos^2 \theta_2} \right) \\
&+ \sin \theta_1 \cos \theta_2 \cdot \left( \frac{1}{s^2} \frac{\cos \theta_1}{\cos \theta_2} \right) +\left( \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right)\cdot \left( \frac{1}{s} \frac{-\sin \theta_1}{\cos \theta_2} \right) +\left( -\frac{1}{s} \sin \theta_1 \sin \theta_2 \right)\cdot \left( \frac{1}{s} \frac{\cos \theta_1 \sin \theta_2}{\cos^2 \theta_2} \right) \\
=\:& 0 \\
\end{align}
\]
■ \((\partial_3 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i,k} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_k \} \} \{ \boldsymbol{e}_i\cdot \{ (\partial_k B)(s,\theta_1, \theta_2) \boldsymbol{e}_3 \} \}
\right\} \\
=\:& \cos \theta_1 \cos \theta_2 \cdot \left( \frac{1}{s^2} \cos \theta_1 \sin \theta_2 \right) +\left( -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} \right)\cdot \left( \frac{1}{s} \sin \theta_1 \sin \theta_2 \right) +\left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right)\cdot \left( -\frac{1}{s} \cos \theta_1 \cos \theta_2 \right) \\
&+ \sin \theta_1 \cos \theta_2 \cdot \left( \frac{1}{s^2} \sin \theta_1 \sin \theta_2 \right) +\left( \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right)\cdot \left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right) +\left( -\frac{1}{s} \sin \theta_1 \sin \theta_2 \right)\cdot \left( -\frac{1}{s} \sin \theta_1 \cos \theta_2 \right) \\
&+ \sin \theta_2 \cdot \left( -\frac{1}{s^2} \cos \theta_2 \right) + 0 +\left( \frac{1}{s} \cos \theta_2 \right)\cdot \left( -\frac{1}{s} \sin \theta_2 \right) \\
=\:& \frac{1}{s^2}(\cos \theta_2 \sin \theta_2 - \frac{\sin \theta_2}{\cos \theta_2} + \cos \theta_2 \sin \theta_2 - 2 \cos \theta_2 \sin \theta_2) \\
=\:& -\frac{2}{s^2}\frac{\sin \theta_2}{\cos \theta_2} \\
\end{align}
\]
■ \((\partial_1^2 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_1 \} \}^2 \right\} \\
=\:& \cos^2 \theta_1 \cos^2 \theta_2 + \sin^2 \theta_1 \cos^2 \theta_2 + \sin^2 \theta_2 \\
=\:& 1 \\
\end{align}
\]
■ \((\partial_2^2 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_2 \} \}^2 \right\} \\
=\:& \frac{1}{s^2}\frac{\sin^2 \theta_1}{\cos^2 \theta_2} + \frac{1}{s^2}\frac{\cos^2 \theta_1}{\cos^2 \theta_2} \\
=\:& \frac{1}{s^2}\frac{1}{\cos^2 \theta_2} \\
\end{align}
\]
■ \((\partial_3^2 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_3 \} \}^2 \right\} \\
=\:& \frac{1}{s^2}\cos^2 \theta_1 \sin^2 \theta_2 + \frac{1}{s^2} \sin^2 \theta_1 \sin^2 \theta_2 + \frac{1}{s^2} \cos^2 \theta_2 \\
=\:& \frac{1}{s^2} \\
\end{align}
\]
■ \((\partial_1 \partial_2 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_1 \} \}\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_2 \} \}\right\} \\
=\:& \cos \theta_1 \cos \theta_2 \cdot \left( -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} \right) + \sin \theta_1 \cos \theta_2 \cdot \left( \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right) + 0 \\
=\:& 0 \\
\end{align}
\]
■ \((\partial_1 \partial_3 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_1 \} \}\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_3 \} \}\right\} \\
=\:& \cos \theta_1 \cos \theta_2 \cdot \left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right) + \sin \theta_1 \cos \theta_2 \cdot \left( -\frac{1}{s} \sin \theta_1 \sin \theta_2 \right) + \sin \theta_2 \cdot \left( \frac{1}{s} \cos \theta_2 \right) \\
=\:& -\frac{1}{s} \cos^2 \theta_1 \cos \theta_2 \sin \theta_2 - \frac{1}{s} \sin^2 \theta_1 \cos \theta_2 \sin \theta_2 + \frac{1}{s} \cos \theta_2 \sin \theta_2 \\
=\:& 0 \\
\end{align}
\]
■ \((\partial_2 \partial_3 \varphi)(s,\theta_1, \theta_2)\) の係数
\[
\begin{align}
& \sum_{i} \left\{ \{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_2 \} \}\{ \boldsymbol{e}_i\cdot \{ B(s,\theta_1, \theta_2) \boldsymbol{e}_3 \} \}\right\} \\
=\:& \left( -\frac{1}{s} \frac{\sin \theta_1}{\cos \theta_2} \right) \cdot \left( -\frac{1}{s} \cos \theta_1 \sin \theta_2 \right) + \left( \frac{1}{s} \frac{\cos \theta_1}{\cos \theta_2} \right) \cdot \left( -\frac{1}{s} \sin \theta_1 \sin \theta_2 \right) + 0 \\
=\:& 0 \\
\end{align}
\]
以上を纏めると、
\[
\begin{align}
(\nabla^2 \eta)\circ j &= \lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) - \frac{1}{s^2}\frac{\sin \theta_2}{\cos \theta_2} (\partial_2 \varphi)(s,\theta_1, \theta_2) + (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2 \cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} (\partial_3^2 \varphi)(s,\theta_1, \theta_2) \right\} \\
&= \lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{ -\frac{\sin \theta_2}{\cos \theta_2} (\partial_2 \varphi)(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) + (\partial_3^2 \varphi)(s,\theta_1, \theta_2) \right\} \right\} \\
&= \lambda \langle s,\theta_1, \theta_2 \rangle.\left\{ (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{ \frac{1}{\cos \theta_2} (\partial_3 ((\cos \circ {\rm pr}_3) \cdot \partial_3 \varphi))(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) \right\} \right\}
\end{align} \\
\]
つまり、
\[
\begin{align}
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} ((\nabla^2 \eta)\circ j)(s,\theta_1, \theta_2) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\varphi(s,\theta_1, \theta_2) \\
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} \left(\lambda \langle s',\theta_1', \theta_2' \rangle.\left\{ (\partial_1^2 \varphi)(s',\theta_1', \theta_2') + \frac{2}{s}(\partial_1 \varphi)(s',\theta_1', \theta_2') + \frac{1}{{s'}^2} \left\{ \frac{1}{\cos \theta_2'} (\partial_3 ((\cos \circ {\rm pr}_3) \cdot \partial_3 \varphi))(s',\theta_1', \theta_2') + \frac{1}{\cos^2 \theta_2'} (\partial_2^2 \varphi)(s',\theta_1', \theta_2') \right\} \right\}\right)(s,\theta_1, \theta_2) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\varphi(s,\theta_1, \theta_2) \\
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} \left( (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{ \frac{1}{\cos \theta_2} (\partial_3 ((\cos \circ {\rm pr}_3) \cdot \partial_3 \varphi))(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\varphi(s,\theta_1, \theta_2) \\
\end{align}
\]
\(\| j(s,\theta_1, \theta_2) \|\) について、\(\eta\) の入力が変位ベクトルであるため、基準点を \(\boldsymbol{0}\) にとることにすれば
\[
\begin{align}
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} \left( (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{ \frac{1}{\cos \theta_2} (\partial_3 ((\cos \circ {\rm pr}_3) \cdot \partial_3 \varphi))(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \| j(s,\theta_1, \theta_2) \|}\varphi(s,\theta_1, \theta_2) \\
E\cdot\varphi(s,\theta_1, \theta_2) &= -\frac{\hbar^2}{2\mu} \left( (\partial_1^2 \varphi)(s,\theta_1, \theta_2) + \frac{2}{s}(\partial_1 \varphi)(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{ \frac{1}{\cos \theta_2} (\partial_3 ((\cos \circ {\rm pr}_3) \cdot \partial_3 \varphi))(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} (\partial_2^2 \varphi)(s,\theta_1, \theta_2) \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot s}\varphi(s,\theta_1, \theta_2) \\
\end{align}
\]
が得られる。
表記を従来のものに合わせる
以下のような糖衣構文を導入する。
\[
\begin{align}
\frac{\partial^n f}{\partial s^n} &:= \partial_1^n f \\
\frac{\partial^n f}{\partial \theta_1^n} &:= \partial_2^n f \\
\frac{\partial^n f}{\partial \theta_2^n} &:= \partial_3^n f \\
\frac{\partial^n}{\partial s^n} [{\rm expr}] &:= \partial_1^n(\lambda \langle s,\theta_1, \theta_2 \rangle.\{[{\rm expr}]\}) \\
\frac{\partial^n}{\partial \theta_1^n} [{\rm expr}] &:= \partial_2^n(\lambda \langle s,\theta_1, \theta_2 \rangle.\{[{\rm expr}]\}) \\
\frac{\partial^n}{\partial \theta_2^n} [{\rm expr}] &:= \partial_3^n(\lambda \langle s,\theta_1, \theta_2 \rangle.\{[{\rm expr}]\}) \\
\end{align}
\]
これらを使うと、方程式を以下のように書き直すことができる。
\[
E\cdot\varphi(s,\theta_1, \theta_2) = -\frac{\hbar^2}{2\mu} \left( \frac{\partial^2 \varphi}{\partial s^2}(s,\theta_1, \theta_2) + \frac{2}{s}\frac{\partial \varphi}{\partial s}(s,\theta_1, \theta_2) + \frac{1}{s^2} \left\{\frac{1}{\cos \theta_2} \frac{\partial}{\partial \theta_2} \left\{ \cos \theta_2 \cdot \frac{\partial \varphi}{\partial \theta_2}(s,\theta_1, \theta_2) \right\}(s,\theta_1, \theta_2) + \frac{1}{\cos^2 \theta_2} \frac{\partial^2 \varphi}{\partial \theta_1^2}(s,\theta_1, \theta_2) \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot s}\varphi(s,\theta_1, \theta_2)
\]
曖昧さが入ることを妥協し、値の適用箇所を省略すると
\[
E\cdot\varphi = -\frac{\hbar^2}{2\mu} \left( \frac{\partial^2 \varphi}{\partial s^2} + \frac{2}{s}\frac{\partial \varphi}{\partial s} + \frac{1}{s^2} \left\{\frac{1}{\cos \theta_2} \frac{\partial}{\partial \theta_2} \left\{ \cos \theta_2 \cdot \frac{\partial \varphi}{\partial \theta_2} \right\} + \frac{1}{\cos^2 \theta_2} \frac{\partial^2 \varphi}{\partial \theta_1^2} \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot s}\varphi
\]
ここでさらに
\[
\begin{align}
r &:= s \\
\theta &:= \frac{\pi}{2} - \theta_2 \\
\phi &:= \theta_1 \\
\end{align}
\]
と置き、\(\varphi\) とその関数にこの入力の変換を合成した関数とを同一の記号で表した上で形式的に式をいじれば
\[
\begin{align}
\frac{\partial \varphi}{\partial r} &= \frac{\partial \varphi}{\partial s} \\
\frac{\partial \varphi}{\partial \theta} &= -\frac{\partial \varphi}{\partial \theta_2} \\
\frac{\partial \varphi}{\partial \phi} &= \frac{\partial \varphi}{\partial \theta_1} \\
\end{align}
\]
より
\[
\begin{align}
E\cdot\varphi &= -\frac{\hbar^2}{2\mu} \left( \frac{\partial^2 \varphi}{\partial r^2} + \frac{2}{r}\frac{\partial \varphi}{\partial r} + \frac{1}{r^2} \left\{\frac{1}{\cos (\theta + \frac{\pi}{2})} \left( -\frac{\partial}{\partial \theta} \left\{ \cos (\theta + \frac{\pi}{2}) \cdot \left( -\frac{\partial \varphi}{\partial \theta}\right) \right\}\right) + \frac{1}{(\cos(\theta + \frac{\pi}{2}))^2} \frac{\partial^2 \varphi}{\partial \phi} \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot r}\varphi \\
E\cdot\varphi &= -\frac{\hbar^2}{2\mu} \left( \frac{\partial^2 \varphi}{\partial r^2} + \frac{2}{r}\frac{\partial \varphi}{\partial r} + \frac{1}{r^2} \left\{\frac{1}{-\sin \theta} \left( -\frac{\partial}{\partial \theta} \left\{ (-\sin \theta) \cdot \left( -\frac{\partial \varphi}{\partial \theta}\right) \right\}\right) + \frac{1}{(-\sin \theta)^2} \frac{\partial^2 \varphi}{\partial \phi} \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot r}\varphi \\
E\cdot\varphi &= -\frac{\hbar^2}{2\mu} \left( \frac{\partial^2 \varphi}{\partial r^2} + \frac{2}{r}\frac{\partial \varphi}{\partial r} + \frac{1}{r^2} \left\{\frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \cdot \frac{\partial \varphi}{\partial \theta} \right) + \frac{1}{\sin^2 \theta} \frac{\partial^2 \varphi}{\partial \phi} \right\} \right) - \frac{e^2}{4\pi \varepsilon_0 \cdot r}\varphi \\
\end{align}
\]
タグ一覧:
