雑記帳
量子力学的に粒子の運動を追いかける - 自由粒子に対するシュレーディンガー方程式
目次
•
•
(書きかけ)
添書き
ここで行っている自由粒子の挙動の解析は、僕が高専で理論物理学 (応用物理) を学んだ時の担当の先生だった、宇治野秀晃先生が作成した補足資料を参考にしながら纏めている。
またその資料と全く同じ方法ではオリジナリティーが無いため、この記事では運動量 (波数) の方ではなく位置の方に注目して「(位置と運動量がある程度決まった) 自由粒子の振舞いを記述する式」の導出を行ってみてはいるものの、やっていることは基本的に変わらない。
自由粒子に対するシュレーディンガー方程式
古典力学ライクな物体の運動の解析を量子力学的にできないのか?
古典力学では、
- 初期位置
- 初速度 (初期運動量)
の2つの初期条件を与えることで、物体の運動の軌跡を具体的に求めることができた。
一方、量子力学でも同様にそういった「物体の運動の様子を追跡する」ということはできないのだろうか。
「シュレーディンガー方程式 (Schrödinger equation)」というと、「与えられた系での定常状態を求めるツール」としての側面ばかり注目されるが、「その系の量子状態の時間発展を記述する方程式」という大本の方程式にまで戻って考えると、古典力学的な物体の運動の解析に近いことを量子力学的に行うことができる。
一点周りに集中する振幅を物体のようなものと見做せる?
「系のある一点周りに振幅が集中している量子状態」というのを与えて、その量子状態の時間発展をシュレーディンガー方程式を使って追跡すれば、「一点周りに集中する振幅の追跡」として「古典力学的な物体の運動のようなもの」を解析することが (理論的には) 出来ることになる。
余談
ここではファインマン物理学で読んだ「波動関数を状態ベクトルの成分表示として考える」という流儀を採用しているため「一点周りに集中する振幅の追跡」という説明をしているが、敢えて馴染み深い語彙を使うとするならば、波束の動きを追跡するということである。
ここで注意点を挙げておくと、そういった「量子力学的な物体の挙動の追跡」は「古典力学的な物体の挙動の追跡」と比べて決定的に異なる点がある。
古典力学の場合、物体それ自体が固有の「位置」と「運動量」という物理量を一意に持つため、一つしかない物体が複数個所に同時に存在するという状況は考えられない。
その一方で、量子力学的なアプローチで考える場合、たとえ「1粒子系」であったとしても「振幅の集中する点が複数存在している状態があり得る」ということである。
- そんな非現実的なことを考える意味が果たしてあるのか?
と思うかもしれないが、現実問題としてそのような振舞いをする粒子を相手にしなければならない場面は珍しくない。
典型的なのは、磁場 (ベクトルポテンシャル) 中での粒子の挙動である。
例えば、そういったベクトルポテンシャルを伴う系の量子状態について
- 初期状態として「ある特定の位置近傍だけに振幅が集中している量子状態」を考え、その状態の時間発展を追いかけていくと、元々1か所でのみ集中していた振幅の塊が複数個に分裂する
という奇妙な振舞いを起こすことがある。(これについては、後々量子スピンに関する記事を書くときに説明する。)
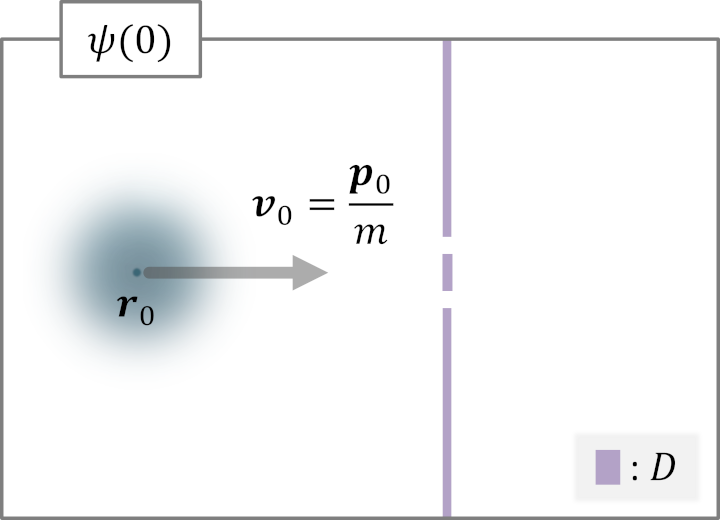
他にも、振幅の塊を有限高さのポテンシャルの壁に衝突させた場合でも「乗り越えられない振幅の塊」と「乗り越えていく振幅の塊」の2つに分裂する状態の時間発展を辿る。
以下は振幅の塊がポテンシャルの勾配に差し掛かる瞬間の量子状態の時間発展を数値計算したものである。(雑な数値計算であるため厳密解と大きく異なる可能性は否定できない。)
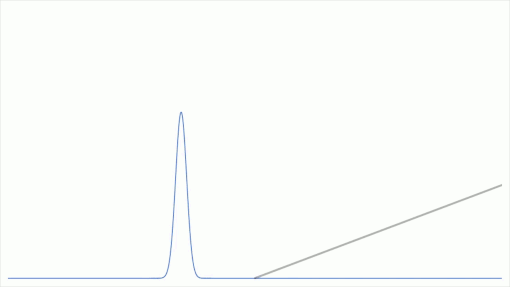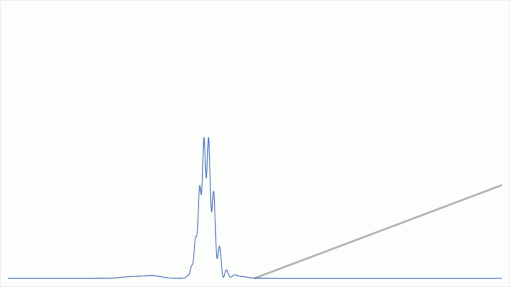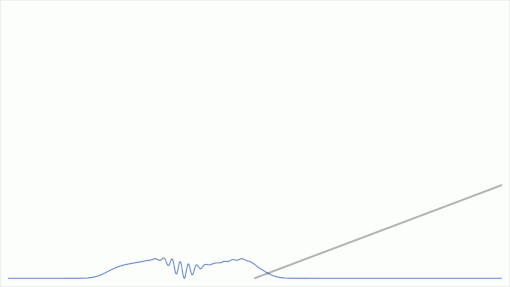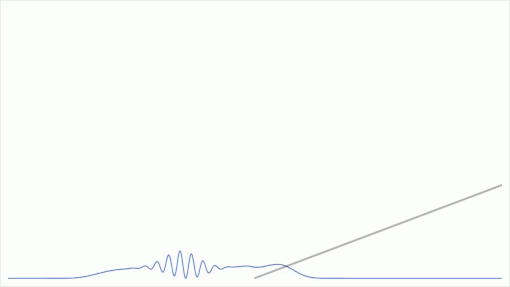
余談
振幅の塊がある量子状態は一般に「エネルギーが不確定」であるため、有限高さのエネルギーの壁を乗り越えてくる振幅が存在してしまうということは、そこまで受け入れ難いことではないはずである。
因みに、有名な「2重スリットの実験」も理論上はシュレーディンガー方程式を使って説明することができる。
具体的には
\[
V(\boldsymbol{r},t) =
\begin{cases}
\infty & \text{ if } \boldsymbol{r} \in D \\
0 & \text{ otherwise }
\end{cases}
\]
というように \(V\) を与えると、勾配が無限大のエネルギーの壁として二重スリットの形状をしたポテンシャル障壁が作れる。
ここで、シュレーディンガー方程式が正しいとするならば、「運動量 \(\boldsymbol{p}_0\) を持った物体のような振舞いをする、位置 \(\boldsymbol{r}_0\) の周辺に集中する振幅の塊が存在する量子状態 (具体的な定義は後述)」を初期状態に考え、シュレーディンガー方程式を用いて時間発展を追っていくと、その振幅の集中がスリットの両側の穴を突き抜け、さらにその突き抜けた先で分岐した振幅同士が干渉し合うといったような状態の時間発展を辿らなければらならない。(実際に解析的に解くことができるのかはわからないが、数値的に近似解を求めるアプローチであれば通用するのではないかと思われる。また厳密に言うと、そもそもこのポテンシャル中でその初期値は取れないので、以上の説明には多少の粗がある。)
また「途中で観測行為を行う」という部分についても、(光子を衝突させるなどして) 観測を行った時点で、その系の量子状態が攪乱され、観測成功後は「その観測された位置周辺に振幅が集中している状態」へと変化させられる。つまりそれを新たな初期条件に再び時間発展を追うことになるため、シュレーディンガー方程式を使って考えたとしても、現実世界での実験結果に反することのない結果が導かれる。
シュレーディンガー方程式を用いて自由粒子の運動を具体的に追跡してみる。
色々と言葉を連ねてきたが、具体的に解ける例が全くないと信じ難いだろうと思うので、具体的に「振幅の塊の挙動」をシュレーディンガー方程式を用いて解析していく。
古典力学のノリで考えると
- 自由粒子の方程式?そんな自明過ぎることをあえて議論する必要性あるの?
と考えたくなるが、「物体の存在する一点を追いかける古典力学」に対して、「物体が存在し得る全ての位置に対する振幅を同時並行で追いかける量子力学」では、そんな自明なことですら解析することが困難になる。
詳しくは、具体的な議論を追いかけていくなかでわかってくるはずである。
運動量と位置が一定の誤差の中で定まっている量子状態
まずシュレーディンガー方程式を解く前に、その一般解の初期値として与えることになる、「運動量と位置が一定の誤差の中で定まっている量子状態」について説明する。
まずパッと思いつくのは、
\[
\begin{align}
\psi &= \int_{{\mathbb{R}}^3} d \boldsymbol{r} \left\{\frac{1}{\sqrt{(2\pi)^3(\Delta r_0)^2)}} e^{-\frac{\| \boldsymbol{r} - \boldsymbol{r}_0 \|^2}{2(\Delta r_0)^2}} [{\rm position}\colon\boldsymbol{r}] \right\} \\
&= \int_{{\mathbb{R}}^3} d \boldsymbol{r} \left\{ \frac{1}{\sqrt{(2\pi)^3(\Delta r_0)^2)}} e^{-\frac{\| \boldsymbol{r} - \boldsymbol{r}_0 \|^2}{2(\Delta r_0)^2}} | \boldsymbol{r} \rangle \right\} \\
\end{align}
\]
という「振幅の分布がガウス分布となるように重ね合わせた状態」である。一見すると、これで良いような気もするが、量子力学は「位置と運動量が不可分」という古典力学とは異なった特徴を持つ点を思い出してほしい。
つまり、そうして得られた上の量子状態には既に特定の運動量の情報が組み込まれてしまっている。
ではどこに組み込まれているのかというと、複素数として表されている振幅の「位相」の部分である。
(..)
纏めると、「運動量 \(\boldsymbol{p}_0\) を持った物体のような振舞いをする、位置 \(\boldsymbol{r}_0\) の近傍に標準偏差 \(\Delta r_0\) で集中している振幅の塊が存在する量子状態 \(\psi\)」というのは
\[
\begin{align}
\psi &= \int_{{\mathbb{R}}^3} d \boldsymbol{r} \left\{ e^{-\frac{1}{i\hbar} \boldsymbol{p}_0\cdot (\boldsymbol{r}-\boldsymbol{r}_0)}\cdot \frac{1}{\sqrt{(2\pi)^3(\Delta r_0)^2)}} e^{-\frac{\| \boldsymbol{r} - \boldsymbol{r}_0 \|^2}{2(\Delta r_0)^2}} [{\rm position}\colon\boldsymbol{r}] \right\} \\
&= \int_{{\mathbb{R}}^3} d \boldsymbol{r} \left\{ e^{-\frac{1}{i\hbar} \boldsymbol{p}_0\cdot (\boldsymbol{r}-\boldsymbol{r}_0)}\cdot \frac{1}{\sqrt{(2\pi)^3(\Delta r_0)^2)}} e^{-\frac{\| \boldsymbol{r} - \boldsymbol{r}_0 \|^2}{2(\Delta r_0)^2}} | \boldsymbol{r} \rangle \right\} \\
\end{align}
\]
として与えることができる。
また後ほど例として解く時は1次元で考えるのだが、その場合は
\[
\begin{align}
\psi &= \int_{\mathbb{R}} dx \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{(2\pi)^1(\Delta x_0)^2}} e^{-\frac{| x - x_0 |^2}{2(\Delta x_0)^2}} [{\rm position}\colon x] \right\} \\
&= \int_{-\infty}^{\infty} dx \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} | x \rangle \right\} \\
\end{align}
\]
である。
余談
わかりやすくするために、この段階では状態ベクトルを規格化していないが、これについては問題ない。
というのも、シュレーディンガー方程式に従う状態の時間発展において初期条件として与えた状態ベクトルの大きさは保存され続けるという事実があり、「解を求めた後に初期状態のベクトルの大きさで割ってあげる」という形で、後から修正が利く。
自由粒子に対するシュレーディンガー方程式
1次元で考える場合、質量 \(m\) の自由粒子に対するシュレーディンガー方程式、つまり「自明なポテンシャル中の質量 \(m\) の1つの粒子だけからなる系に関する量子状態 \(\psi(t)\) の時間発展を記述する方程式」は
\[
\begin{align}
i\hbar \frac{\partial \psi}{\partial t}(t) &= H(\psi(t)) \\
\langle [{\rm position}\colon x] ,H(\psi(t)) \rangle &= -\frac{\hbar^2}{2m} \frac{\partial^2 (\lambda x.\langle [{\rm position}\colon x] ,\psi(t) \rangle)}{\partial x^2}(x)
\end{align}
\]
として与えられる。
ここで、
\[
C_{\psi}(x,t) := \langle [{\rm position}\colon x] ,\psi(t) \rangle
\]
として与えられる状態ベクトルの成分に関する方程式に書き換えると
\[
i\hbar \frac{\partial C_{\psi}}{\partial t}(x,t) = -\frac{\hbar^2}{2m} \frac{\partial^2 C_{\psi}}{\partial x^2}(x,t)
\]
である。
シュレーディンガー方程式の一般解を求める
では先ほどの方程式を解いていく。
まず、未知の関数が以下の逆フーリエ変換の形で書けるものと考える。
\[
C_{\psi}(x,t) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \hat{C}_{\psi}(\xi,t) e^{ix\xi} d\xi
\]
この式を方程式に代入すると、
\[
\begin{align}
\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( i\hbar \frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) \right) e^{ix\xi} d\xi &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( -\frac{\hbar^2}{2m} \left((i\xi)^2 \hat{C}_{\psi}(\xi,t) \right) \right) e^{ix\xi} d\xi \\
\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left\{ \left( i\hbar \frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) \right) - \left( -\frac{\hbar^2}{2m} \left((i\xi)^2 \hat{C}_{\psi}(\xi,t) \right) \right) \right\} e^{ix\xi} d\xi &= 0 \\
\end{align}
\]
両辺のフーリエ変換を考えてあげると
\[
\begin{align}
\left( i\hbar \frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) \right) - \left( -\frac{\hbar^2}{2m} \left((i\xi)^2 \hat{C}_{\psi}(\xi,t) \right) \right) &= 0 \\
\left( i\hbar \frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) \right) &= \left( -\frac{\hbar^2}{2m} \left((i\xi)^2 \hat{C}_{\psi}(\xi,t) \right) \right) \\
i\hbar \frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) &= \frac{\hbar^2\xi^2}{2m} \hat{C}_{\psi}(\xi,t) \\
\frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) &= \frac{1}{i\hbar}\frac{\hbar^2\xi^2}{2m} \hat{C}_{\psi}(\xi,t) \\
\frac{\partial \hat{C}_{\psi}}{\partial t}(\xi,t) &= -i\frac{\hbar\xi^2}{2m} \hat{C}_{\psi}(\xi,t) \\
\hat{C}_{\psi}(\xi,t) &= A(\xi) e^{-i\frac{\hbar\xi^2}{2m}t} \\
C_{\psi}(x,t) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( A(\xi) e^{-i\frac{\hbar\xi^2}{2m}t} \right) e^{ix\xi} d\xi
\end{align}
\]
任意関数を含む解が求まった。
一般解に初期条件を適用する
初期値 \(\psi(0)\) として考えたいのは、「運動量 \(p_0\) を持った物体のような振舞いをする、位置 \(x_0\) の近傍に標準偏差 \(\Delta x_0\) で集中している振幅の塊が存在する量子状態」である。
つまり
\[
\psi(0) = \int_{-\infty}^{\infty} dx \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} [{\rm position}\colon x] \right\}
\]
が初期条件である。
もう少し変形すると
\[
\begin{align}
\psi(0) &= \int_{-\infty}^{\infty}dx \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} [{\rm position}\colon x] \right\} \\
\langle [{\rm position}\colon x], \psi(0) \rangle &= \langle [{\rm position}\colon x], \int_{-\infty}^{\infty}dx \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} [{\rm position}\colon x] \right\} \rangle \\
C_{\psi}(x,0) &= \langle [{\rm position}\colon x], \int_{-\infty}^{\infty}dx' \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x'-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x' - x_0)^2}{2(\Delta x_0)^2}} [{\rm position}\colon x'] \right\} \rangle \\
C_{\psi}(x,0) &= \int_{-\infty}^{\infty}dx' \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x'-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x' - x_0)^2}{2(\Delta x_0)^2}} \langle [{\rm position}\colon x], [{\rm position}\colon x'] \rangle \right\} \\
C_{\psi}(x,0) &= \int_{-\infty}^{\infty}dx' \left\{ e^{-\frac{1}{i\hbar} p_0\cdot (x'-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x' - x_0)^2}{2(\Delta x_0)^2}} \delta(x-x') \right\} \\
C_{\psi}(x,0) &= e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} \\
\end{align}
\]
というように、初期条件に対応する成分 \(C_{\psi}(x,t)\) が満たすべき条件が得られる。
この条件を先ほど求めた任意関数を含む方程式の解に適用していく。
\[
\begin{align}
C_{\psi}(x,0) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( A(\xi) e^{-i\frac{\hbar\xi^2}{2m}\cdot 0} \right) e^{ix\xi} d\xi \\
e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} A(\xi) e^{ix\xi} d\xi \\
\end{align}
\]
その両辺フーリエ変換を取ってあげれば未知関数 \(A\) が次のように求まる。
\[
A(\xi) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2)}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} \right) e^{-ix\xi} dx
\]
よって初期条件が適用された特殊解は
\[
\begin{align}
C_{\psi}(x,t) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( \left( \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \left( e^{-\frac{1}{i\hbar} p_0\cdot (x-x_0)}\cdot \frac{1}{\sqrt{2\pi(\Delta x_0)^2)}} e^{-\frac{ (x - x_0)^2}{2(\Delta x_0)^2}} \right) e^{-ix\xi} dx \right) e^{-i\frac{\hbar\xi^2}{2m}\cdot t} \right) e^{ix\xi} d\xi \\
\end{align}
\]
これを整理すると、(一応途中計算はノートには書いてあるが、打ち込むのが非常に億劫なので、今は省略。後ほど書き加えるかもしれない。)
\[
C_{\psi}(x,t) = \frac{1}{\sqrt{2\pi\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}} \exp\left(-\frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}\right) \exp\left(i\left( \frac{p_0}{\hbar}(x-x_0) - \frac{p_0^2}{2m\hbar}t \right)\right)
\]
が得られる。
余談
古典力学的に考えれば、力が作用していない物体の運動は「単なる等速直線運動」であり、非常に単純な式で記述される。そしてそのイメージが染み付いていると、「自由粒子ごときが本当にこんなに煩雑な式として記述されるのか?」を疑いたくなるだろう。
そういった場合は、この関数を「自由粒子のシュレーディンガー方程式」に代入し、愚直に微分計算を行ってみるとよい。実際に計算してみればわかるが、この関数がしっかりとその方程式の特殊解であることを確認することができる。
状態ベクトルを規格化する
議論をわかりやすくするために、初期条件に規格化されていないベクトルを指定していたが、解が求まったので最後の仕上げとしてベクトルを規格化してあげる。
\[
\begin{align}
\psi'(t) &= \frac{\psi(t)}{\| \psi(0) \|} \\
&= \frac{1}{\| \psi(0) \|} \psi(t) \\
&= \sqrt{2\sqrt{\pi}\cdot (\Delta x_0)} \int_{-\infty}^\infty dx \left\{ C_{\psi}(x,t) [{\rm position}\colon x] \right\} \\
&= \sqrt{2\sqrt{\pi}\cdot (\Delta x_0)} \int_{-\infty}^\infty dx \left\{ \frac{1}{\sqrt{2\pi\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}} \exp\left(-\frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}\right) \exp\left(i\left( \frac{p_0}{\hbar}(x-x_0) - \frac{p_0^2}{2m\hbar}t \right)\right) [{\rm position}\colon x] \right\} \\
&= \int_{-\infty}^\infty dx \left\{ \frac{\root 4 \of \pi \cdot \sqrt{(\Delta x_0)}}{\sqrt{\pi\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}} \exp\left(-\frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}\right) \exp\left(i\left( \frac{p_0}{\hbar}(x-x_0) - \frac{p_0^2}{2m\hbar}t \right)\right) [{\rm position}\colon x] \right\} \\
&= \int_{-\infty}^\infty dx \left\{ \frac{1}{\root 4 \of {\pi (\Delta x_0)^{-2} \left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)^2}} \exp\left(-\frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}\right) \exp\left(i\left( \frac{p_0}{\hbar}(x-x_0) - \frac{p_0^2}{2m\hbar}t \right)\right) |x\rangle \right\} \\
\end{align}
\]
確かめてみればわかるが、しっかりと
\[
\begin{align}
\| \psi(t) \|^2 &= \langle \psi'(t), \psi'(t) \rangle \\
&= \int_{-\infty}^\infty dx \left\{ (C_{\psi'}(x,t))^{*}\cdot C_{\psi'}(x,t) \right\} \\
&= 1
\end{align}
\]
が成り立っていることを確認することができる。
グラフを使って解の様子をイラストレーションする
先ほど求めた特殊解を実際にグラフに表してみる。
まず、位相の情報を取り除いた関数を求めると
\[
\begin{align}
|C_{\psi'}(x,t)|^2 &= \frac{1}{\sqrt{\pi (\Delta x_0)^{-2}}}\left|\frac{1}{\sqrt{\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}}\right|^2\cdot \left|\exp\left(-\frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2\left((\Delta x_0)^2 + i\frac{\hbar}{m}t\right)}\right) \exp\left(i\left( \frac{p_0}{\hbar}(x-x_0) - \frac{p_0^2}{2m\hbar}t \right)\right)\right|^2 \\
&= \frac{1}{\sqrt{\pi (\Delta x_0)^{-2}}}\exp\left(-\log\left| (\Delta x_0)^2 + i\frac{\hbar}{m}t \right|\right) \cdot \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{\left| (\Delta x_0)^2 + i\frac{\hbar}{m}t \right|^2}(\Delta x_0)^2 \right) \\
&= \frac{1}{\sqrt{\pi (\Delta x_0)^{-2}} \left| (\Delta x_0)^2 + i\frac{\hbar}{m}t \right|} \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{\left| (\Delta x_0)^2 + i\frac{\hbar}{m}t \right|^2}(\Delta x_0)^2 \right) \\
&= \frac{1}{\sqrt{\pi (\Delta x_0)^{-2}} \sqrt{(\Delta x_0)^4 + \left(\frac{\hbar}{m}t\right)^2}} \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{\left( (\Delta x_0)^4 + \left(\frac{\hbar}{m}t\right)^2 \right)}(\Delta x_0)^2 \right) \\
&= \frac{1}{\sqrt{\pi (\Delta x_0)^{-2}\left((\Delta x_0)^4 + \left(\frac{\hbar}{m}t\right)^2\right)}} \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{\left( (\Delta x_0)^4 + \left(\frac{\hbar}{m}t\right)^2 \right)}(\Delta x_0)^2 \right) \\
&= \frac{1}{\sqrt{\pi \left((\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2\right)}} \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{\left( (\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2 \right)} \right) \\
\end{align}
\]
となる。
以下は、一定間隔で時間を進めて描いた上の関数のグラフを GIF アニメーションにしたものである。

時間経過に伴う「振幅の集中度合いの緩和 (位置の不確定性の向上 / 運動量の不確定性の低下)」という特徴を強調するために、使用するパラメータを意図的に調整しているが、プランク定数 \(\hbar\) の値に対して十分大きい質量を持つ物体であれば、振幅の集中度合いの緩和は殆ど無視できるレベルとなる。逆に、電子のような質量が小さい粒子については、時間経過とともに位置の不確定性が急速に上がっていく。
位置の不確定性の時間変化を具体的に調べる
より具体的に考えると、時間 \(t\) 経過後の位置の不確定性 \((\Delta x)(t)\) は
\[
|C_{\psi'}(x,t)| = \sqrt{\frac{1}{\sqrt{\pi \left((\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2\right)}}} \exp\left(- \frac{\left( (x-x_0) - \frac{p_0}{m}t \right)^2}{2 \left(\sqrt{ (\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2 } \right)^2} \right)
\]
より
\[
(\Delta x)(t) = \sqrt{ (\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2 }
\]
であることになる。(この話は、資料で読んだ内容と重なる。)
つまり、質量の小さい粒子の例として
- \(\Delta x_0 = 0.0001[{\rm m}]\)
- \(m = 9.1093837015\times 10^{-31} [{\rm kg}]\)
を考えてみると、位置の不確定性 \(\Delta x\) が \(1[{\rm m}]\) に達するまでに要する時間は
\[
\begin{align}
(\Delta x)(t) &= \sqrt{ (\Delta x_0)^2 + \frac{\hbar^2 (\Delta x_0)^{-2}}{m^2}t^2 } \\
t &= \frac{m\cdot(\Delta x_0)}{\hbar}\sqrt{ (\Delta x)^2 - (\Delta x_0)^2 } \\
&\simeq 0.863799269 [{\rm s}] \\
\end{align}
\]
となり、1秒も経たぬうちにそのレベルにまで不確定性が拡大する。
一方で、古典力学で扱う範疇にあるような
- \(\Delta x_0 = 0.05[{\rm m}]\)
- \(m = 0.02 [{\rm kg}]\)
というものに対して同様のことを考えてみると、
\[
\begin{align}
t &= \frac{m\cdot(\Delta x_0)}{\hbar}\sqrt{ 1 - (\Delta x_0)^2 } \\
&\simeq 9.47\times 10^{30} [{\rm s}] \\
&\simeq 3 \times 10^{23} [{\rm year}] \\
\end{align}
\]
という結果が得られ、不確定性が1メートルに至るまでに約3000垓年という果てしない時間がかかることがわかる。
見ての通り、ミクロスケールで考える場合は、不確定性原理の影響が顕著に現れてくるが、マクロスケールで考えた場合、不確定性原理の影響は完全に無いわけではないものの、殆ど無視できる程度の影響しかない。
(..)
振幅の分布が一様になった粒子の性質
前のセクションで求めた特殊解について、\(t\rightarrow \infty\) の極限を考えると、位置の情報を完全に失った量子状態へと行きつくが、その状態にある粒子は、ある特定の角振動数 \(\omega\) と波数 \(k\) を持った波として捉えることができる。
ここで、
- \(E\): 自由粒子の持つ運動エネルギー
- \(p\): 自由粒子の運動量
としたとき、それらは
\[
\begin{align}
E &=\hbar \omega \\
p &= \hbar k \\
\end{align}
\]
という関係式を満たし、その波は ド・ブロイ波 (de Broglie wave) や 物質波 (matter wave) などと呼ばれる。
おまけ
球ベッセル関数と球面調和関数は?
量子力学を学んできた人の中には「自由粒子のシュレーディンガー方程式」と聞くと、球ベッセル関数と球面調和関数を用いて表された一般解を連想する人がいるかもしれないが、あくまでもその解は、ヘルムホルツ方程式 (Helmholtz equation) として出てくる「自由粒子のシュレーディンガー方程式から誘導される定常状態を求める方程式」をさらに球座標表示した際の成分に関する方程式として解いた際に得られるものである。
例えば「3次元的な球面の形状をした無限に高い井戸型ポテンシャルが存在する1粒子系における定常状態」を求める際であれば、「一旦ポテンシャルを無視して出てくるヘルムホルツ方程式の一般解を求めた後、無限に高いポテンシャルの壁の中では振幅を持たないという条件をその一般解に課すことで具体的な解の形を求める」というように、その過程で球ベッセル関数などが現れる。
しかしここで考えているのは「定常状態の式が満たすべき形」ではなく、「(エネルギーの値すら不確定な) 量子状態の時間変化」であり、それらは登場人物として出てこないという点には注意してほしい。
因みに、自由粒子の定常状態は難しく考えなくとも「任意の運動量 \(\boldsymbol{p}\) について、運動量が確定した状態 \([{\rm momentum}\colon \boldsymbol{p}]\) (見慣れた記号で表すならば \(|\boldsymbol{p}\rangle\))」である。
タグ一覧:
