雑記帳
速さの2乗に比例する空気抵抗を加味した物体の放物運動
運動方程式 (EOM: Equation Of Motion)
一般形
方程式の全容
速さの2乗に比例する空気抵抗を加味した物体の運動方程式は、
- \(m\): 物体の質量
- \(\boldsymbol{r}\): 物体の位置
- \(k\): 比例定数 (\(k > 0\))
としたとき、以下で表すことができる。
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} - \left(k\sqrt{\boldsymbol{v}\cdot \boldsymbol{v}}\right) \boldsymbol{v}
\]
方程式の立て方
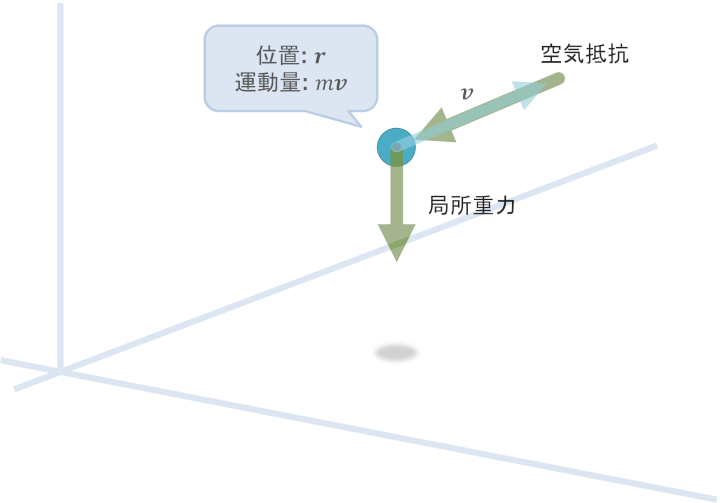
まず図を見ての通り、物体に作用する力として考えるのは以下の2つとなる。
- 局所重力 \(\boldsymbol{F}_1\)
- 速さの2乗に比例する空気抵抗 \(\boldsymbol{F}_2\)
局所重力 \(\boldsymbol{F}_1\) に関しては既に何度もやっているように
\[
\boldsymbol{F}_1 = m\boldsymbol{g}
\]
続いて、空気抵抗 \(\boldsymbol{F}_2\) についてだが、これは素直に「力の大きさ」と「力の方向」に分けて考えてみるとわかりやすい。
まず力の大きさ \(\lVert \boldsymbol{F}_2 \rVert\) は、「速さ \(\lVert \boldsymbol{v} \rVert\) の2乗 \({\lVert \boldsymbol{v} \rVert}^2\) に比例する」ということなので、比例係数を適当に \(k\) とすると、
\[
\lVert \boldsymbol{F}_2 \rVert = k\cdot {\lVert \boldsymbol{v} \rVert}^2
\]
となる。
一方で力の単位方向ベクトル \(\hat{\boldsymbol{F}_2}\) は、図を見て明らかであるが、速度と同じ方向を向く単位ベクトル \(\frac{\boldsymbol{v}}{\lVert \boldsymbol{v} \rVert}\) と逆の方向 \(-\frac{\boldsymbol{v}}{\lVert \boldsymbol{v} \rVert}\) である。
この時、速度がゼロベクトルである場合は方向が定義できない点に注意して欲しい。
つまり力の方向は、\(\boldsymbol{v} \ne \boldsymbol{0}\) としたとき、
\[
\hat{\boldsymbol{F}_2} = -\frac{\boldsymbol{v}}{\lVert \boldsymbol{v} \rVert}
\]
となる。
「力の方向」と「力の大きさ」が求まれば
\[
\boldsymbol{F}_2 = \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2}
\]
より、\(\boldsymbol{F}_2\) は \(\boldsymbol{v} \ne \boldsymbol{0}\) である場合、
\[
\begin{align}
\boldsymbol{F}_2 &= \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2} \\
&= \left( k\cdot {\lVert \boldsymbol{v} \rVert}^2 \right) \cdot \left( -\frac{\boldsymbol{v}}{\lVert \boldsymbol{v} \rVert} \right) \\
\end{align}
\]
上の式では未定義となってしまっている \(\boldsymbol{v} = \boldsymbol{0}\) のケースは、そもそも空気抵抗がかからないので
\[
\boldsymbol{F}_2 = \boldsymbol{0}
\]
とすればよい。
以上を纏めると
■ 速度が零ベクトルの場合
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g}
\]
■ 速度が零ベクトルでない場合
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} + k{\lVert\boldsymbol{v}\rVert}^2\cdot(-\frac{\boldsymbol{v}}{\lVert\boldsymbol{v}\rVert})
\]
一応はこれで方程式を立てることができたわけだが、条件分岐を含んでしまっているという点において、まだあまり好ましくない。
できることなら方程式を一本に纏められると都合がよいのだが、実際式変形をしてみれば気付くように、まさにそういったことができることに気付く。
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} - k\lVert\boldsymbol{v}\rVert \boldsymbol{v}
\]
つまり、冒頭に与えた方程式を得られた。
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} - \left(k\sqrt{\boldsymbol{v}\cdot \boldsymbol{v}}\right) \boldsymbol{v}
\]
正規直交基底に関する成分に対する方程式
方程式の全容
一般形の方程式を、ベクトルの \(x,y,z\) 成分に関する方程式として表すと以下のようになる。
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d x}{dt} \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d y}{dt} \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d z}{dt} \\
\end{align}
\]
但し、 \(\boldsymbol{e}_2 \cdot \boldsymbol{g}\) は、
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と同じ向きに設定した場合、\(g\)
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と逆の向きに設定した場合、\(-g\)
である。
一般形からの導出
先ほどの一般的な方程式について、適当な正規直交基底 \(\{\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\}\) に関する各成分に注目すると
\[
\begin{align}
\boldsymbol{e}_i \cdot \frac{d \boldsymbol{p}}{dt} &= \boldsymbol{e}_i \cdot (m\boldsymbol{g} - k\lVert\boldsymbol{v}\rVert \boldsymbol{v}) \\
\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{p})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) + \boldsymbol{e}_i \cdot (-k\lVert\boldsymbol{v}\rVert \boldsymbol{v}) \\
\frac{d (\boldsymbol{e}_i \cdot (m\cdot \boldsymbol{v}))}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) + \boldsymbol{e}_i \cdot (-k\left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d \boldsymbol{r}}{dt}) \\
m\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{v})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) - k\cdot (\boldsymbol{e}_i \cdot \left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d \boldsymbol{r}}{dt}) \\
m\frac{d^2 (\boldsymbol{e}_i \cdot \boldsymbol{r})}{{dt}^2} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) - k\cdot (\left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d (\boldsymbol{e}_i \cdot\boldsymbol{r})}{dt}) \\
\end{align}
\]
ここで、\(\boldsymbol{e}_2\) が \(\boldsymbol{g}\) と平行である (つまり、\(\boldsymbol{g}\) が \(\boldsymbol{e}_1,\boldsymbol{e}_3\) 方向に成分を持たない) とし、さらに
\[
\begin{align}
x(t) &= \boldsymbol{e}_1 \cdot \boldsymbol{r}(t) \\
y(t) &= \boldsymbol{e}_2 \cdot \boldsymbol{r}(t) \\
z(t) &= \boldsymbol{e}_3 \cdot \boldsymbol{r}(t) \\
\end{align}
\]
と置くと、次の各3つの成分に関する方程式が得られる。
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot \left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d x}{dt} \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) - k\cdot \left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d y}{dt} \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot \left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d z}{dt} \\
\end{align}
\]
ベクトルの大きさも成分を使った式で書き換えると
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d x}{dt} \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d y}{dt} \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot \sqrt{{\left( \frac{d x}{dt} \right)}^2 + {\left( \frac{d y}{dt} \right)}^2 + {\left( \frac{d z}{dt} \right)}^2} \frac{d z}{dt} \\
\end{align}
\]
よくあるミス
しばしば、速さ (の1乗) に比例する空気抵抗に関する運動方程式の成分表示の類推から、速さの2乗に比例する空気抵抗に関する運動方程式を
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot {\left( \frac{d x}{dt} \right)}^2 \\
m\frac{d^2 y}{{dt}^2} &= mg - k\cdot {\left( \frac{d y}{dt} \right)}^2 \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot {\left( \frac{d z}{dt} \right)}^2 \\
\end{align}
\]
と誤解して立ててしまうケースがあるが、これこそまさに「成分という具体的な量に気をそらされて全体像を見失ってしまっている状況」のわかりやすい一例といってよいだろう。
他のタイプの空気抵抗が作用する場合における運動の軌跡との比較
前回の「速さに比例する空気抵抗が作用する物体の放物運動」や前々回の「局所重力のみが作用する物体の放物運動」であれば、一般解を簡単に求めることができたが、残念ながらこの「速さの2乗に比例する空気抵抗が作用する物体の放物運動」はその非線形の微分方程式を見て察しが付くように、前回までのようにはいかない。
というわけで一般解を紹介できない代わりとして、このタイプの空気抵抗が作用する場合の物体の運動の軌跡が、前回・前々回のものと比較してどのように異なったものになるのかの具体例を一つ載せておく。
以下は
- 初期位置 \(\boldsymbol{r}_0\)
- 初速 \(\boldsymbol{v}_0\)
- 質量 \(m\)
- 比例定数 \(k\)
を全て統一させた中で、3つのタイプの放物運動を大雑把に数値計算してみた結果を同じグラフに落とし込んだものである。(違いがわかりやすくなるように、敢えて空気抵抗にかかる係数を大きくしてある。)
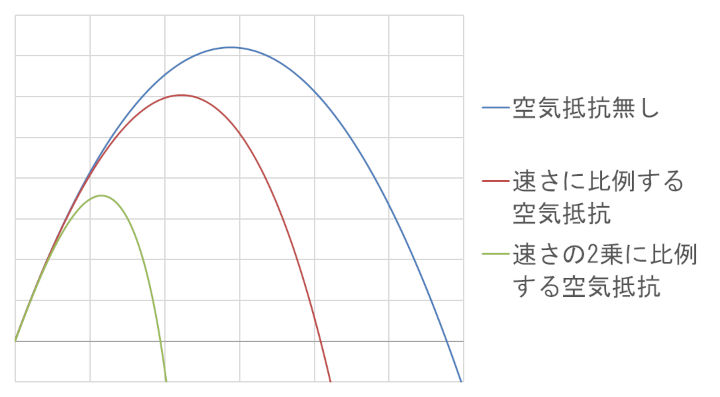
複雑な見た目の運動方程式に関わらず、このように「(厳密には違うが) 放物線っぽい軌跡」を描きながら落下していくだけの単調な運動をする。
特定の条件が課された状況下での運動方程式
運動の軌跡が重力加速度と平行な直線上のみで完結する場合
自由落下や鉛直投げ上げのような「初速が重力加速度方向以外の成分を持たないケース」の場合、運動方程式を大分簡略化して考えることができる。
まず仮定より、運動 \(\boldsymbol{r}(t)\) は、ある関数 \(\alpha(t)\) があって
\[
\boldsymbol{r}(t) = \boldsymbol{r}_0 + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
という形で書かれることになる。
この式を大本の運動方程式に代入すると
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt} &= m\boldsymbol{g} - k\lVert\boldsymbol{v}\rVert \boldsymbol{v} \\
m\frac{d^2 \boldsymbol{r}}{{dt}^2} &= m\boldsymbol{g} - k\lVert\boldsymbol{v}\rVert \boldsymbol{v} \\
m\frac{d^2 \boldsymbol{r}}{{dt}^2} &= m\boldsymbol{g} - k\left\lVert\frac{d \boldsymbol{r}}{dt}\right\rVert \frac{d \boldsymbol{r}}{dt} \\
m\frac{d^2 (\lambda t.(\boldsymbol{r}(t)))}{{dt}^2}(t) &= m\boldsymbol{g} - k\left\lVert \frac{d (\lambda t.(\boldsymbol{r}(t)))}{dt}(t) \right\rVert \frac{d (\lambda t.(\boldsymbol{r}(t)))}{dt}(t) \\
m\frac{d^2 (\lambda t.(\boldsymbol{r}_0 + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}))}{{dt}^2}(t) &= m\boldsymbol{g} - k\left\lVert \frac{d (\lambda t.(\boldsymbol{r}_0 + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}))}{dt}(t) \right\rVert \frac{d (\lambda t.(\boldsymbol{r}_0 + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}))}{dt}(t) \\
m\frac{d^2 (\lambda t.(\alpha(t)))}{{dt}^2}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\boldsymbol{g} - k\left\lVert \frac{d (\lambda t.(\alpha(t)))}{dt}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \right\rVert \frac{d (\lambda t.(\alpha(t)))}{dt}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
m\frac{d^2 \alpha}{{dt}^2}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\boldsymbol{g} - k\left\lVert \frac{d \alpha}{dt}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \right\rVert \frac{d \alpha}{dt}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
m\frac{d^2 \alpha}{{dt}^2}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\lVert \boldsymbol{g} \rVert\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} - k \left\lvert \frac{d \alpha}{dt}(t) \right\rvert \left\lVert \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \right\rVert \frac{d \alpha}{dt}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
m\frac{d^2 \alpha}{{dt}^2}(t) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= (m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt}(t) \right\rvert \frac{d \alpha}{dt}(t)) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}\\
\boldsymbol{0} &= (m\frac{d^2 \alpha}{{dt}^2}(t) - (m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt}(t) \right\rvert \frac{d \alpha}{dt}(t))) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}\\
\end{align}
\]
ここでいつものように、
- ゼロベクトルでない \(\boldsymbol{x}\) について、 \(a \boldsymbol{x} = \boldsymbol{0}\) ならば \(a = 0\) である
を使用すると、\(\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}\) はゼロベクトルでないので
\[
\begin{align}
m\frac{d^2 \alpha}{{dt}^2}(t) - (m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt}(t) \right\rvert \frac{d \alpha}{dt}(t)) &= 0 \\
m\frac{d^2 \alpha}{{dt}^2}(t) &= m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt}(t) \right\rvert \frac{d \alpha}{dt}(t) \\
\end{align}
\]
が従う。
つまり \(\alpha\) が満たすべき方程式として次の方程式が得られる。
\[
\begin{align}
m\frac{d^2 \alpha}{{dt}^2} = m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt} \right\rvert \frac{d \alpha}{dt} \\
\end{align}
\]
まだいやらしい絶対値の記号がついているとはいえ、最初のものと比較すればかなり簡略化されていて、実際適切に条件分岐を考えることでこのタイプの運動を解析的に解くことができてしまう。詳しいことは練習問題のセクションを見てほしい。
練習問題
例1: 自由落下
一般式を解析的に解くことは絶望的であるが、自由落下というのは「運動の軌跡が重力加速度と平行な直線上のみで完結する場合」に当てはまるため、そこで導出した方程式を代わりに用いることができ、それによって厳密解を得ることができる。
解きたい方程式は
\[
m\frac{d^2 \alpha}{{dt}^2} = m\lVert \boldsymbol{g} \rVert - k \left\lvert \frac{d \alpha}{dt} \right\rvert \frac{d \alpha}{dt}
\]
である。
まずは絶対値の記号を外したいのだが、そのためにまず \(\alpha\) の意味を振り返る。
\[
\boldsymbol{r}(t) = \boldsymbol{r}_0 + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
\(r_0\) の与え方は任意である以上、\(\alpha(t)\) そのものの符号自体は特別な意味を持たないが、その時間変化である \(\frac{d \alpha}{dt}\) については
- 「\(\alpha\) が増加する」というのは「物体が重力加速度の方向に進んでいる」
という見方ができる。
今考えたいのは自由落下であり、重力加速度の方向にのみ物体が進んでいくことがわかっている。言い換えれば、
\[
\frac{d \alpha}{dt}(t) \ge 0
\]
が任意の \(t\) に対して成り立つということであり、そしてこの条件から
\[
\left\lvert \frac{d \alpha}{dt} \right\rvert = \frac{d \alpha}{dt}
\]
というようにして絶対値の記号を外せることがわかる。
よって解くべき方程式は
\[
m\frac{d^2 \alpha}{{dt}^2} = mg - k \left( \frac{d \alpha}{dt} \right)^2
\]
(但し、\(g := \lVert \boldsymbol{g} \rVert\))
である。
この方程式を解いていく。
まず
\[
A(t):= \frac{d \alpha}{dt}(t)
\]
と置くと
\[
\begin{align}
m\frac{d A}{dt} &= mg - k A^2 \\
A(t) &= \sqrt{\frac{mg}{k}} \tanh\left( \sqrt{\frac{mg}{k}}\cdot \left( \frac{k}{m} t + C \right) \right) \\
\frac{d \alpha}{dt}(t) &= \sqrt{\frac{mg}{k}} \tanh\left( \sqrt{\frac{mg}{k}}\cdot \left( \frac{k}{m} t + C_1 \right) \right) \\
\alpha(t) &= \int \sqrt{\frac{mg}{k}} \tanh\left( \sqrt{\frac{mg}{k}}\cdot \left( \frac{k}{m} t + C_1 \right) \right) \, dt + C_2 \\
\end{align}
\]
(// 上の積分は初等関数の組み合わせとして表される関数として求めることはできるのだが、書き下すのが大変なので一旦後回し)
例2: 鉛直投げ上げ
鉛直投げ上げも「運動の軌跡が重力加速度と平行な直線上のみで完結する場合」に当てはまるが、こちらは少しトリッキーとなる。
というのも
- 絶対値の記号を外したい場合、運動の方向が変わると、方程式も変わってしまう
ためである。
自由落下の例で説明したが、運動の方向が重力加速度に対して順方向である場合
\[
m\frac{d^2 \alpha}{{dt}^2} = mg - k \left( \frac{d \alpha}{dt} \right)^2
\]
という方程式で記述される。
一方で、投げ上げられている最中は、運動の方向が重力加速度に対して逆方向である、つまり
\[
\frac{d \alpha}{dt}(t) \le 0
\]
であり、絶対値の記号を外す際に、マイナスの記号がかかってしまう。
つまり投げ上げられている最中の方程式は
\[
m\frac{d^2 \alpha}{{dt}^2} = mg + k \left( \frac{d \alpha}{dt} \right)^2
\]
となる。
タグ一覧:
