雑記帳
速さに比例する空気抵抗を加味した物体の放物運動
運動方程式 (EOM: Equation Of Motion)
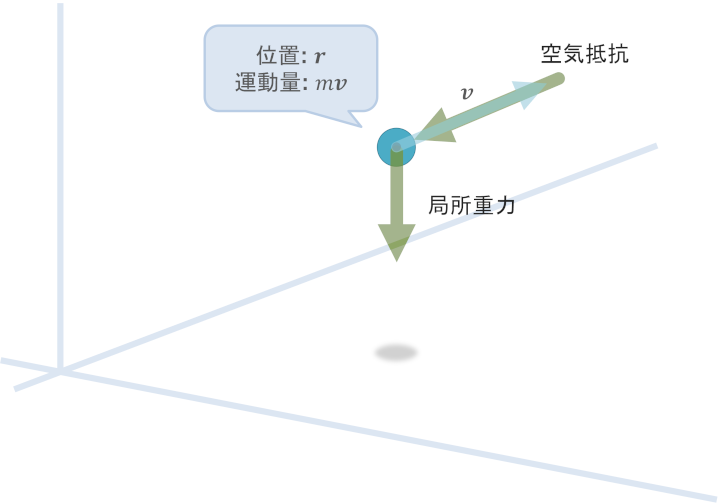
一般形
方程式の全容
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} + (-k\boldsymbol{v})
\]
正規直交基底に関する成分に対する方程式
方程式の全容
一般形の方程式を、ベクトルの \(x,y,z\) 成分に関する方程式として表すと以下のようになる。
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot \frac{d x}{dt} \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) - k\cdot \frac{d y}{dt} \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot \frac{d z}{dt} \\
\end{align}
\]
但し、 \(\boldsymbol{e}_2 \cdot \boldsymbol{g}\) は、
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と同じ向きに設定した場合、\(g\)
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と逆の向きに設定した場合、\(-g\)
である。
一般形からの導出
先ほどの一般的な方程式対し、適当な正規直交基底 \(\{\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\}\) に関する各成分に注目すると
\[
\begin{align}
\boldsymbol{e}_i \cdot \frac{d \boldsymbol{p}}{dt} &= \boldsymbol{e}_i \cdot (m\boldsymbol{g} + (-k\boldsymbol{v})) \\
\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{p})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) + \boldsymbol{e}_i \cdot (-k\boldsymbol{v}) \\
\frac{d (\boldsymbol{e}_i \cdot (m\cdot \boldsymbol{v}))}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) + \boldsymbol{e}_i \cdot (-k\frac{d \boldsymbol{r}}{dt}) \\
m\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{v})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) - k\cdot (\boldsymbol{e}_i \cdot \frac{d \boldsymbol{r}}{dt}) \\
m\frac{d^2 (\boldsymbol{e}_i \cdot \boldsymbol{r})}{{dt}^2} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) - k\cdot \frac{d (\boldsymbol{e}_i \cdot\boldsymbol{r})}{dt} \\
\end{align}
\]
ここで、\(\boldsymbol{e}_2\) が \(\boldsymbol{g}\) と平行である (つまり、\(\boldsymbol{g}\) が \(\boldsymbol{e}_1,\boldsymbol{e}_3\) 方向に成分を持たない) とし、さらに
\[
\begin{align}
x(t) &= \boldsymbol{e}_1 \cdot \boldsymbol{r}(t) \\
y(t) &= \boldsymbol{e}_2 \cdot \boldsymbol{r}(t) \\
z(t) &= \boldsymbol{e}_3 \cdot \boldsymbol{r}(t) \\
\end{align}
\]
と置くと、先に示したの各3つの成分に関する方程式が得られる。
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= - k\cdot \frac{d x}{dt} \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) - k\cdot \frac{d y}{dt} \\
m\frac{d^2 z}{{dt}^2} &= - k\cdot \frac{d z}{dt} \\
\end{align}
\]
方程式の一般解を求める
一般形
運動方程式
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} + (-k\boldsymbol{v})
\]
の一般解を求める。
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt} &= m\boldsymbol{g} + (-k\boldsymbol{v}) \\
m\frac{d \boldsymbol{v}}{dt} &= -k\cdot(\boldsymbol{v} - \frac{m\boldsymbol{g}}{k}) \\
\frac{d \boldsymbol{v}}{dt} &= -\frac{k}{m}\cdot(\boldsymbol{v} - \frac{m\boldsymbol{g}}{k}) \\
\end{align}
\]
ここで
\[
\boldsymbol{V}(t) := \boldsymbol{v}(t) - \frac{m\boldsymbol{g}}{k}
\]
と置くと
\[
\frac{d \boldsymbol{V}}{dt} = \frac{d \boldsymbol{v}}{dt} - \boldsymbol{0}
\]
より
\[
\begin{align}
\frac{d \boldsymbol{v}}{dt} &= -\frac{k}{m}\cdot(\boldsymbol{v} - \frac{m\boldsymbol{g}}{k}) \\
\frac{d \boldsymbol{V}}{dt} &= -\frac{k}{m}\cdot \boldsymbol{V} \\
\boldsymbol{V}(t) &= \boldsymbol{\alpha}_1\cdot e^{-\frac{k}{m}t} \\
\boldsymbol{v}(t) - \frac{m\boldsymbol{g}}{k} &= \boldsymbol{\alpha}_1\cdot e^{-\frac{k}{m}t} \\
\boldsymbol{v}(t) &= \frac{m\boldsymbol{g}}{k} + \boldsymbol{\alpha}_1\cdot e^{-\frac{k}{m}t} \\
\frac{d \boldsymbol{r}}{dt}(t) &= \frac{m\boldsymbol{g}}{k} + \boldsymbol{\alpha}_1\cdot e^{-\frac{k}{m}t} \\
\boldsymbol{r}(t) &= \frac{m\boldsymbol{g}}{k}t -\frac{m}{k} \boldsymbol{\alpha}_1\cdot e^{-\frac{k}{m}t} + \boldsymbol{\alpha}_2 \\
\end{align}
\]
空気抵抗を考えない場合と決定的に異なるのは、
- 空気抵抗を考えないモデルの場合: 際限なく加速していく
- 空気抵抗を加味するモデルの場合: 一定の速さまでしか加速できない (その頭打ちとなる速さは、終端速度と呼ばれる。)
という点である。
実際、速度の式 \(\boldsymbol{v}(t)\) に対して \(t\rightarrow \infty\) の極限を撮ってみればわかるように
\[
\lim_{t\rightarrow\infty} \boldsymbol{v}(t) = \frac{m\boldsymbol{g}}{k}
\]
というように有限の速さ \(\frac{mg}{k}\) を持った速度に収束することがわかる。
練習問題
(..)
タグ一覧:
