雑記帳
局所重力だけが作用する物体の運動
運動方程式 (EOM: Equation Of Motion)
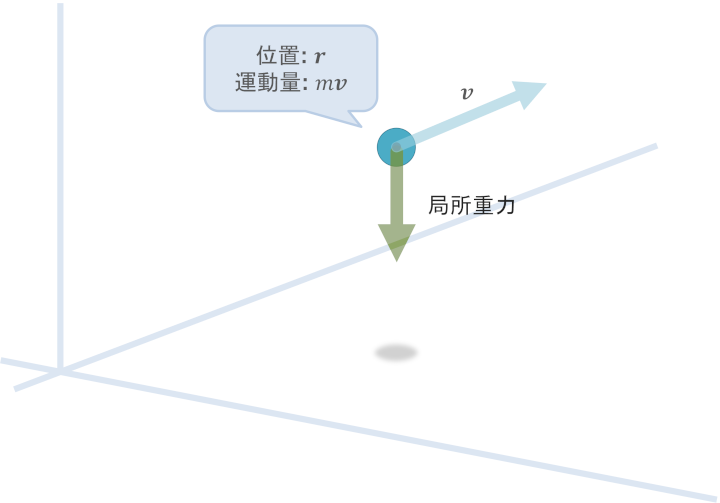
一般形
方程式の全容
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g}
\]
方程式を立てる際の注意
まず、ベクトルを積極的に用いないスタイルで物理学を学んできた人からすると、この方程式を見たときに
- どうして重力は下向きに働いているのに、マイナスの符号がついてないのか?
- その重力加速度は、その重力加速度と平行な座標軸に対して順方向を向いているのか、それとも逆方向を向いているのか。
などといったことを疑問に思うかもしれない。
これについて補足しておくと、そもそも
- 重力加速度の方向を定めるために座標軸の設定をする
という部分で定義の循環が起きている。
第一に (幾何) ベクトルというのは、大きさと方向を持った量である。
物体の加速度と呼ばれる物理量もベクトル量であり、ここで登場している「重力"加速度" \(\boldsymbol{g}\)」というのも文字通り加速度である。つまりそれは「(加速度の) 大きさ」と「(加速度の) 方向」という2つの量を同時に持っている。
何が言いたいのかといえば、「座標軸の方向」を設定するよりも前に、「重力加速度の方向」という「特定の方向を指し示す既知量」が既に自然界の中に存在しているということである。
因みにそのことを確認するのは実は非常に簡単で、例えば手元に消しゴムがあるのであればそれを自由落下させてみてほしい。その消しゴムが進んでいく方向がまさにその「重力加速度の方向」である。そして考えてほしいのだが、その落下する方向を認知するのに別途「座標軸の設定」は必要であっただろうか?
そもそも、俗にいう「\(y\) 軸の方向の設定」というのは、まさに「自然界にある重力加速度の方向」を暗黙的に使用しているわけで、その \(y\) 軸の方向を使って加速度の方向を "定義する" というのは先ほども述べたように、話が循環しているのである。
正規直交基底に関する成分に対する方程式
先ほどの一般的な方程式対し、適当な正規直交基底 \(\{\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\}\) に関する各成分に注目すると
\[
\begin{align}
\boldsymbol{e}_i \cdot \frac{d \boldsymbol{p}}{dt} &= \boldsymbol{e}_i \cdot (m\boldsymbol{g}) \\
\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{p})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) \\
\frac{d (\boldsymbol{e}_i \cdot (m\cdot \boldsymbol{v}))}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) \\
m\frac{d (\boldsymbol{e}_i \cdot \boldsymbol{v})}{dt} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) \\
m\frac{d^2 (\boldsymbol{e}_i \cdot \boldsymbol{r})}{{dt}^2} &= m \cdot (\boldsymbol{e}_i \cdot \boldsymbol{g}) \\
\end{align}
\]
ここで、\(\boldsymbol{e}_2\) が \(\boldsymbol{g}\) と平行である (つまり、\(\boldsymbol{g}\) が \(\boldsymbol{e}_1,\boldsymbol{e}_3\) 方向に成分を持たない) とし、さらに
\[
\begin{align}
x(t) &= \boldsymbol{e}_1 \cdot \boldsymbol{r}(t) \\
y(t) &= \boldsymbol{e}_2 \cdot \boldsymbol{r}(t) \\
z(t) &= \boldsymbol{e}_3 \cdot \boldsymbol{r}(t) \\
\end{align}
\]
と置くと、次の各3つの成分に関する方程式が得られる。
\[
\begin{align}
m\frac{d^2 x}{{dt}^2} &= 0 \\
m\frac{d^2 y}{{dt}^2} &= m \cdot (\boldsymbol{e}_2 \cdot \boldsymbol{g}) \\
m\frac{d^2 z}{{dt}^2} &= 0 \\
\end{align}
\]
一応補足しておくと、 \(\boldsymbol{e}_2 \cdot \boldsymbol{g}\) は、
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と同じ向きに設定した場合、\(g\)
- \(\boldsymbol{e}_2\) を \(\boldsymbol{g}\) と逆の向きに設定した場合、\(-g\)
である。
練習問題
例題1: 単純な自由落下

あるリンゴがたくさん実っている木がある。そのリンゴの木の全体の様子を映像として録画しているとふと1つのリンゴが木から落ち始め、その一部始終を偶然カメラに収めることに成功した。
その録画された映像を見直して、そのリンゴが落下を始めた瞬間から地面に着地するまでの秒数を調べてみたところ、それは大体 0.45 秒であった。
さらにそのリンゴが落下するまでの過程において枝や幹等への衝突は一切なく、またその落下の最中には特に目立った強風は吹いていなかったとする。
その録画された映像を見直して、そのリンゴが落下を始めた瞬間から地面に着地するまでの秒数を調べてみたところ、それは大体 0.45 秒であった。
さらにそのリンゴが落下するまでの過程において枝や幹等への衝突は一切なく、またその落下の最中には特に目立った強風は吹いていなかったとする。
この時、その落下したリンゴが実っていた位置から着地点までの距離は大体何メートル程度であったのかを概算せよ。
【解き方の例】
\(\boldsymbol{r}_{0}\) をリンゴの初期位置、
\(\boldsymbol{r}_{c}\) をリンゴの着地点
\(m\) をリンゴの質量
\(d\) を初期位置から着地点までの距離
とする。
\(\boldsymbol{r}_{c}\) をリンゴの着地点
\(m\) をリンゴの質量
\(d\) を初期位置から着地点までの距離
とする。
ここでリンゴの着地点 \(\boldsymbol{r}_{c}\) というのは、初期位置 \(\boldsymbol{r}_{0}\) から「下向き」即ち「重力加速度の方向 \(\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}\)」に距離 \(d\) だけ変位した位置となる。
これを数式を使って表し直せば
これを数式を使って表し直せば
\[
\boldsymbol{r}_{c} = \boldsymbol{r}_{0} + d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
ということである。
いま考えたいのは、途中に障害物はなく風の影響もすべて無視した上での落下距離の概算であるので、リンゴを単なる質量 \(m\) の質点と見做した上での局所重力以外の力をすべて無視した方程式で十分であろう。
(リンゴを半径 \(r\) の球体と見做して、その分を着地点までの距離から差し引くことで少しリアルに近づくのではと思うかもしれないが、今はただの概算なので \(r \ll d\) と考えて、 リンゴの大きさの影響を無視してしまっても大丈夫である。かなり大雑把であることに不満を感じるかもしれないが、その辺は剛体のセクションに入ってからじっくり考えていくので今はこれで我慢してほしい。)
(リンゴを半径 \(r\) の球体と見做して、その分を着地点までの距離から差し引くことで少しリアルに近づくのではと思うかもしれないが、今はただの概算なので \(r \ll d\) と考えて、 リンゴの大きさの影響を無視してしまっても大丈夫である。かなり大雑把であることに不満を感じるかもしれないが、その辺は剛体のセクションに入ってからじっくり考えていくので今はこれで我慢してほしい。)
ということで先ほどの運動方程式を解くと
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt}(t) &= m\boldsymbol{g} \\
m \frac{d \boldsymbol{v}}{dt}(t) &= m\boldsymbol{g} \\
m \frac{d^2 \boldsymbol{r}}{dt^2}(t) &= m\boldsymbol{g} \\
\frac{d^2 \boldsymbol{r}}{dt^2}(t) &= \boldsymbol{g} \\
\frac{d \boldsymbol{r}}{dt}(t) &= \boldsymbol{g} t + \boldsymbol{C}_1 \\
\boldsymbol{r}(t) &= \frac{1}{2}\boldsymbol{g} t^2 + \boldsymbol{C}_1 t + \boldsymbol{C}_2 \\
\end{align}
\]
元々実っていたものが落下し始めたということは、初速が \(\boldsymbol{0}\) であったということである。
このことを踏まえてこの一般解に初期条件を適用していく。
このことを踏まえてこの一般解に初期条件を適用していく。
・初速 \(\boldsymbol{0}\)
\[
\begin{align}
\frac{d^2 \boldsymbol{r}}{dt^2}(0) &= \boldsymbol{0} \\
\boldsymbol{g}\cdot 0 + \boldsymbol{C}_1 &= \boldsymbol{0} \\
\boldsymbol{C}_1 &= \boldsymbol{0} \\
\end{align}
\]
・初期位置 \(\boldsymbol{r}_{0}\)
\[
\begin{align}
\boldsymbol{r}(0) &= \boldsymbol{r}_{0} \\
\frac{1}{2}\boldsymbol{g}\cdot 0^2 + \boldsymbol{C}_1\cdot 0 + \boldsymbol{C}_2 &= \boldsymbol{r}_{0} \\
\boldsymbol{C}_2 &= \boldsymbol{r}_{0} \\
\end{align}
\]
つまり、初期条件を与えた特殊解は
\[
\boldsymbol{r}(t) = \boldsymbol{r}_{0} + \frac{1}{2}\boldsymbol{g} t^2
\]
今問題になっているのは、\(\boldsymbol{r}_{0}\) から \(\boldsymbol{r}_{c}\) までの距離 \(d\) であるが、今持っている関係式は
\[
\boldsymbol{r}_{c} = \boldsymbol{r}_{0} + d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
であり、これだけでは \(d\) について解きようがない。
しかし運動方程式が解けたことによって \(\boldsymbol{r}_{c}\) を既知量である初期位置からそこにたどり着くまでの時間 \(t_c\) を使って次のように表せることに注意しよう。
しかし運動方程式が解けたことによって \(\boldsymbol{r}_{c}\) を既知量である初期位置からそこにたどり着くまでの時間 \(t_c\) を使って次のように表せることに注意しよう。
\[
\boldsymbol{r}(t_c) = \boldsymbol{r}_{c}
\]
つまり
\[
\begin{align}
\boldsymbol{r}(t_c) &= \boldsymbol{r}_{c} \\
\boldsymbol{r}_{0} + \frac{1}{2}\boldsymbol{g} t_c^2 &= \boldsymbol{r}_{0} + d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
\frac{1}{2}\boldsymbol{g} t_c^2 &= d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
(\frac{1}{2}t^2)\cdot(\lVert \boldsymbol{g} \rVert\cdot \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}) &= d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
(\frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2)\cdot \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= d\cdot\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
(\frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2 - d)\cdot \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= \boldsymbol{0} \\
\end{align}
\]
ここで、重力加速度は零ベクトルではない。
つまり
「零ベクトルでない \(\boldsymbol{x}\) が、恒等式 \(a\cdot \boldsymbol{x} = \boldsymbol{0}\) を満たすためには、その係数 \(a\) が恒等的にゼロでなければいけない」
という帰結を使用できる。
つまり
「零ベクトルでない \(\boldsymbol{x}\) が、恒等式 \(a\cdot \boldsymbol{x} = \boldsymbol{0}\) を満たすためには、その係数 \(a\) が恒等的にゼロでなければいけない」
という帰結を使用できる。
即ち
\[
\begin{align}
\frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2 - d &= 0 \\
\frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2 &= d \\
\end{align}
\]
ちなみに、より直観的である
\[
\lVert \boldsymbol{r}_{c} - \boldsymbol{r}_{0} \rVert = d
\]
という式からも
\[
\begin{align}
\lVert \boldsymbol{r}_{c} - \boldsymbol{r}_{0} \rVert &= d \\
\lVert (\boldsymbol{r}_{0} + \frac{1}{2}\boldsymbol{g} t_c^2) - \boldsymbol{r}_{0} \rVert &= d \\
\lVert \frac{1}{2}\boldsymbol{g}\cdot t_c^2 \rVert &= d \\
\left\lvert \frac{1}{2}t_c^2 \right\rvert \cdot \lVert \boldsymbol{g} \rVert &= d \\
\frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2 &= d \\
\end{align}
\]
というように同じ式が得られる。
\(t_c\) は \(0.45[s]\)、\(\lVert \boldsymbol{g} \rVert\) は大体 \(9.8[m/s^2]\) より
\[
\begin{align}
d &= \frac{1}{2}\lVert \boldsymbol{g} \rVert\ t_c^2 \\
&= \frac{1}{2}\cdot (9.8[m/s^2])\cdot (0.45[s])^2 \\
&= \frac{1}{2}\cdot (9.8[m/s^2])\cdot (0.45^2[s^2]) \\
&= \frac{9.8\cdot 0.45^2}{2}[m] \\
&= \frac{9.8\cdot 0.45^2}{2}[m] \\
&= 2.205[m] \\
\end{align}
\]
よって答えは、およそ \(2.2[m]\)
例題2: 少し複雑な放物運動

(要修正)
勾配が34.5°で一定である坂道が300メートルにもわたってずっと一直線に続く場所があるとする。
まずその下り坂の開始地点から大体5メートル程先の適当な一点に立って、その立っている地点に印を付ける。
そしてそこから泥をまぶしたテニスボールを坂道を下る方向に向かって左右方向にぶれないように思いっきり投げた。すると遥か遠方でボールが地面に強く衝突した。
投げた瞬間から着地までの時間をストップウォッチで計ってもらっていた相方さんに結果を聞くと7秒89であった。
加えて飛距離を調べるため、相方と協力してスタート位置の印があった地点とボールが地面に衝突した際に付着した一つ目の泥の跡があった地点の間の距離を測ると51.0メートルであったこともわかった。
その後一応確認のため、ボールの着地地点から左右両側方向に向かってラインを引き、スタート地点にボールをそっと置きそのまま転がっていく先を追跡してみたところ、その引いたラインとの交差位置と、ボールの実際の着地点との間に7.0メートルものブレがあり、実はまっすぐに投げることができず向かって左側方向に軌道が逸れてしまっていたことが最後に判明してしまった。
まずその下り坂の開始地点から大体5メートル程先の適当な一点に立って、その立っている地点に印を付ける。
そしてそこから泥をまぶしたテニスボールを坂道を下る方向に向かって左右方向にぶれないように思いっきり投げた。すると遥か遠方でボールが地面に強く衝突した。
投げた瞬間から着地までの時間をストップウォッチで計ってもらっていた相方さんに結果を聞くと7秒89であった。
加えて飛距離を調べるため、相方と協力してスタート位置の印があった地点とボールが地面に衝突した際に付着した一つ目の泥の跡があった地点の間の距離を測ると51.0メートルであったこともわかった。
その後一応確認のため、ボールの着地地点から左右両側方向に向かってラインを引き、スタート地点にボールをそっと置きそのまま転がっていく先を追跡してみたところ、その引いたラインとの交差位置と、ボールの実際の着地点との間に7.0メートルものブレがあり、実はまっすぐに投げることができず向かって左側方向に軌道が逸れてしまっていたことが最後に判明してしまった。
この時、
(1) 計測を行う場所が坂道ではなく勾配の一切ない真っ平らなグラウンドであった場合、その「ボールを投げた位置から、着地位置までの直線距離」の記録は何メートルになっていたのか、加えてその時の最高到達高度は地上から何メートルになるのかを概算せよ。
(2) ボールが放物運動をしている最中に、ボールと斜面の間の最短距離が最も離れる時のその距離は何メートルなのかを概算せよ。
(1) 計測を行う場所が坂道ではなく勾配の一切ない真っ平らなグラウンドであった場合、その「ボールを投げた位置から、着地位置までの直線距離」の記録は何メートルになっていたのか、加えてその時の最高到達高度は地上から何メートルになるのかを概算せよ。
(2) ボールが放物運動をしている最中に、ボールと斜面の間の最短距離が最も離れる時のその距離は何メートルなのかを概算せよ。
但し、空気抵抗や風、地面の凹凸については全て無視してよいものとする。
【解き方の例】
例題1と比べると複雑に見えるが、ベクトルを存分に活用するという点を除けば、やることはそこまで大それたものではない。
この問題で求めなければならないのは「初速」であるが
例題1と比べると複雑に見えるが、ベクトルを存分に活用するという点を除けば、やることはそこまで大それたものではない。
この問題で求めなければならないのは「初速」であるが
まずこの問題を解く上で必要になってくる方向をベクトルで一通り定義してしまおう。
・下向き
\[
\begin{align}
\hat{\boldsymbol{g}}&:=\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
\end{align}
\]
・坂道の面に対して外側を向く法線ベクトル
\[
\begin{align}
\hat{\boldsymbol{n}} \\
\end{align}
\]
・坂道に対して真っ直ぐの方向
\[
\begin{align}
\hat{\boldsymbol{u}}_1&:=\frac{\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}}}{\lVert \hat{\boldsymbol{g}}+\hat{\boldsymbol{n}} \rVert} \\
\end{align}
\]
・坂道に対して真っ直ぐの方向を進行方向として向いているときの左側方向
\[
\begin{align}
\hat{\boldsymbol{u}}_2&:=\hat{\boldsymbol{n}}\times\hat{\boldsymbol{u}}_1 \\
\end{align}
\]
(なぜこうなるかの説明をここに入れる)
着地地点の位置ベクトル \(\boldsymbol{r}_{c}\) は、投げた位置から着地点までの距離を \(d = 51.0[m]\), 着地地点の左方向へのブレを \(k = 7.0[m]\) と置くと
\[
\begin{align}
\boldsymbol{r}_{c} = \boldsymbol{r}_{0} + \sqrt{d^2-k^2}\cdot\hat{\boldsymbol{u}}_1 + k\cdot\hat{\boldsymbol{u}}_2 \\
\end{align}
\]
である。
\[
\begin{align}
\boldsymbol{r}(t_c) &= \boldsymbol{r}_{c} \\
\boldsymbol{r}_0 + \boldsymbol{v}_0 t_c + \frac{1}{2}\boldsymbol{g} t_c^2 &= \boldsymbol{r}_{0} + \sqrt{d^2-k^2}\cdot\hat{\boldsymbol{u}}_1 + k\cdot\hat{\boldsymbol{u}}_2 \\
\boldsymbol{v}_0 t_c + \frac{1}{2}\boldsymbol{g} t_c^2 &= \sqrt{d^2-k^2}\cdot\hat{\boldsymbol{u}}_1 + k\cdot\hat{\boldsymbol{u}}_2 \\
\boldsymbol{v}_0 &= \frac{(\sqrt{d^2-k^2}\cdot\hat{\boldsymbol{u}}_1 + k\cdot\hat{\boldsymbol{u}}_2)-\frac{1}{2}\boldsymbol{g} t_c^2}{t_c} \\
\end{align}
\]
分母の第一項に注目すると
\[
\begin{align}
& \sqrt{d^2-k^2}\cdot\hat{\boldsymbol{u}}_1 + k\cdot\hat{\boldsymbol{u}}_2 \\
=& \sqrt{d^2-k^2}\cdot\frac{\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}}}{\lVert \hat{\boldsymbol{g}}+\hat{\boldsymbol{n}} \rVert} + k\cdot\hat{\boldsymbol{n}}\times(\frac{\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}}}{\lVert \hat{\boldsymbol{g}}+\hat{\boldsymbol{n}} \rVert}) \\
=& \frac{1}{\lVert \hat{\boldsymbol{g}}+\hat{\boldsymbol{n}} \rVert}(\sqrt{d^2-k^2}\cdot(\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}}) + k\cdot\hat{\boldsymbol{n}}\times\hat{\boldsymbol{g}}) \\
\end{align}
\]
勾配がないと考えたとき、最高高度となるのは速度の重力加速度方向成分が 0 になる瞬間なので
\[
\begin{align}
\hat{\boldsymbol{g}}\cdot\frac{d \boldsymbol{r}}{dt}(t_p) &= 0 \\
\hat{\boldsymbol{g}}\cdot({\boldsymbol{v}_0 + \boldsymbol{g} t_p})&= 0 \\
\hat{\boldsymbol{g}}\cdot({\boldsymbol{v}_0 + \boldsymbol{g} t_p})&= 0 \\
\end{align}
\]
上向き \(-\hat{\boldsymbol{g}}\) と 面の外向き法線 \(\hat{\boldsymbol{n}}\) のなす角は34.5°より、 \(\theta=34.5\times\frac{\pi}{180}\) と置くと
\[
\begin{align}
(-\hat{\boldsymbol{g}})\cdot\hat{\boldsymbol{n}} &= \lVert -\hat{\boldsymbol{g}} \rVert \cdot \lVert \hat{\boldsymbol{n}} \rVert \cos(\theta) \\
-(\hat{\boldsymbol{g}}\cdot\hat{\boldsymbol{n}}) &= \cos(\theta) \\
\hat{\boldsymbol{g}}\cdot\hat{\boldsymbol{n}} &= -\cos(\theta) \\
\end{align}
\]
であり、ベクトル \(\hat{\boldsymbol{n}}\) 自体は漠然と与えられていたものであるにもかかわらず、坂道の勾配が具体的に与えられていることによって、このようにそのベクトルと重力加速度方向との内積に限っては問題なく計算できることになる。
\[
\begin{align}
& \lVert \hat{\boldsymbol{g}}+\hat{\boldsymbol{n}} \rVert \\
=& \sqrt{(\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}})\cdot(\hat{\boldsymbol{g}}+\hat{\boldsymbol{n}})} \\
=& \sqrt{{\lVert \hat{\boldsymbol{g}} \rVert}^2 + 2(\hat{\boldsymbol{g}}\cdot\hat{\boldsymbol{n}})+ {\lVert \hat{\boldsymbol{n}} \rVert}^2} \\
=& \sqrt{1+2(\hat{\boldsymbol{g}}\cdot\hat{\boldsymbol{n}})+1} \\
=& \sqrt{2\cdot(1+\hat{\boldsymbol{g}}\cdot\hat{\boldsymbol{n}})} \\
\end{align}
\]
であるので、一見計算できなそうなそれらの和の大きさというのも、それらの内積がわかれば計算できてしまう。
\(t_p\) について解くと、大体 \(3.7512584160819\) 秒という値になる。
この値を運動方程式の解に代入することで、最高高度に達した時の位置ベクトルが求まり、初期位置からその位置までの変位ベクトルを重力加速度方向への射影ともう一つのベクトルに分解すれば答えが得られる。
タグ一覧:
