雑記帳
一端が固定されたバネに繋がれた物体の運動
運動方程式 (EOM: Equation Of Motion)
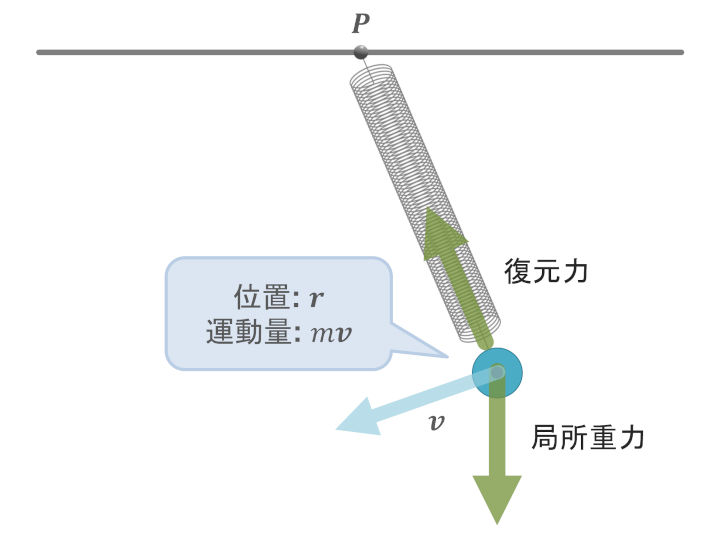
一般形
方程式の全容
(理想化された) バネで繋がれた物体の運動方程式は、
- \(m\): 物体の質量
- \(\boldsymbol{r}\): 物体の位置
- \(l_0\): バネの自然長 (\(l_0 > 0\))
- \(k\): バネ定数 (\(k > 0\))
- \(\boldsymbol{P}\): 固定点の位置
としたとき、以下で表すことができる。
\[
\frac{d \boldsymbol{p}}{dt} = m\boldsymbol{g} + k\cdot(\lVert \boldsymbol{P} - \boldsymbol{r} \rVert - l_0)\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}
\]
この方程式は非線形方程式であり解析的に解くことが困難であるが、上の図から察しがつくように、この方程式に従う運動は基本的に「バネ振り子」のそれであり、大体の運動のイメージはつけられる。
方程式の立て方
まず図を見ての通り、物体に作用する力として考えるのは以下の2つとなる。
- 局所重力 \(\boldsymbol{F}_1\)
- 復元力 (弾性力とも呼ばれる) \(\boldsymbol{F}_2\)
局所重力 \(\boldsymbol{F}_1\) はいつも通り
\[
\boldsymbol{F}_1 = m\boldsymbol{g}
\]
である。
続いて、復元力 \(\boldsymbol{F}_2\) だが、これは空気抵抗を考えたときと同様、「力の大きさ」と「力の方向」に分けて考えるのが簡単である。
まず力の大きさ \(\lVert \boldsymbol{F}_2 \rVert\) は以下のように考える。
時間 \(t\) におけるバネの長さ \(l(t)\) というのは
\[
l(t) = \lVert \boldsymbol{r} - \boldsymbol{P} \rVert
\]
より、(符号付きの) バネの伸び \(\Delta l\) は
\[
\Delta l = l(t) - l_0
\]
として表せるわけである。
バネの復元力の大きさは、バネの伸びに比例するわけだから比例係数となるバネ定数を \(k\) (\(k>0\)) とすると、
\[
\begin{align}
\lVert \boldsymbol{F}_2 \rVert &= k\cdot \lvert \Delta l \rvert \\
&= k\cdot \lvert l(t) - l_0 \rvert \\
&= k\cdot \lvert \lVert \boldsymbol{r} - \boldsymbol{P} \rVert - l_0 \rvert \\
&= k\cdot \lvert \lVert \boldsymbol{P} - \boldsymbol{r} \rVert - l_0 \rvert \\
\end{align}
\]
となる。
一方で力の単位方向ベクトル \(\hat{\boldsymbol{F}_2}\) は、図を見てのとおり、
■ バネが伸びているとき (\(\Delta l \ge 0\))
「位置 \(\boldsymbol{r}\) を基点に位置 \(\boldsymbol{P}\) を向く方向 \((\boldsymbol{P} - \boldsymbol{r})\)」を規格化した単位ベクトル \(\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\)
「位置 \(\boldsymbol{r}\) を基点に位置 \(\boldsymbol{P}\) を向く方向 \((\boldsymbol{P} - \boldsymbol{r})\)」を規格化した単位ベクトル \(\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\)
■ バネが縮んでいるとき (\(\Delta l < 0\))
「位置 \(\boldsymbol{r}\) を基点に \(\boldsymbol{P}\) を向く方向 \((\boldsymbol{P} - \boldsymbol{r})\)」を規格化した単位ベクトル \(\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\) と真逆の向き \(-\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\)
「位置 \(\boldsymbol{r}\) を基点に \(\boldsymbol{P}\) を向く方向 \((\boldsymbol{P} - \boldsymbol{r})\)」を規格化した単位ベクトル \(\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\) と真逆の向き \(-\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert}\)
「力の方向」と「力の大きさ」が求まれば
\[
\boldsymbol{F}_2 = \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2}
\]
より、\(\boldsymbol{F}_2\) は
■ バネが伸びているとき (\(\Delta l \ge 0\))
\[
\begin{align}
\boldsymbol{F}_2 &= \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2} \\
&= \left( k\cdot \lvert \Delta l \rvert \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
\end{align}
\]
■ バネが縮んでいるとき (\(\Delta l < 0\))
\[
\begin{align}
\boldsymbol{F}_2 &= \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2} \\
&= \left( k\cdot \lvert \Delta l \rvert \right) \cdot \left( -\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
\end{align}
\]
であるが、絶対値を外してみると、それらの式は同じ
\[
\boldsymbol{F}_2 = \left( k\cdot \Delta l \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right)
\]
一本の式で書けることに気づく。
■ バネが伸びているとき (\(\Delta l \ge 0\))
\[
\begin{align}
\boldsymbol{F}_2 &= \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2} \\
&= \left( k\cdot \lvert \Delta l \rvert \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
&= \left( k\cdot \Delta l \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
\end{align}
\]
■ バネが縮んでいるとき (\(\Delta l < 0\))
\[
\begin{align}
\boldsymbol{F}_2 &= \lVert \boldsymbol{F}_2 \rVert \cdot \hat{\boldsymbol{F}_2} \\
&= \left( k\cdot \lvert \Delta l \rvert \right) \cdot \left( -\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
&= \left( -k\cdot \Delta l \right) \cdot \left( -\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
&= \left( k\cdot \Delta l \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
\end{align}
\]
以上を纏めると
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt} &= m\boldsymbol{g} + \left( k\cdot \Delta l \right) \cdot \left( \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \right) \\
&= m\boldsymbol{g} + \left( k\cdot (\lVert \boldsymbol{P} - \boldsymbol{r} \rVert - l_0) \right) \frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \\
\end{align}
\]
つまり、冒頭に与えた方程式を得ることができた。
特定の条件が課された状況下での運動方程式
単振動
「復元力が重力加速度方向以外の成分を持たないケース」、つまりは「単振動」の場合に条件を絞れば、運動方程式は非常に単純になる。
まず仮定より、運動 \(\boldsymbol{r}(t)\) は、ある関数 \(\alpha(t)\) があって
\[
\boldsymbol{r}(t) = \boldsymbol{P} + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
という形で書かれることになる。
ここで、\(\alpha(t)\) は、「時間 \(t\) におけるバネの長さ」として考えるため、\(\alpha(t) > 0\) (バネの長さが 0 にはならない) という条件を課しておく。
まず上の式を運動方程式に代入してみると次のようになる
\[
\begin{align}
\frac{d \boldsymbol{p}}{dt} &= m\boldsymbol{g} + k\cdot(\lVert \boldsymbol{P} - \boldsymbol{r} \rVert - l_0)\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \\
m\frac{d^2 \boldsymbol{r}}{dt^2} &= m\boldsymbol{g} + k\cdot(\lVert \boldsymbol{P} - \boldsymbol{r} \rVert - l_0)\frac{\boldsymbol{P} - \boldsymbol{r}}{\lVert \boldsymbol{P} - \boldsymbol{r} \rVert} \\
\boldsymbol{0} + m\frac{d^2 \alpha}{dt^2}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\boldsymbol{g} + k\cdot(\lvert \alpha(t) \rvert - l_0)\frac{-\alpha(t)}{\lvert \alpha(t) \rvert}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
\end{align}
\]
\(\alpha(t) > 0\) より
\[
\begin{align}
\boldsymbol{0} + m\frac{d^2 \alpha}{dt^2}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\boldsymbol{g} + k\cdot(\lvert \alpha(t) \rvert - l_0)\frac{-\alpha(t)}{\lvert \alpha(t) \rvert}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
m\frac{d^2 \alpha}{dt^2}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} &= m\boldsymbol{g} + k\cdot(\alpha(t) - l_0)\frac{-\alpha(t)}{\alpha(t)}\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
\boldsymbol{0} &= \left( m\frac{d^2 \alpha}{dt^2} - (m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha(t) - l_0)) \right) \frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert} \\
0 &= m\frac{d^2 \alpha}{dt^2} - (m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha(t) - l_0)) \\
m\frac{d^2 \alpha}{dt^2}(t) &= m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha(t) - l_0) \\
\end{align}
\]
つまり \(\alpha\) が満たすべき方程式として次の方程式が得られる。
\[
m\frac{d^2 \alpha}{dt^2} = m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha - l_0)
\]
練習問題
例1: バネで吊るされた物体の直線的な往復運動 (単振動)
一般解を求める
バネでつるされた重力加速度方向のみ往復運動をする物体の運動方程式は、先ほど求めた通り
\[
\boldsymbol{r}(t) = \boldsymbol{P} + \alpha(t)\frac{\boldsymbol{g}}{\lVert \boldsymbol{g} \rVert}
\]
というバネの長さ \(\alpha(t)>0\) に関する方程式
\[
m\frac{d^2 \alpha}{dt^2} = m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha - l_0)
\]
として記述できる。
この方程式の一般解を求めるのは簡単で
\[
\begin{align}
m\frac{d^2 \alpha}{dt^2} &= m\lVert \boldsymbol{g} \rVert - k\cdot (\alpha - l_0) \\
m\frac{d^2 \alpha}{dt^2} &= -k \cdot (\alpha - l_0 - \frac{mg}{k}) \\
\frac{d^2 \alpha}{dt^2} &= -\frac{k}{m} \cdot (\alpha - (l_0 + \frac{mg}{k})) \\
\end{align}
\]
ここで
\[
\begin{align}
\omega^2 &:= \frac{k}{m} \\
A(t) &:= \alpha(t) - (l_0 + \frac{mg}{k}) \\
\end{align}
\]
と置くと
\[
\begin{align}
\frac{d^2 \alpha}{dt^2} &= -\frac{k}{m} \cdot (\alpha - (l_0 + \frac{mg}{k})) \\
\frac{d^2 A}{dt^2} + 0 &= -\omega^2 A \\
\frac{d^2 A}{dt^2}(t) &= -\omega^2 A(t) \\
A(t) &= C_{+} e^{i\omega t} + C_{-} e^{-i\omega t} \\
\alpha(t) - (l_0 + \frac{mg}{k}) &= C_{+} e^{i\sqrt{\frac{k}{m}} t} + C_{-} e^{-i\sqrt{\frac{k}{m}} t} \\
\alpha(t) &= (l_0 + \frac{mg}{k}) + C_{+} e^{i\sqrt{\frac{k}{m}} t} + C_{-} e^{-i\sqrt{\frac{k}{m}} t} \\
\end{align}
\]
初期条件を具体的に適用する
一応一般解は求まったが、この複素数の範囲での解ではどういった運動であるのかのイメージが付きづらいかもしれないので、ここから具体的に初期条件を適用して、イメージしやすい実数解の形へと持っていってみる。
ここでは次の初期条件を一般解に適用する。
\[
\begin{align}
\alpha(0) &= l_0 \\
\frac{d \alpha}{dt}(0) &= 0 \\
\end{align}
\]
意味合いとしては見ての通り
- バネが自然長にある状態から、自由落下の要領でそっと運動を開始させる
ということである。
では実際に適用していく。
まず一般解
\[
\alpha(t) = (l_0 + \frac{mg}{k}) + C_{+} e^{i\omega t} + C_{-} e^{-i\omega t}
\]
に一つ目の条件を適用すると
\[
\begin{align}
\alpha(0) &= (l_0 + \frac{mg}{k}) + C_{+} e^{i\omega 0} + C_{-} e^{-i\omega 0} \\
l_0 &= (l_0 + \frac{mg}{k}) + C_{+} + C_{-} \\
C_{+} + C_{-} &= -\frac{mg}{k} \\
\end{align}
\]
となる。
続いて速度の式
\[
\frac{d \alpha}{dt}(t) = i\omega C_{+} e^{i\omega t} -i\omega C_{-} e^{-i\omega t}
\]
に2つ目の条件を適用すると
\[
\begin{align}
\frac{d \alpha}{dt}(0) &= i\omega C_{+} e^{i\omega 0} -i\omega C_{-} e^{-i\omega 0} \\
0 &= i\omega C_{+} -i\omega C_{-} \\
0 &= i\omega \cdot (C_{+} - C_{-}) \\
\end{align}
\]
\(\omega > 0\) より
\[
\begin{align}
0 &= i\omega \cdot (C_{+} - C_{-}) \\
0 &= C_{+} - C_{-} \\
C_{+} &= C_{-} \\
\end{align}
\]
ここで、\(C:=C_{+}\) とすると
\[
\begin{align}
C_{+} + C_{-} &= -\frac{mg}{k} \\
C + C &= -\frac{mg}{k} \\
C &= -\frac{mg}{2k} \\
\end{align}
\]
というように、任意定数が具体的に定まった。
これを一般解に代入すると
\[
\begin{align}
\alpha(t) &= (l_0 + \frac{mg}{k}) + C_{+} e^{i\omega t} + C_{-} e^{-i\omega t} \\
&= (l_0 + \frac{mg}{k}) + C e^{i\omega t} + C e^{-i\omega t} \\
&= (l_0 + \frac{mg}{k}) -\frac{mg}{2k} ( e^{i\omega t} + e^{-i\omega t}) \\
&= (l_0 + \frac{mg}{k}) -\frac{mg}{2k} (2\cdot \frac{e^{i\omega t} + e^{-i\omega t}}{2}) \\
&= (l_0 + \frac{mg}{k}) -\frac{mg}{k} \cos(\omega t) \\
&= (l_0 + \frac{mg}{k}) -\frac{mg}{k} \cos(\sqrt{\frac{k}{m}} t) \\
\end{align}
\]
文字に数値を代入して具体的な値を求めてみる
先ほど初期条件を与えることで得た具体的な一つの実数解に対して、実際に数字を代入して運動の様子を具体的に可視化してみる。
- \(m = 0.1[{\rm kg}]\)
- \(l_0 = 0.15[{\rm m}]\)
- \(k = 11[{\rm N}/{\rm m}]\)
として具体的な運動の関数を求めてみると
\[
\begin{align}
\alpha(t) &= (l_0 + \frac{mg}{k}) -\frac{mg}{k} \cos(\sqrt{\frac{k}{m}} t) \\
&= (0.15[{\rm m}] + \frac{0.1[{\rm kg}] \times 9.8[{\rm m}/{\rm s}^2]}{11[{\rm N}/{\rm m}]}) -\frac{0.1[{\rm kg}] \times 9.8[{\rm m}/{\rm s}^2]}{11[{\rm N}/{\rm m}]} \cos(\sqrt{\frac{11[{\rm N}/{\rm m}]}{0.1[{\rm kg}]}} \times t) \\
&= (0.15[{\rm m}] + \frac{49}{550}[{\rm m}]) - \frac{49}{550}[{\rm m}] \cos(\sqrt{110[{\rm s}^{-2}]} \times t) \\
&= \frac{263}{1100}[{\rm m}] - \frac{49}{550}[{\rm m}] \cos(\sqrt{110}[{\rm s}^{-1}] \times t) \\
\end{align}
\]
となる。
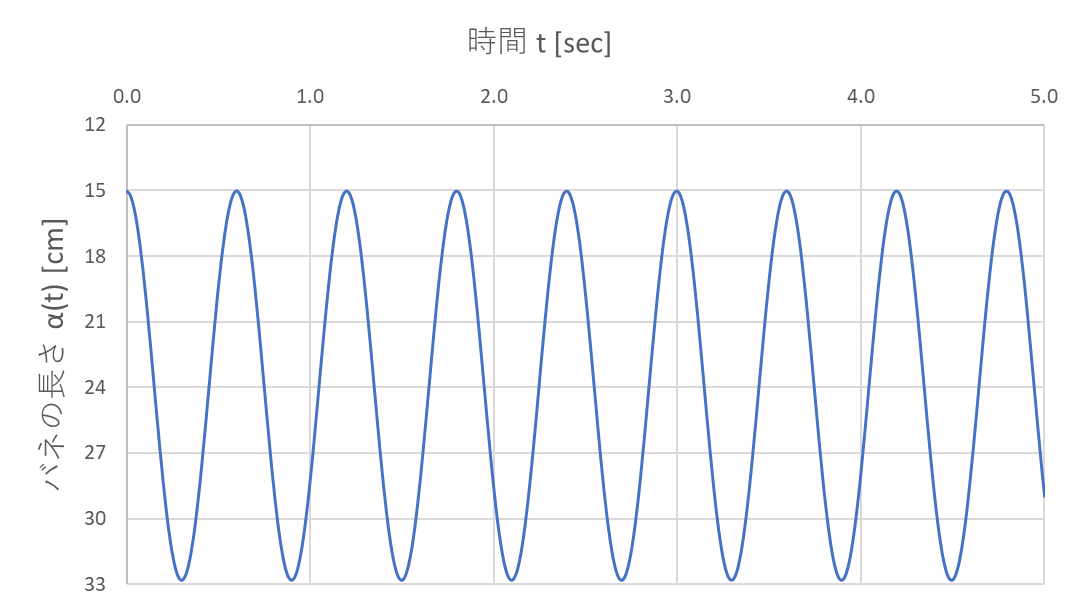
例えば、2秒後のバネの長さは上の式を用いて
\[
\begin{align}
\alpha(2[{\rm s}]) &= \frac{263}{1100}[{\rm m}] - \frac{49}{550}[{\rm m}] \cos(\sqrt{110}[{\rm s}^{-1}] \times 2[{\rm s}]) \\
&= \frac{263}{1100}[{\rm m}] - \frac{49}{550}[{\rm m}] \cos(2\sqrt{110}) \\
&\simeq 0.286099197 [{\rm m}] \\
&\simeq 28.61 [{\rm cm}] \\
\end{align}
\]
というように具体的な数値として求まる。
おまけとして、5秒後までのバネの長さの時間変化をグラフにした図を以下に載せておく。
タグ一覧:
