雑記帳
バネで繋がれたn個の物体の運動方程式とその境界条件の考え方
運動方程式 (EOM: Equation Of Motion)
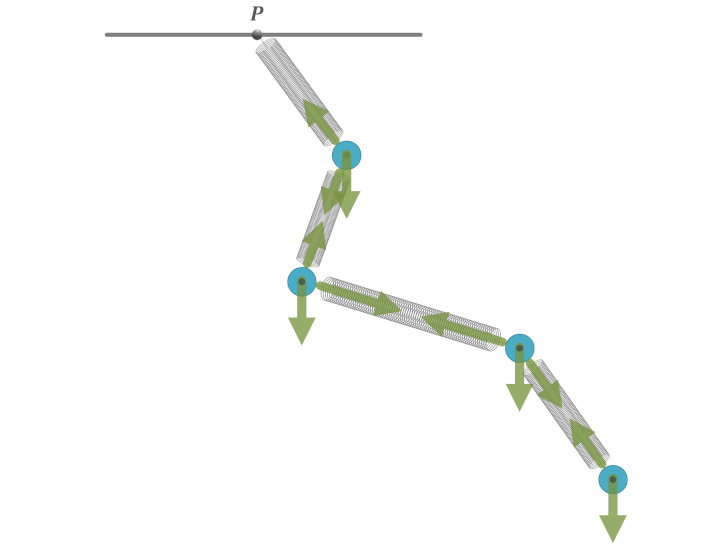
一般形
方程式の全容
(理想化された) バネで繋がれたN個の物体の運動方程式は、\(n = 1,2,..,N\) に対して
- \(m_n\): n番目の物体の質量
- \(\boldsymbol{r}_n\): n番目の物体の位置
- \(l_{n,n+1}\): n番目と(n+1)番目の物体を繋ぐバネの自然長 (\(l_{n,n+1} > 0\))
- \(k_{n,n+1}\): n番目と(n+1)番目の物体を繋ぐバネのバネ定数 (\(k_{n,n+1} > 0\))
- \(\boldsymbol{r}_0, \boldsymbol{r}_{N+1}\): (実在している必要のない) 仮想的な質点の位置
- \(l_{0,1}, l_{N,N+1}\): (実在している必要のない) 仮想的なバネの自然長
- \(k_{0,1}, k_{N,N+1}\): (実在している必要のない) 仮想的なバネのバネ定数
としたとき、以下で表すことができる。
\[
\frac{d \boldsymbol{p}_n}{dt} = m_n\boldsymbol{g} + k_{n-1,n}\cdot(\lVert \boldsymbol{r}_{n-1} - \boldsymbol{r}_n \rVert - l_{n-1,n})\frac{\boldsymbol{r}_{n-1} - \boldsymbol{r}_n}{\lVert \boldsymbol{r}_{n-1} - \boldsymbol{r}_n \rVert} + k_{n,n+1}\cdot(\lVert \boldsymbol{r}_{n+1} - \boldsymbol{r}_n \rVert - l_{n,n+1})\frac{\boldsymbol{r}_{n+1} - \boldsymbol{r}_n}{\lVert \boldsymbol{r}_{n+1} - \boldsymbol{r}_n \rVert}
\]
また上は、「バネで繋がれる物体の数は、1つの物体につき最大2つ」であるようなものに対する方程式であるが、「バネで繋がれる物体の数が3つ以上になっている箇所がある」といった場合になっても、その箇所に復元力の項が加わるだけで、運動方程式の組み立て方は基本的に変わらない。(但し、格子状のような規則性のあるものであれば話は変わるが、そうなった場合基本的には上のようなシンプルな一般式で書くことは難しくなる。)

境界条件
運動方程式を見ての通り、1番目と N番目の物体の運動方程式の中には \(\boldsymbol{r}_0\) や \(\boldsymbol{r}_{N+1}\) といった奇妙な量が含まれるが、これらのとるべき値を上手く設定することによって、両端の物体の在り方を規定することができる。
固定端
一つのパターンは、固定端と呼ばれる
- 端に位置する物体が、位置の固定された何かとバネで繋がれている
という状況である。
「天井に吊るされている」というのがまさにその一例となる。
この状況を表すのは簡単で、\(\boldsymbol{P}\) を固定されたものの位置としたとき
\[
\boldsymbol{r}_0 = \boldsymbol{P}
\]
や
\[
\boldsymbol{r}_{N+1} = \boldsymbol{P}
\]
と設定すればよい。
因みにこの固定端の場合、\(l_{0,1}\) や \(k_{0,1}\) はちゃんと実在するバネに対する自然長やバネ定数ということになる。
自由端
もう一つのパターンとして、自由端と呼ばれる
- 端に位置する物体が、片側のみバネで繋がれている
という状況がある。
この場合、少しトリッキーになるのだが、要するに
- 仮想的なバネから受ける復元力が常に \(\boldsymbol{0}\)
という状況を無理やり作ってしまえばよい。
具体的には、1番目の方程式を例に考えると、まず方程式の中で仮想的なバネから受ける力は以下のフェードアウトさせていない項となる。
\[
\style{color:#DCE7F3}{\frac{d \boldsymbol{p}_1}{dt} = m_1\boldsymbol{g}} + k_{0,1}\cdot(\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1})\frac{\boldsymbol{r}_{1-1} - \boldsymbol{r}_1}{\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert} \style{color:#DCE7F3}{+ k_{1,2}\cdot(\lVert \boldsymbol{r}_{2} - \boldsymbol{r}_1 \rVert - l_{1,2})\frac{\boldsymbol{r}_{12} - \boldsymbol{r}_1}{\lVert \boldsymbol{r}_{2} - \boldsymbol{r}_1 \rVert}}
\]
この項が恒等的に \(\boldsymbol{0}\) になるための条件を調べていく。
\[
\begin{align}
k_{0,1}\cdot(\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1})\frac{\boldsymbol{r}_{1-1} - \boldsymbol{r}_1}{\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert} &= \boldsymbol{0} \\
\end{align}
\]
\(\boldsymbol{r}_{0} \ne \boldsymbol{r}_1\) とすると、
\[
\begin{align}
k_{0,1}\cdot(\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1})\frac{\boldsymbol{r}_{1-1} - \boldsymbol{r}_1}{\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert} &= \boldsymbol{0} \\
k_{0,1}\cdot(\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1}) &= 0 \\
\end{align}
\]
\(k_{0,1} \ne 0\)
\[
\begin{align}
k_{0,1}\cdot(\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1}) &= 0 \\
\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert - l_{0,1} &= 0 \\
\lVert \boldsymbol{r}_{0} - \boldsymbol{r}_1 \rVert &= l_{0,1} \\
\lVert \boldsymbol{r}_1 - \boldsymbol{r}_0 \rVert &= l_{0,1} \\
\end{align}
\]
つまり、
- \(\boldsymbol{r}_0(t)\) が常に \(\boldsymbol{r}_1(t)\) を中心とする半径 \(l_{0,1}\) の球面上の任意の点に居続ける
という設定にすれば、その端は自由端として振舞うことができる。
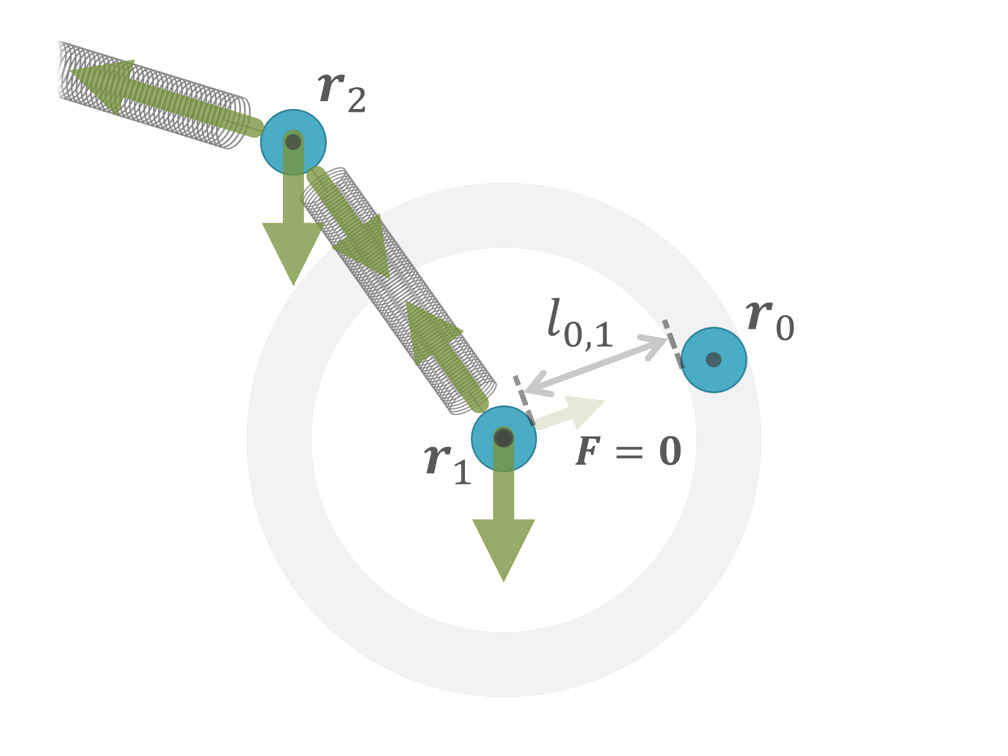
因みにこの自由端の場合、\(l_{0,1}\) や \(k_{0,1}\) は実在しない仮想的なバネに対する便宜的なパラメータということになる。
(ベクトルを積極的に用いない流儀で考える場合、このような自由端の設定方法は少し見慣れないものに感じるかもしれないが、後述する「同じバネで一直線上につながれた物体の連成振動」のセクションを見れば、これがどのようにして見慣れた自由端の設定に行きつくのかを確認することができる。)
特定の条件が課された状況下での運動方程式
同じバネで一直線上につながれた物体の連成振動
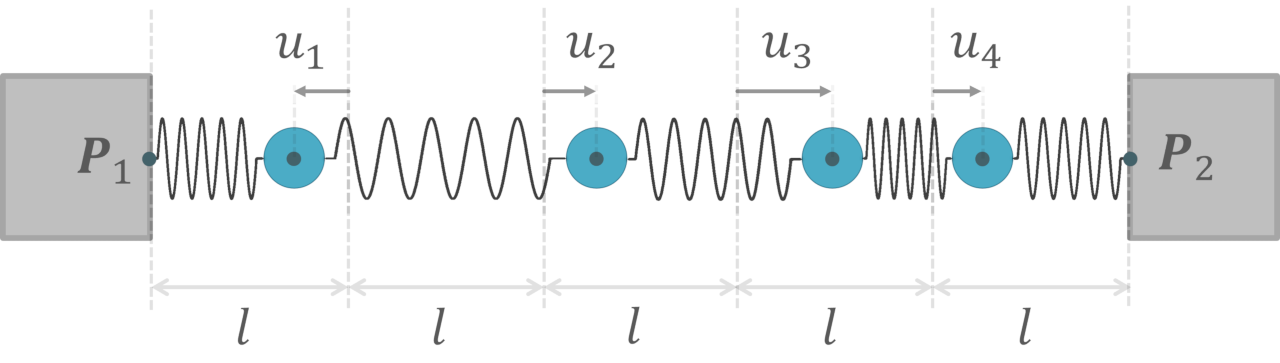
上の式に以下の条件を課す
・局所重力を無視する。
・全てのバネの自然長 \(l_{n,n+1}\) が一定 \(l\) である。
・全てのバネ定数 \(k_{n,n+1}\) が一定 \(k\) である。
・\(\lVert \boldsymbol{P}_2 - \boldsymbol{P}_1 \rVert = (N+1)\cdot l\) を満たすような空間内の2点 \(\boldsymbol{P}_1,\boldsymbol{P}_2\) が与えられている。
・全ての物体の初期位置は、\(\boldsymbol{P}_1\) と \(\boldsymbol{P}_2\) の2点を通る直線上に位置している。
・物体同士の交差は一切起こらない。つまり
・局所重力を無視する。
・全てのバネの自然長 \(l_{n,n+1}\) が一定 \(l\) である。
・全てのバネ定数 \(k_{n,n+1}\) が一定 \(k\) である。
・\(\lVert \boldsymbol{P}_2 - \boldsymbol{P}_1 \rVert = (N+1)\cdot l\) を満たすような空間内の2点 \(\boldsymbol{P}_1,\boldsymbol{P}_2\) が与えられている。
・全ての物体の初期位置は、\(\boldsymbol{P}_1\) と \(\boldsymbol{P}_2\) の2点を通る直線上に位置している。
・物体同士の交差は一切起こらない。つまり
\[
\frac{\boldsymbol{P}_2-\boldsymbol{P}_1}{\lVert \boldsymbol{P}_2-\boldsymbol{P}_1 \rVert}\cdot(\boldsymbol{r}_{n+1}-\boldsymbol{r}_n) > 0
\]
(..)
タグ一覧:
