雑記帳
局所的に射を束ねて得られる対象 【指数対象 (Exponential object)】
(書きかけ)
指数対象 (exponential object)
導入
二項演算 \(f:A\times B \rightarrow C\) と A の大域要素 \(a:1\rightarrow A\) が与えられたとする。
この時、その二項演算の片側の入力を固定値 a で埋めると次のような BとCを結ぶ射
この時、その二項演算の片側の入力を固定値 a で埋めると次のような BとCを結ぶ射
\[
\langle ! {\sf \, ⨟ \,} a , B \rangle {\sf \, ⨟ \,} f
\]
が得られる。
(..)
圏論を既にかじっている人向けに注意をしておくと、そのような対象は「ホム集合」とは異なる。
現在の一階述語論理による公理化として与えている圏という構造の中にそもそも「ホム集合」という概念は存在しない。
(ホモトピー型理論での圏の定義の中には含まれているが、その場合も同様にそのホム集合というのは「考えている圏の対象」にはならない)
現在の一階述語論理による公理化として与えている圏という構造の中にそもそも「ホム集合」という概念は存在しない。
(ホモトピー型理論での圏の定義の中には含まれているが、その場合も同様にそのホム集合というのは「考えている圏の対象」にはならない)
まず「指数対象」がどういった特別なプロセスを伴う対象であるのか
(任意の二項演算に対して片側の入力だけを先行して埋めたプロセスを出力することができるような環境が整備されていると仮定した場合、その出力先となる対象は「プロセスを要素に持つ対象」として考えてよいだろう。この点に着眼し「射を要素に持つ対象」である「指数対象」のあるべき形を定義づける。)
・「射を要素に持つ対象」とはいっても、「対象の要素」である以上は圏の射それ自体とは異なるフォーマットで与えられることになる。(その要素に対して、圏の持つ合成演算を直接適用できない) つまり、「その指数対象の要素を実際の射として評価するためのプロセス \({\rm ev}\) が必要になる。」
(任意の二項演算に対して片側の入力だけを先行して埋めたプロセスを出力することができるような環境が整備されていると仮定した場合、その出力先となる対象は「プロセスを要素に持つ対象」として考えてよいだろう。この点に着眼し「射を要素に持つ対象」である「指数対象」のあるべき形を定義づける。)
・「射を要素に持つ対象」とはいっても、「対象の要素」である以上は圏の射それ自体とは異なるフォーマットで与えられることになる。(その要素に対して、圏の持つ合成演算を直接適用できない) つまり、「その指数対象の要素を実際の射として評価するためのプロセス \({\rm ev}\) が必要になる。」
■ 評価射 \({\rm ev}\) の定義に行きつくまで
二項演算\(f:A\times B \rightarrow C\) について、
・A の一般化要素だけを入力にとり、Xの一般化要素を出力するとある射 \(g:A\rightarrow X\) が存在する。
・Xの一般化要素 \(x=a {\sf \, ⨟ \,} g\) と Bの一般化要素 b が与えられたときに定まるBの一般化要素 \(\langle x,b \rangle {\sf \, ⨟ \,} {\rm ev}\) は \(\langle a,b \rangle {\sf \, ⨟ \,} f\) と等しい。
・上の言明から一般化要素を括りだすと、
二項演算\(f:A\times B \rightarrow C\) について、
・A の一般化要素だけを入力にとり、Xの一般化要素を出力するとある射 \(g:A\rightarrow X\) が存在する。
・Xの一般化要素 \(x=a {\sf \, ⨟ \,} g\) と Bの一般化要素 b が与えられたときに定まるBの一般化要素 \(\langle x,b \rangle {\sf \, ⨟ \,} {\rm ev}\) は \(\langle a,b \rangle {\sf \, ⨟ \,} f\) と等しい。
・上の言明から一般化要素を括りだすと、
\[
\begin{align}
\langle x,b \rangle {\sf \, ⨟ \,} {\rm ev} &= \langle a,b \rangle {\sf \, ⨟ \,} f \\
\langle a {\sf \, ⨟ \,} g,b \rangle {\sf \, ⨟ \,} {\rm ev} &= \langle a,b \rangle {\sf \, ⨟ \,} f \\
\langle a {\sf \, ⨟ \,} g,b {\sf \, ⨟ \,} B \rangle {\sf \, ⨟ \,} {\rm ev} &= \langle a,b \rangle {\sf \, ⨟ \,} f \\
\langle a,b \rangle {\sf \, ⨟ \,} (g \times B) {\sf \, ⨟ \,} {\rm ev} &= \langle a,b \rangle {\sf \, ⨟ \,} f \\
\langle a,b \rangle {\sf \, ⨟ \,} ((g \times B) {\sf \, ⨟ \,} {\rm ev}) &= \langle a,b \rangle {\sf \, ⨟ \,} f \\
\end{align}
\]
となり、少なくとも次の関係式
\[
(g \times B) {\sf \, ⨟ \,} {\rm ev} = f
\]
が満たされていれば先ほどの言明が任意の一般化要素に対して正しいことになる。(一般化要素を括りだした等式からそれら2つの射が等しいことを演繹的に導いているわけではない。そもそもそんなことは一般にできない。ただ単に、括りだされて残った抽象的な射同士が仮に射として等しいければそれら2つの射の出力は入力によらず恒等的に等しくなるということで、それを \({\rm ev}\) の定義に使用してしまおうという) 可換図式で表すと以下のようになる。
・「任意のfについて、上の図式を可換にするような g が一意的に存在する」というように一意性を加えることでいつも通り、ターゲットの空間に余計な情報が入り込まないようにする。
定義
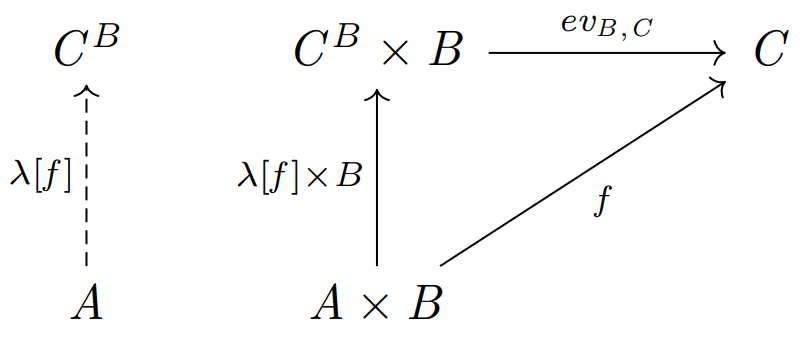
(..)
(積対象からの射が必ずしも「二項演算」に相応しいのか否かは考えている数学的構造に依存し、上の定義だと都合の悪い構造も実際に存在する。その辺の問題を考慮したより適切な「射を要素に持つ対象」の定義付けは存在することには存在するのだが、モノイダル圏の概念が必要になるため一階述語論理を使用して圏論を議論している現段階では扱わない。)
一階の言語による定義
指数対象 \(C^B\) とそれに付随する評価射 \({\rm ev}:C^B \times B \rightarrow B\) は、それぞれ以下を満たす射 \(E,e\) として全て同時に定義される。
\[
{\rm isEvalArr}(e,E,B,C) :\Leftrightarrow \forall X1 \forall p1 \forall q1 \forall A [{\rm arePrj}(p1,q1,X1,A,B) \Rightarrow \forall f [(f:X\rightarrow C) \Rightarrow \exists ! h[ \forall p2 \forall q2 [h:A\rightarrow E \wedge {\rm arePrj}(p2,q2,X2,E,B)) \Rightarrow \exists t1 \exists t2 \exists t3[{\rm \_comp}(p1,h,t1) \wedge {\rm \_comp}(q2,B,t2) \wedge {\rm isParing}(t3,t1,t2,p2,q2,X2,E,B) \wedge {\rm \_comp}(t3,e,f)]]]]]
\]
また指数対象 \(C^B\) は見ての通り評価射と同時に副次的に定義されるため、与えられた対象 \(X\) が \(B\) から \(C\) の間の射たちからなる指数対象であるのかは、「その対象と \(B\) との積対象が評価射を持つかどうか」によって定義付けることができる。つまり、以下のようにして定義される \({\rm isExpObj}(X,B,C)\) を満たす任意の射 \(X\) として理解する。
\[
{\rm isExpObj}(X,B,C) :\Leftrightarrow \exists e[{\rm isEvalArr}(e,X,B,C)]
\]
但し、繰り返しになるが
\[
\begin{align}
f:X\rightarrow Y :\Leftrightarrow & ({\rm \_dom}(f,X) \wedge {\rm \_cod}(f,Y)) \\
\exists ! x[P(x)] :\Leftrightarrow & \exists x[P(x) \wedge (\forall y[P(y) \Rightarrow x=y])] \\
\end{align}
\]
(..)
Exponential に関する重要な射の構成
次のページで触れるが、任意の2つの対象がその指数対象を必ず持つような圏である「カルテシアン閉圏」と呼ばれる種類の圏は関数型プログラミング言語で行われる記号操作への意味付けとして用いられる。そのため以下で紹介する重要な射の中にはプログラミング (特に Haskell) をやっている人にとってなじみ深いものが多いと思われる。
カリー化 (currying)
\({\rm curry}:C^{A\times B} \rightarrow (C^B)^A\)
\[
{\rm curry} := \lambda[\lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2 , {\rm prj}_2 \rangle \rangle {\sf \, ⨟ \,} {\rm ev}]]
\]
un-カリー化 (uncurrying)
\({\rm uncurry}:(C^B)^A \rightarrow C^{A\times B}\)
\[
{\rm uncurry} := \lambda[\langle \langle {\rm prj}_1 , {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_1 \rangle, {\rm prj}_2 {\sf \, ⨟ \,} {\rm prj}_2 \rangle {\sf \, ⨟ \,} ({\rm ev} \times B) {\sf \, ⨟ \,} {\rm ev}]
\]
内部合成 (internal composition)
\(f:A\rightarrow B\), \(g:B\rightarrow C\) を任意の射としたとき、次で定義される射 \({\rm iComp}:(B^A \times C^B) \rightarrow C^A\) は \({\rm arrToEl}(f):1\rightarrow B^A\) と \({\rm arrToEl}(g):1\rightarrow C^B\) の内部合成 \(({\rm arrToEl}(f) {\rm \: `iComp` \:} {\rm arrToEl}(g)):1\rightarrow C^A\) を提供する。
\[
{\rm iComp} := \lambda[\langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle \rangle {\sf \, ⨟ \,} (C^B \times {\rm ev}) {\sf \, ⨟ \,} {\rm ev}]
\]
pre-composition
\(X:X\rightarrow X\), \(f:A\rightarrow B\) を任意の射としたとき、
\[
X^f := \lambda[(X^B \times f) {\sf \, ⨟ \,} {\rm ev}]
\]
※ \(X^f:X^B\rightarrow X^A\) は \(\hom(f,X):\hom(B,X)\rightarrow \hom(A,X)\) とも書かれる
post-composition
\(X:X\rightarrow X\), \(f:A\rightarrow B\) を任意の射としたとき、
\[
f^X = \lambda[{\rm ev} {\sf \, ⨟ \,} f]
\]
※ \(f^X:A^X\rightarrow B^X\) は \(\hom(X,f):\hom(X,A)\rightarrow \hom(X,B)\) とも書かれる
入力のフリップ
\[
{\rm flip} := {\rm uncurry} {\sf \, ⨟ \,} C^{\langle {\rm prj}_2, {\rm prj}_1 \rangle} {\sf \, ⨟ \,} {\rm curry}
\]
タグ一覧:
