雑記帳
僕用勉強ノート 「位相空間論」の巻
商位相空間
商位相空間 (quotient topological space)
位相空間というのは、ある意味では「要素間の "並び" (空間構造) をフォーマルに規定する付加構造が指定された集合」と捉えられる。
加えて、その付加構造は「線形空間のようなリッチな数学的構造の対象が持つような付加構造」と比較すると壊れにくく、複雑で面白い操作が可能となっている。
そしてその典型的な一つが、まさにこの「商位相空間の構成」である。
定義
大雑把には「位相空間の圏における商対象」であるが、部分位相空間に関する記事でも述べたように「位相空間の圏」というのはあまり良い性質を持たない。
例えば、部分位相空間を「位相空間の圏における部分対象 (対象とモニック射の組)」として捉えることは、誤りと見做される可能性が高く、「位相空間の圏における正則部分対象 (対象と正則モニック射の組)」のみが部分位相空間であるとするというのが一般的な認識となっている。
同様に、商位相空間も「位相空間の圏における商対象」というよりかは、以下に示すような「空間内の点の集合を同値関係で割ってあげることで得られる商対象」のみを指すという認識の方が正しいかもしれない。
- \(U:\mathbf{Top}\rightarrow \mathbf{Set}\) を忘却関手
- \(X\) を位相空間
- \(\Omega\) を真理値集合
としたとき、射 \((\sim):U(X)\times U(X)\rightarrow \Omega\) という形で、
- 位相空間 \(X\) の持つ点の間の関係
を写像として定義することができる。
ここで、部分対象分類子のその射に沿う引き戻しを考えることで \(U(X)\times U(X)\) の部分対象 \(\langle R,(\sim)^{-1}({\rm true}) \rangle\) が得られ、そこから2つの射
\[
\begin{align}
(\sim)^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_1 \\
(\sim)^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_2 \\
\end{align}
\]
が構成される。
もし与えた関係が同値関係であれば、このまま集合の圏でコイコライザをとることで、「同値関係から商対象を構成する」の例でも触れたような「同値関係で割った商集合の構成」へとつながっていき、実際、そのようにして構成された商集合に位相を誘導することによって商位相空間を構成することができる。
とはいえ本当に必要になる情報は "普遍性" の方であり、このような見方だと「位相空間の圏での普遍性」が見えてきづらい。
ということで、ここでは「位相空間の圏は有限余完備である」ということを認めた上で、より見通しが良いであろう捉え方を紹介しておく。
まず、先ほど構成した2つの平行な写像 \(R \rightarrow U(X)\) というのは、
- 離散位相を指定した集合からの写像は、常に連続写像となる
ということを思い出すことによって、\(R\) に離散位相を指定して得られる位相空間 \(\langle R, {\rm arrToEl}({\rm const}({\rm true})) \rangle\) と \(X\) の間を結ぶ「位相空間の圏の射 \(\langle R, {\rm arrToEl}({\rm const}({\rm true})) \rangle \rightarrow X\)」を定めることがわかる。
つまり、「集合の圏」ではなく「位相空間の圏」の上で直接コイコライザを考えることができ、こうして得られる位相空間の圏における商対象のことを「商位相空間」と呼ぶことが多い。
因みにこの「コイコライザをとる2つの平行な射を位相空間の圏へとそのまま持っていくことができてしまう」というのがポイントで、
- トポスでない (部分対象分類子を持たない) はずの位相空間の圏で論理式を自在に使った商空間の構成が実現してしまうこと
を読み解くヒントにもなっている。
商位相空間の例
メビウスの帯 (Möbius strip)
まずメビウスの帯と聞くと、以下のような図形を思い浮かべることと思う。

まさにそうなのだが、気を付けなければいけない点があって、
- これから構成するメビウスの帯は、「メビウスの帯としての位相構造を持った位相空間」であり、上のような「3次元空間内に置かれた決まった形を持つ図形」ではない。
具体的にどういうことかなのは、議論を追っていく中でわかってくるはず。
では実際に構成していく。
まず
- \(\langle {\mathbb{R}}^2, \tau \rangle\): 2次元Euclid空間の持つ距離の構造が定める位相を持った位相空間
- \(\langle [-1,1], i \rangle\): 集合 \({\mathbb{R}}\) の部分集合
とすると、\(i\times i\) を使って 位相 \(\tau\) を集合 \([-1,1]\times [-1,1]\) に誘導することができて、それによって矩形 \(\langle [-1,1]\times[-1,1], (i\times i)^{*}\tau \rangle\) が得られる。
続いて、次のような位相空間 \(\langle [-1,1]\times[-1,1], (i\times i)^{*}\tau \rangle\) の持つ点の間の関係
\[
(x,y) \sim (x',y') :\Leftrightarrow ((x,y)=(x',y')) \vee (x=-1 \wedge x'=1 \wedge y+y'=0) \vee (x=1 \wedge x'=-1 \wedge y+y'=0)
\]
を考えると、この関係 \((\sim):[-1,1]\times [-1,1] \rightarrow \Omega\) は同値関係となる。
冒頭で説明した通り、この写像から
\[
\begin{align}
h &= (\sim)^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_1 \\
k &= (\sim)^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_2 \\
\end{align}
\]
が得られ、これらの写像は位相空間の圏の射 \(h',k'\) を定める。
そして、この2つの平行な射のコイコライザとして得られる商対象
\[
\langle \langle [-1,1]\times[-1,1], (i\times i)^{*}\tau \rangle/ \sim, {\rm Coeq}(h',k') \rangle
\]
がメビウスの帯に相当する。
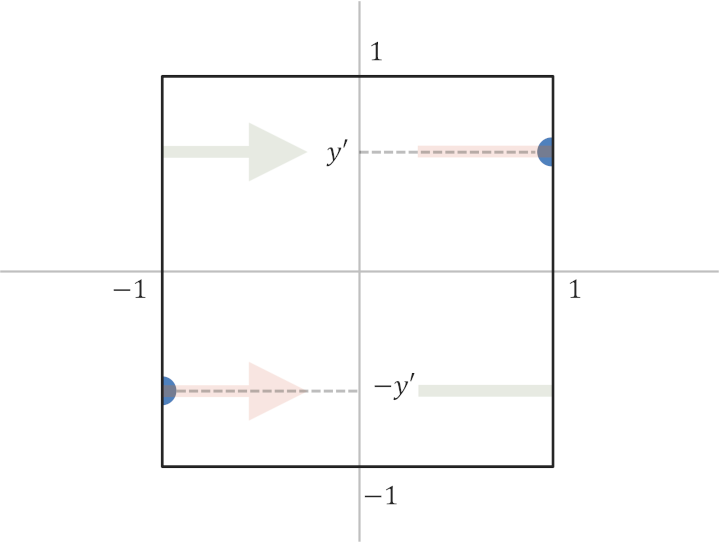
補足しておくと、同値関係を見ての通り意味としては、上の図のように
- 上下方向は行き止まりだが、左右方向は捻る形で貼り合わされたことで空間的なループができている
といったところである。
例えば
\[
(-1,-y) \sim (1,y)
\]
が成り立つので、図の中にある薄橙色の矢印方向に直進していくと、貼り合わせによって空間にループができているので、図に示したような経路をたどることになる。
余談
この例では、上下方向に空間的な行き止まりがあるが、上下方向もそのまま貼り合わせることによってクラインの壺 (Klein bottle) と呼ばれる空間を構成することができる。
興味深い話として、その空間はメビウスの帯と異なり「行き止まり」が一つもない。
ユークリッド空間では "無限遠" をとることができるため、同様に行き止まりはないが、クラインの壺の場合、空間全体が閉じている上でそうなっている。
ちなみにこの "空間に境界がない" という状況は、コンパクト性という形で厳密に説明できるようになる。
タグ一覧:
