雑記帳
トーラスの方程式
内容の修正に関して
[4/21/2024] 久しぶりに加筆をしてみたところ非常に基本的な見落としの存在に気付いたため修正。
前置き
ここで言う「トーラス (torus)」とは「2次元トーラス」のことを指している。
もう少し厳密には、位相空間として見たとき、2次元トーラスとして分類される「綺麗なドーナツ型」をした3次元ユークリッド空間の部分位相空間を意図している。
トーラスの方程式 (ベクトル方程式 ver.)
方程式
大本となる方程式

- \(r_1\): トーラスの大半径 (major radius)
- \(r_2\): トーラスの小半径 (minor radius)
- \(\boldsymbol{c}\): トーラスの中心位置
- \(\hat{\boldsymbol{n}}\): トーラスの姿勢 (トーラス上向きの単位方向ベクトル)
としたとき、トーラス上の任意の点 \(\boldsymbol{x}\) が満たすべき方程式は以下のように表される。
\[
\left\lVert \boldsymbol{x} - \left(\boldsymbol{c} + r_1 \cdot \frac{(\boldsymbol{x} - \boldsymbol{c})-(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))\hat{\boldsymbol{n}}}{\lVert (\boldsymbol{x} - \boldsymbol{c})-(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))\hat{\boldsymbol{n}} \rVert}\right) \right\rVert = r_2
\]
式の整理による簡略化を済ませた方程式
上で与えた式を整理していくと、以下の方程式が得られる。
\[
(\|\boldsymbol{x} - \boldsymbol{c}\|^2+r_1^2-r_2^2)^2-4r_1^2\cdot(\|\boldsymbol{x} - \boldsymbol{c}\|^2 - {(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))}^2) = 0
\]
中心位置と姿勢を固定して得られる方程式
先ほどの式からさらに、トーラスの上向き方向を単純な \(\boldsymbol{e}_3\) に固定したり、中心位置 \(\boldsymbol{c}\) を原点に固定したりするなりして成分に関する式に持っていくと、応用しづらくはなってしまうが
\[
(x^2 + y^2 + z^2 + r_1^2 - r_2^2)^2 - 4r_1^2\cdot(x^2 + y^2) = 0
\]
という綺麗な式が得られる。
方程式の導出
大本となる方程式
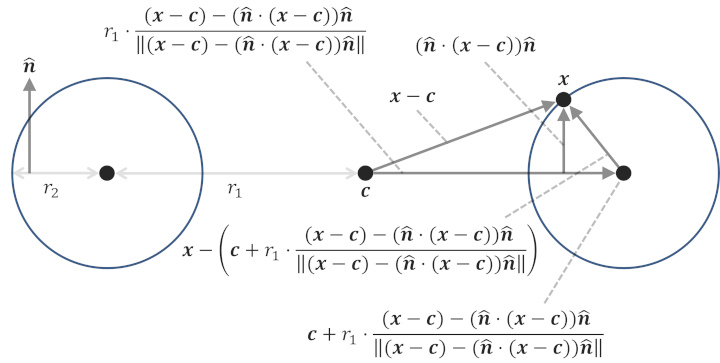
大体のことは上の図からわかると思うが、意味合いとしてはまず
- トーラス中心位置から曲面上の任意の位置までを結ぶ変位ベクトル
- その変位ベクトルの \(\hat{\boldsymbol{n}}\) 方向への射影ベクトル
の二つのベクトルの差として、トーラス中心位置からトーラス断面となる円の中心位置への方向を取得する。
続いて、その中心位置までの距離は \(r_1\) とわかっているので、先ほど求めたベクトルを規格化した上で \(r_1\) を掛ければ、その中心位置までの変位ベクトルが計算でき、さらにその変位ベクトルをトーラス中心の位置ベクトルに足してあげれば、断面部の中心位置が求まる。
最後に任意の断面部は「半径 \(r_2\) の円」でなければならないという条件を数式化すると、先ほどの方程式が得られる。
式の整理による簡略化を済ませた方程式
まず式を見やすくするために
\[
\boldsymbol{v} := \boldsymbol{x} - \boldsymbol{c}
\]
と置く。
\[
\begin{align}
\left\lVert \boldsymbol{x} - \left(\boldsymbol{c} + r_1 \cdot \frac{(\boldsymbol{x} - \boldsymbol{c})-(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))\hat{\boldsymbol{n}}}{\lVert (\boldsymbol{x} - \boldsymbol{c})-(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))\hat{\boldsymbol{n}} \rVert}\right) \right\rVert &= r_2 \\
\left\lVert \boldsymbol{v} - r_1 \cdot \frac{\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}}{\lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert} \right\rVert &= r_2 \\
{\left\lVert \boldsymbol{v} - r_1 \cdot \frac{\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}}{\lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert} \right\rVert} ^2 &= r_2^2 \\
\lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert ^2 {\left\lVert \boldsymbol{v} - r_1 \cdot \frac{\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}}{\lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert} \right\rVert} ^2 &= \lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert ^2 r_2^2 \\
\end{align}
\]
さらに
\[
\begin{align}
\mu &:= \lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert\\
\mu^2 &= \lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert ^2 \\
&= (\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}})\cdot(\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}) \\
&= (v^2 - {(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})}^2) \\
\end{align}
\]
と置いて式変形を続けると
\[
\begin{align}
\mu ^2 {\left\lVert \boldsymbol{v} - r_1 \cdot \frac{\boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}}{\mu} \right\rVert} ^2 &= \mu ^2 r_2^2 \\
{\left\lVert \mu \boldsymbol{v} - r_1 \cdot ( \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}}) \right\rVert} ^2 &= r_2^2 \mu ^2 \\
\mu^2 v^2 - 2r_1 \mu \cdot (v^2-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})(\boldsymbol{v} \cdot \hat{\boldsymbol{n}})) + r_1^2 \lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert^2 &= r_2^2 \mu ^2 \\
\mu^2 v^2 - 2r_1 \mu \cdot (v^2-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})(\boldsymbol{v} \cdot \hat{\boldsymbol{n}})) + r_1^2 \mu^2 &= r_2^2 \mu ^2 \\
\mu^2 v^2 - 2r_1 \mu \cdot (v^2-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})^2) + r_1^2 \mu^2 - r_2^2 \mu ^2 &= 0 \\
\mu^2 v^2 - 2r_1 \mu \mu^2 + r_1^2 \mu^2 - \mu ^2 r_2^2 &= 0 \\
\mu^2 v^2 - 2r_1 \mu^3 + r_1^2 \mu^2 - \mu ^2 r_2^2 &= 0 \\
\mu^2 \cdot (v^2 - 2r_1 \mu + r_1^2 - r_2^2) &= 0 \\
\mu^2 \cdot (v^2 + r_1^2 - r_2^2 - 2r_1 \mu) &= 0 \\
\end{align}
\]
上の式変形の中で暗黙的に行われている仮定に注意してほしいのだが、分母から払われる操作が行われている以上 \(\mu = \lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert\) が 0 であるケースは現時点で除外されている。
つまり
\[
\begin{align}
\mu &\ne 0 \\
\mu^2 &\ne 0 \\
\lVert \boldsymbol{v}-(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})\hat{\boldsymbol{n}} \rVert ^2 &\ne 0 \\
(v^2 - {(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})}^2) &\ne 0 \\
\end{align}
\]
ということになる。(後に同じことを話すが、実数体は零因子を持たないため、自乗を取って 0 になる要素の存在に対する心配は必要ない。)
余談
この関係式「\((v^2 - {(\hat{\boldsymbol{n}}\cdot\boldsymbol{v})}^2) \ne 0\)」を幾何学的に読み取るとするならば、「\(\boldsymbol{v}\) の方向が \(\hat{\boldsymbol{n}}\) と平行な方向を向いていない、つまりトーラス中心部から真上あるいは真下方向に進んだ先のどこかに曲面上の点が存在していない」といった感じになると思うが、仮に「ドーナツの穴がふさがっていない」ような正しいトーラスの形になるように大半径と小半径が設定されているのであれば、確かにそんな点は存在しないことがイメージできるだろう。
因みに上で「"正しい" トーラスの形」という言い回しを使っている意図は、その図形が位相空間としてみても厳密に「2次元トーラス」となるためである。
ここで繰り返しになるが実数体は零因子 (zero divisor) を持たないため、実数 \(x,y\) に対して \(xy = 0\) ならば、\(x\) か \(y\) のどちらかが 0 でなければならず、即ち
\[
\mu^2 \ne 0
\]
より
\[
v^2 + r_1^2 - r_2^2 - 2r_1 \mu = 0
\]
が満たされなければいけなくなる。
ここからさらに式変形を続けると
\[
\begin{align}
v^2 + r_1^2 - r_2^2 - 2r_1 \mu &= 0 \\
v^2 + r_1^2 - r_2^2 &= 2r_1 \mu \\
(v^2 + r_1^2 - r_2^2)^2 &= 4r_1^2 \mu^2 \\
(v^2 + r_1^2 - r_2^2)^2 - 4r_1^2 \mu^2 &= 0 \\
\end{align}
\]
最後に \(\boldsymbol{v}\) と \(\mu\) を本来の形に戻してあげれば
\[
(\|\boldsymbol{x} - \boldsymbol{c}\|^2+r_1^2-r_2^2)^2-4r_1^2\cdot(\|\boldsymbol{x} - \boldsymbol{c}\|^2 - {(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))}^2) = 0
\]
という欲しかった方程式が得られる。
中心位置と姿勢を固定して得られる方程式
まず \(\boldsymbol{x}=(x,y,z)\) とした上で、中心位置 \(\boldsymbol{c}\) と姿勢 \(\hat{\boldsymbol{n}}\) を次の形に制限する。
\[
\begin{align}
\boldsymbol{c} &=
\left[
\begin{matrix}
0 \cr
0 \cr
0
\end{matrix}
\right] \\
\hat{\boldsymbol{n}} &=
\left[
\begin{matrix}
0 \cr
0 \cr
1
\end{matrix}
\right]
\end{align}
\]
以上を踏まえてトーラスの方程式を展開していくと、
\[
\begin{align}
(\|\boldsymbol{x} - \boldsymbol{c}\|^2+r_1^2-r_2^2)^2-4r_1^2\cdot(\|\boldsymbol{x} - \boldsymbol{c}\|^2 - {(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))}^2) &= 0 \\
(\|(x,y,z) - (0,0,0)\|^2+r_1^2-r_2^2)^2-4r_1^2\cdot(\|(x,y,z) - (0,0,0)\|^2 - {((0,0,1)\cdot((x,y,z) - (0,0,0)))}^2) &= 0 \\
(\|(x,y,z)\|^2+r_1^2-r_2^2)^2-4r_1^2\cdot(\|(x,y,z)\|^2 - {((0,0,1)\cdot((x,y,z)))}^2) &= 0 \\
((x^2+y^2+z^2)+r_1^2-r_2^2)^2-4r_1^2\cdot((x^2+y^2+z^2) - z^2) &= 0 \\
(x^2+y^2+z^2+r_1^2-r_2^2)^2-4r_1^2\cdot(x^2+y^2) &= 0 \\
\end{align}
\]
つまり
\[
(x^2+y^2+z^2+r_1^2-r_2^2)^2-4r_1^2\cdot(x^2+y^2) = 0
\]
が得られた。
応用
直線との交点を求める (レイトレーシング用)
このベクトル方程式として書かれたタイプのトーラスの方程式は、「球面と直線との交点を求める」のと同じ要領で、直線との交点を求める方程式へと簡単に繋げていくことができる。
具体的には、点 \(\boldsymbol{x}_0\) を通る \(\boldsymbol{a}\) 方向に伸びる直線
\[
\boldsymbol{l}(t) = \boldsymbol{x}_0+\boldsymbol{a}t
\]
を方程式内の \(\boldsymbol{x}\) に代入するだけである。
これによって直線の媒介変数 \(t\) に関する方程式が得られ、その実数解 \(t_i\) を元々の直線の方程式に入れて得られる位置ベクトルが「直線とトーラスとの交点」ということになる。
具体的に行ってみると
\[
\begin{align}
(({\lVert \boldsymbol{x} - \boldsymbol{c} \rVert}^2+r_1^2-r_2^2)^2-4r_1^2\cdot({\lVert \boldsymbol{x} - \boldsymbol{c} \rVert}^2 - {(\hat{\boldsymbol{n}}\cdot(\boldsymbol{x} - \boldsymbol{c}))}^2)) &= 0 \\
(({\lVert (\boldsymbol{x}_0+\boldsymbol{a}t) - \boldsymbol{c} \rVert}^2+r_1^2-r_2^2)^2-4r_1^2\cdot({\lVert (\boldsymbol{x}_0+\boldsymbol{a}t) - \boldsymbol{c} \rVert}^2 - {(\hat{\boldsymbol{n}}\cdot((\boldsymbol{x}_0+\boldsymbol{a}t) - \boldsymbol{c}))}^2)) &= 0 \\
\end{align}
\]
長くなるので省略するが、ここから更に変形していくと以下の「トーラスと直線の交点を求めるための \(t\) に関する 4次方程式」が得られる。
\[
\begin{align}
0 =& \: \|\boldsymbol{a}\|^4 t^4 \\
& + \{4((\boldsymbol{x}_0-\boldsymbol{c}) \cdot \boldsymbol{a}) \|\boldsymbol{a}\|^2\} t^3 \\
& + \{2 \|\boldsymbol{x}_0-\boldsymbol{c}\|^2 \|\boldsymbol{a}\|^2 + 4((\boldsymbol{x}_0-\boldsymbol{c}) \cdot \boldsymbol{a})^2 + 2(r_1^2-r_2^2) \|\boldsymbol{a}\|^2 - 4 r_1^2 \|\boldsymbol{a}\|^2 + 4 r_1^2 (\hat{\boldsymbol{n}} \cdot \boldsymbol{a})^2\} t^2 \\
& + \{4 \|\boldsymbol{x}_0-\boldsymbol{c}\|^2 ((\boldsymbol{x}_0-\boldsymbol{c}) \cdot \boldsymbol{a}) + 4(r_1^2-r_2^2) ((\boldsymbol{x}_0-\boldsymbol{c}) \cdot \boldsymbol{a}) - 8r_1^2((\boldsymbol{x}_0-\boldsymbol{c}) \cdot \boldsymbol{a}) + 8r_1^2(\hat{\boldsymbol{n}} \cdot (\boldsymbol{x}_0-\boldsymbol{c}))(\hat{\boldsymbol{n}} \cdot \boldsymbol{a})\} t \\
& + \|\boldsymbol{x}_0-\boldsymbol{c}\|^4 + 2(r_1^2-r_2^2) \|\boldsymbol{x}_0-\boldsymbol{c}\|^2 + (r_1^2-r_2^2)^2 - 4r_1^2 \|\boldsymbol{x}_0-\boldsymbol{c}\|^2 + 4r_1^2 (\hat{\boldsymbol{n}} \cdot (\boldsymbol{x}_0-\boldsymbol{c}))^2 \\
\end{align}
\]
「図形と直線との交点を求める式」ということで、この式はレイトレーシングによる図形の描画にそのまま応用することができる。(ドーナツ型の図形をポリゴンによって作りたいという用途となると、この方程式ではなく後述する媒介変数表示の方が必要になる。)
実際に、このサイトでもトーラスと直線の交点を求める上の方程式を実践的に用いたレイトレーシングによるトーラスの画像生成も試みているので、興味があれば以下の記事も参考までに。
おまけ
xz-平面での断面の様子を z=f(x) の形で表す
中心位置と姿勢を固定して得られる方程式
\[
(x^2+y^2+z^2+r_1^2-r_2^2)^2-4r_1^2\cdot(x^2+y^2) = 0
\]
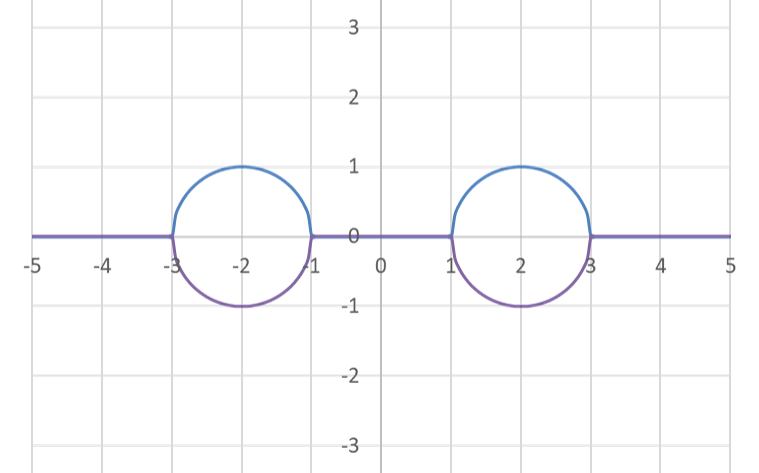
について、\(y=0\) つまり xz-平面上でのトーラスの断面の様子を特徴付ける式を求めてみる。
\[
\begin{align}
(x^2+0^2+z^2+r_1^2-r_2^2)^2-4r_1^2\cdot(x^2+0^2) &= 0 \\
(x^2+z^2+r_1^2-r_2^2)^2-4r_1^2 x^2 &= 0 \\
(x^2+z^2+r_1^2-r_2^2)^2 &= 4r_1^2 x^2 \\
x^2+z^2+r_1^2-r_2^2 &= \pm \sqrt{4r_1^2 x^2} \\
\end{align}
\]
\(r_1>r_2\) より
\[
\begin{align}
x^2+z^2+r_1^2-r_2^2 &= \sqrt{4r_1^2 x^2} \\
x^2+z^2+r_1^2-r_2^2 &= 2 r_1 |x| \\
z^2 &= 2 r_1 |x| - (x^2+r_1^2-r_2^2) \\
z &= \pm \sqrt{2 r_1 |x| - (x^2+r_1^2-r_2^2)} \\
\end{align}
\]
参考用に \(r_1=2\), \(r_2=1\) として描画した上の関数の実部のグラフを以下に載せておく。
トーラスの方程式 (媒介変数表示 ver.)
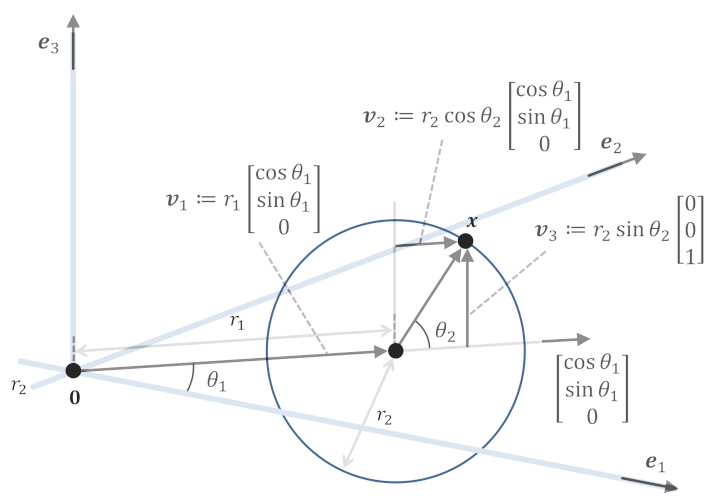
上の図を見てもらえれば \(\boldsymbol{e}_3\) を上向き方向とする大半径 \(r_1\)、小半径 \(r_2\) のトーラス上の点 \(x\) は、3つのベクトル \(\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\) の和
\[
\begin{align}
\boldsymbol{x} &= \boldsymbol{v}_1 + \boldsymbol{v}_2 + \boldsymbol{v}_3 \\
&=
r_1 \left[
\begin{matrix}
\cos \theta_1 \cr
\sin \theta_1 \cr
0
\end{matrix}
\right]
+
r_2 \cos \theta_2 \left[
\begin{matrix}
\cos \theta_1 \cr
\sin \theta_1 \cr
0
\end{matrix}
\right]
+
r_2 \sin \theta_2
\left[
\begin{matrix}
0 \cr
0 \cr
1
\end{matrix}
\right] \\
&=
\left[
\begin{matrix}
(r_1 + r_2 \cos \theta_2) \cos \theta_1 \cr
(r_1 + r_2 \cos \theta_2) \sin \theta_1 \cr
r_2 \sin \theta_2
\end{matrix}
\right]
\end{align}
\]
即ち
\[
\boldsymbol{x}(\theta_1, \theta_2) =
\left[
\begin{matrix}
(r_1 + r_2 \cos \theta_2) \cos \theta_1 \cr
(r_1 + r_2 \cos \theta_2) \sin \theta_1 \cr
r_2 \sin \theta_2
\end{matrix}
\right]
\]
という2つの媒介変数 \(\theta_1, \theta_2\) を用いた式で表すことができる。
※ここではベクトル方程式の時のように、トーラスの姿勢 (傾き方) を自由に指定できるようにしていないが、例えば「傾いたドーナツ型のポリゴンモデル」は、上の式を使って作ったポリゴンモデルを行列を使って回転させれば簡単に得ることができるため、それによる大きな不都合は特に生じない。
タグ一覧:

