雑記帳
球面の方程式
前置き
ここで言う「球面」とは「2次元球面」のことを指している。
(..)
球面の方程式 (ベクトル方程式 ver.)
(書きかけ)
方程式
大本となる方程式
- \(r\): 球面の半径
- \(\boldsymbol{c}\): 球の中心位置
としたとき球面上の任意の点 \(\boldsymbol{x}\) が満たすべき方程式は以下のように表される。
\[
\lVert \boldsymbol{x} - \boldsymbol{c} \rVert = r
\]
中心位置を原点に固定して得られる方程式
先ほどの式について、中心位置 \(\boldsymbol{c}\) を原点に固定した上で成分に関する式に持っていくと、応用しづらくはなってしまうが
\[
x^2 + y^2 + z^2 - r^2 = 0
\]
という式が得られる。
余談
非自明な項を全て左辺に纏めているのは、トーラスの記事との統一性を持たせたかっただけで、特に深い意味はない。
方程式の導出
大本となる方程式
球面の方程式は至ってシンプルで、
- 球の中心位置 \(\boldsymbol{c}\) から球面上の点 \(\boldsymbol{x}\) を結ぶ変位ベクトル \((\boldsymbol{x} - \boldsymbol{c})\) の大きさが \(r\) である。
という条件を単に数式化しただけのものである。
中心位置を原点に固定して得られる方程式
まず \(\boldsymbol{x}=(x,y,z)\) とした上で、中心位置 \(\boldsymbol{c}\) を次の形に制限する。
\[
\begin{align}
\boldsymbol{c} &=
\left[
\begin{matrix}
0 \cr
0 \cr
0
\end{matrix}
\right]
\end{align}
\]
以上を踏まえて球面の方程式を展開していくと、
\[
\begin{align}
\lVert \boldsymbol{x} - \boldsymbol{c} \rVert &= r \\
\lVert \boldsymbol{x} - \boldsymbol{c} \rVert ^2 &= r^2 \\
\left(\sqrt{(\boldsymbol{x} - \boldsymbol{c})\cdot (\boldsymbol{x} - \boldsymbol{c})}\right)^2 &= r^2 \\
(\boldsymbol{x} - \boldsymbol{c})\cdot (\boldsymbol{x} - \boldsymbol{c}) &= r^2 \\
((x,y,z) - (0,0,0))\cdot ((x,y,z) - (0,0,0)) &= r^2 \\
(x,y,z)\cdot (x,y,z) &= r^2 \\
x^2+y^2+z^2 &= r^2 \\
x^2+y^2+z^2 - r^2 &= 0 \\
\end{align}
\]
つまり
\[
x^2+y^2+z^2 - r^2 = 0
\]
が得られた。
応用
直線との交点を求める
点 \(\boldsymbol{x}_0\) を通る \(\boldsymbol{a}\) 方向に伸びる直線
\[
\boldsymbol{l}(t) = \boldsymbol{x}_0+\boldsymbol{a}t
\]
を球面の方程式内の \(\boldsymbol{x}\) に代入することで、その直線が球面上の点と交差する時の実数 \(t\) を求める方程式を得ることができる。
具体的には
\[
\begin{align}
\lVert \boldsymbol{x} - \boldsymbol{c} \rVert &= r \\
\lVert \boldsymbol{x} - \boldsymbol{c} \rVert ^2 &= r^2 \\
\lVert (\boldsymbol{x}_0+\boldsymbol{a}t) - \boldsymbol{c} \rVert ^2 &= r^2 \\
\lVert (\boldsymbol{x}_0 - \boldsymbol{c}) + \boldsymbol{a}t \rVert ^2 &= r^2 \\
((\boldsymbol{x}_0 - \boldsymbol{c}) + \boldsymbol{a}t)\cdot ((\boldsymbol{x}_0 - \boldsymbol{c}) + \boldsymbol{a}t) &= r^2 \\
\| \boldsymbol{x}_0 - \boldsymbol{c} \|^2 + 2t (\boldsymbol{x}_0 - \boldsymbol{c}) \cdot \boldsymbol{a} + \| \boldsymbol{a} \|^2 t^2 &= r^2 \\
\| \boldsymbol{a} \|^2 t^2 + \{ 2 (\boldsymbol{x}_0 - \boldsymbol{c}) \cdot \boldsymbol{a} \} t + \{ \| \boldsymbol{x}_0 - \boldsymbol{c} \|^2 - r^2 \} &= 0 \\
\end{align}
\]
つまり「球面と直線の交点」は、以下の「\(t\) に関する2次方程式」を解くことによって間接的に求めることができる。
\[
\begin{align}
0 =& \: \| \boldsymbol{a} \|^2 t^2 \\
& + \{ 2 (\boldsymbol{x}_0 - \boldsymbol{c}) \cdot \boldsymbol{a} \} t \\
& + \| \boldsymbol{x}_0 - \boldsymbol{c} \|^2 - r^2 \\
\end{align}
\]
球面の方程式 (媒介変数表示 ver.)
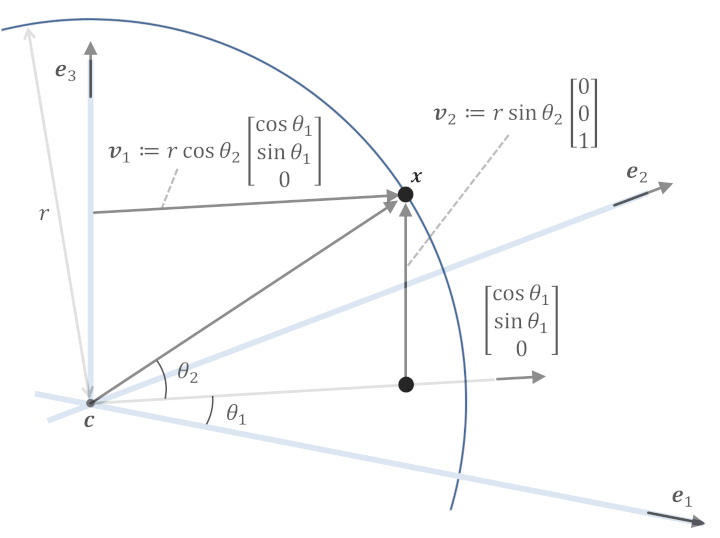
上の図を見てもらえれば半径 \(r\) の球面上の点 \(x\) は、2つのベクトル \(\boldsymbol{v}_1,\boldsymbol{v}_2\) の和
\[
\begin{align}
\boldsymbol{x} &= \boldsymbol{v}_1 + \boldsymbol{v}_2 \\
&=
r \cos \theta_2 \left[
\begin{matrix}
\cos \theta_1 \cr
\sin \theta_1 \cr
0
\end{matrix}
\right]
+
r \sin \theta_2
\left[
\begin{matrix}
0 \cr
0 \cr
1
\end{matrix}
\right] \\
&=
\left[
\begin{matrix}
r \cos \theta_2 \cos \theta_1 \cr
r \cos \theta_2 \sin \theta_1 \cr
r \sin \theta_2
\end{matrix}
\right]
\end{align}
\]
即ち
\[
\boldsymbol{x}(\theta) =
\left[
\begin{matrix}
r \cos \theta_2 \cos \theta_1 \cr
r \cos \theta_2 \sin \theta_1 \cr
r \sin \theta_2
\end{matrix}
\right]
\]
という媒介変数 \(\theta\) を用いた式で表すことができる。
(..)
タグ一覧: