雑記帳
素数計数関数 (Prime-counting function) を圏論的に構成してみる

素数計数関数を構成する
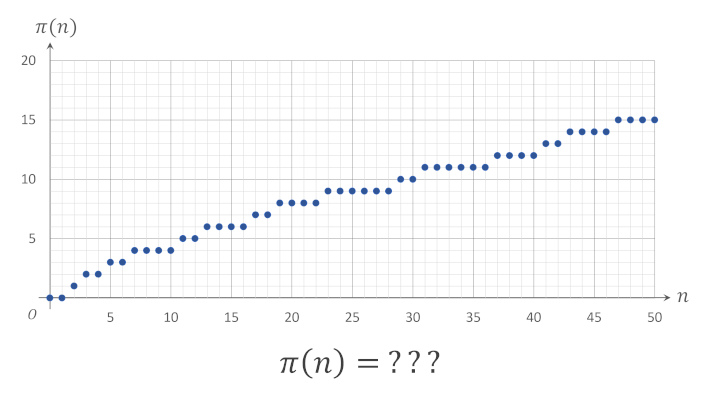
友人とかくかくしかじかあり、「素数計数関数 \(\pi:{\mathbb{N}}\rightarrow{\mathbb{N}}\)」を改めて考え直す機会があったのだけど、その際に
- あれ? この関数の構成は、圏論的な数学基礎論へのアプローチの素晴らしさ・魅力を伝えるのに最適なモノの1つではないか?
と気付いたので、記事にしてみることにした。
(..)
予備知識がない方向けの雑談
そもそも「素数計数関数」は関数と捉えて良いものなのか?
まず高等教育の文脈で「関数 (function)」という単語を聞いた場合、通常は以下のようなものたちをイメージするだろう。
- 一次関数 \(ax+b\)
- 平方関数 \(x^2\)
- 平方根 \(\sqrt{x}\)
- 三角関数 \(\cos(x)\)
- 指数関数 \(e^x\)
- 対数関数 \(\log(x)\)
さらにその通常の意味での "関数" の枠から少し外れるようなものとして
- デルタ超関数 \(\delta(x)\)
といった特殊なものが存在しているといった感じの認識になるのではないだろうか。
こういった、そのデルタ超関数ですら「似非関数」扱いされてしまう認識の中では、指定の数までの間に存在する素数の個数を与える「素数計数関数 \(\pi(n)\)」なんてものは、尚更「関数と呼べないもの」としての部類に入るようにみえてしまう。
実際、関数の厳密な定義を知らなかった当時の僕も「上に挙げた "初等的" な関数たち、加減乗除、総和記号、積分記号などの "数学チックな記号" の組み合わせとして得られるような一本の数式で書き表されたもの (+ それらの逆関数)」を漠然と "関数" と思う傾向があって、例えば階乗の
\[
n! :=
\begin{cases}
n \times (n-1)! & n > 0 \\
1 & \text{ otherwise }
\end{cases}
\]
という定義はなんちゃって定義で、ガンマ関数を使った
\[
n! := \Gamma(n+1)
\]
こそが正規の定義とすら思っていた。
ということで、
- \(\pi(n)\) = [変数 \(n\) を含む通常の数学記号の組み合わせとして書かれた一本の式]
の形で記述できるのかをイメージしづらい素数計数関数に対して、"関数" と捉えることにかなり抵抗のある人がいたとしても個人的には全く不思議ではない。
とはいえ、だからといってこの時点で「素数計数関数も似非関数である」と単に結論付けてしまうと、新たなステージに進む機会を放棄してしまうことになる。
結局関数とは何?
ではここで話を圏論に移そう。
先ほどの話では、漠然と「"数学チックな記号" の組み合わせとして得られる一本の式」を関数と捉えていたわけだが、関数をもっとプリミティブでフォーマルなパーツに細分化して考えることができたら嬉しいと思わないだろうか。
現段階における問題は、そもそも関数が何であるのかをフォーマルに説明するための数学的語彙を持ち合わせていないという点にある。
考えてみてほしいのは、第一に「数学チックな記号」はあくまで表記上の「記号」でしかなく、「その記号がどういった意味を持っているのか」という共通認識が無ければ、ただの図形に過ぎない。
そして、残念ながらその「図形に対する意味付け」が、高等教育の文脈では「数学的な式」ではなく「自然言語」によってインフォーマルに行われてしまっていることが多いのである。
つまり、本来「その図形が持っている意味の説明」の部分も数学的な問題であるはずなのだが、「自然言語」を使って "定義" したていを装ってしまうことで、そのまだ地に足ついてない未消化の問題自体の認識をしづらくしてしまっている図式になっている。
例えば「\(+\)」を例に挙げて考えてみよう。
僕たちは、「\(+\)」という記号に対して、「足し算」を想起するように教育されてきているが、「足し算であること」を数学的な語彙を使ってどのように具体的かつ厳密に噛み砕いて説明すればよいのかを改めて考えてみると難しいと感じるはずである。
これは足し算を学ぶ小学生の時点で「足し算という操作に対する数学的に厳密な定義」を教わらないので致し方ないのだが、そのままでは「足し算が結合則や交換則を満たすことの説明」がどうしてもフワッとしたバイブス頼りのものになってしまうし、結局心の底から納得できるような厳密な証明を提供することが技術的にできないのである。
ではこういった不満を解消する術はないのかというと、実はちゃんとあり、その1つに圏論というものがある。
ざっくりと説明すると、圏論ではまず「(合成の定義された) 矢印」を具体的な理論の構成要素として与え、各矢印がその合成に対して具体的にどのように振舞うのかを数学的に考えることによって、その矢印に対する自然言語に頼らない明確な意味付けを行うのである。
そして、その意味付けを行った矢印を「関数」と見做すことになる。
先の足し算を例に挙げれば、「足し算よりも根源的かつ、圏論的に直接的な意味の規定が容易な (後者関数に相当する役割を果たす) 矢印 \({\rm succ}\) の存在」を仮定することが認められる「自然数対象を持ったカルテシアン閉圏」の設定の中で、足し算それ自体を「関数」として厳密に組み立てることができる。
このように圏論は、関数とすら見做してこなかった「足し算」自体が「関数」として扱われてしまうような世界なわけだから、「素数計数関数」が先ほどの論調で「似非関数である」なんて言えなくなるのはわかってくれるだろう。
厳密にいえば、「どういった性質を課した圏」を基礎に設定するかによって、結論はもちろん変わってくるのだが、このページでは少なくともその「自然数対象を持ったカルテシアン閉圏」の設定のなかで、「素数計数関数」が「関数」つまり「圏の持つ1つの具体的な矢印」として一般的に構成できる点を示していく。
構成手順
前置き
この点だけは、通常の関数の定義方法とかなり乖離のある部分なので最初に断っておくと、その「自然数対象を持ったカルテシアン閉圏」という設定の中で行う「純粋圏論的な関数の構成」は極めて奇妙なものになる。
というのも、
- \(f(x)\) = [変数 \(x\) 含む式]
という形で、新たな関数 \(f\) を次々と定義すること自体が標準的に認められていないためである。
さらに厳密なことをいうと 関数は \(f\) だけのことを指し、\(f(x)\) はその関数 \(f\) がとる1つの「値」を指しているに過ぎない。
先ほどの (実関数としての) 三角関数を例を挙げると、\(\cos(x):1\rightarrow {\mathbb{R}}\) は値で、\(\cos:{\mathbb{R}}\rightarrow{\mathbb{R}}\) が関数として扱われるということである。
実感が持ちやすいように、もっと簡単な例である「自然数に対する平方関数 \(f\)」を用いて考えてみよう。
普通に考えれば、その関数の定義は
\[
f(n) = n^2
\]
だけで済むと思いたくなる。
しかし、そもそもまず第一に「\(n^2\)」という「絵」はなんなのか?
ここで話は少し逸れるが、わかりやすいように「集合 \(A,B\) の積集合」が「\(A\) の元 \(a\), \(B\) の元 \(b\) に対して、 \(\langle a,b\rangle\) という "記号" 全体として与えられる集合」として導入されるケースを思い浮かべてみてほしい。
まずそれの明らかな問題として、「未定義の記号(純粋数学的に意味がしっかり規定されていない記号)」からなる集合とは、果たしてなんなのかということに気付くだろう。
「記号の集合を構成する」ということ自体、割と当たり前に行われがちではあるのだが、よくよく落ち着いて考えてみるとそこには落とし穴がある。
それは、「その記号が参照するモノが純粋数学的に定義されているモノ」であるのかどうかということだ。
具体例として以下の2つを考えてみて欲しい。
- A をそのケースに収納されているポケモンカード全体の集合とする
- B を自然数全体の集合とする (但し自然数の厳密な定義は与えていない)
これらに対して違和感を覚えない人もいるかもしれないが、厳密にいうと集合という概念はそういった「記号が実世界に存在する実体を参照しているケース」とか「記号がその人の認識の中に漠然と存在する概念を参照しているケース 」とかにも対応可能な魔法の道具などでは決してなく、本来はかなりガチガチのルールに縛られた扱いにくいものなのである。(記号が直接参照できるのは、基本的に純粋数学の世界の住人に限られる。)
ちなみに「記号のカタチを見ればそんなの一目瞭然でしょ?」と言いたい人もいるかもしれないが、そうやって記号を “絵” として捉えることも実はマズい。
なぜなら、その “絵” \(\langle a,b\rangle\) からその絵の中に部分的に含まれるアルファベットの絵「\(a\)」をラベル付けしている「対象 \(A\) の要素」を取り出す “手続き” が具体的にどのような数学的実体として実現するのかという問題がうやむやにされているためである。
仮に人やコンピュータがその絵から意味を類推できたとしても、その手続きは人やコンピュータによって処理される、つまり「記号から意味を汲み取る教育の施された人間の存在」あるいは「記号から意味を汲み取るソフトウェアの存在」を想定しなければならず、それでは純粋数学の世界だけで話をしっかり完結させることができず曖昧さも取り除ききれない。
概念的な話ばかりしていてもちょっと実感を持ちづらいかもなので、実際の現場ではどのようになっているのかを例としてあげておこう。
例えば ZFC と呼ばれる集合論は \(\langle a,b\rangle\) を具体的な数学的実体への識別子としての記号 \(\{\{a\},\{a,b\}\}\) の別表記として通常与えることになるし、 ETCS と呼ばれる集合論では \(\langle a,b\rangle\) を積対象の普遍性により意味付けられた具体的な数学的実体である矢印への識別子として与えている。
さて話が散らかってしまったが、同様の問題が「\(n^2\)」という表記にも付きまとう。
「\(n\)」という絵の右上にちょこっと小さい 2 が書かれていたところで、その絵はみた通りのなんでもない絵 / 記号に過ぎない。
わかりやすく言い換えるならば、その記号が絶対的に持つ「全宇宙で普遍の意味」とやらは存在しないということである。
重要なのは、「\(n^2\)」という記号の "形状" ではなく、僕たち地球人がその記号に対して共通認識として持っている「ある自然数の2乗」という “意味” の方であり、これから圏論的基礎に基づきながら、その「意味」を純粋数学的実体として直接具現化していくのである。
何か大層な話に聞こえるかもしれないが、そんなに難しく考える必要もなくて、この場合は大まかに、「与えられた自然数の2乗を取る」という手続きを
- 与えられた自然数を2つに複製する関数
- 自然数の対からそれら自然数の積を取る関数
といった感じに細分化して捉えると、「ある自然数の2乗」を上手く純粋数学的に地に足ついたカタチにすることができる。
それら関数が具体的にどういった純粋数学的実体であるのかについては自然数対象の記事等を確認してほしいのだが、結果だけ示すとこの設定において自然数に対する平方関数 \(f\) は
\[
f = \langle {\mathbb{N}},{\mathbb{N}} \rangle {\sf \, ⨟ \,} (({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\rm const}({\rm zero})),\lambda[\langle {\rm ev}, {\rm prj}_2 \rangle {\sf \, ⨟ \,} (({\rm rec}_{{\mathbb{N}}}({\rm arrToEl}({\mathbb{N}}),\lambda[{\rm ev} {\sf \, ⨟ \,} {\rm succ}])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev}) ])\times {\mathbb{N}}){\sf \, ⨟ \,} {\rm ev})
\]
という形で構成できる。
よく考えてみれば、そもそも
\[
f(n) = n^2
\]
で \(f\) を定義しようとすること自体、はなからおかしいのである。
確かに正統派な数学を学んできている場合、今まで、
\[
f = f_2 \circ f_1
\]
のような合成関数以外に
\[
f = \text{\(...\)}
\]
の形式で関数 \(f\) が "具体的" に定義されてきた前例を殆ど見てこなかったと思うので、関数は「f(x)=...」の式を介して定義されるものみたいな認識があるかもしれない。
しかし圏論レベルで見れば、それは単なる「1つの関係式」に過ぎず、その関係式を満たすような数学的実体 \(f\) が実際に存在するのかという点は、もちろん自明ではない。(基礎にトポスを設定すればそういった構成も不可能ではないが、少なくとも現在の「自然数対象を持つカルテシアン閉圏」の設定の中では基本的に無理である。)
以上の「自然数の平方関数」の構成を見てもわかると思うが、圏論ベースに考える場合、関数は「自明ともいえるかなり基本的な部品をゴリゴリと組み合わせて欲しいカタチにしていく」といったアプローチで構成することになる。
当然、物事は非常に煩雑にはなるが、「低レベルな操作」を使える強みもあり、なんとこれから考えていきたい「素数計数関数」も、この平方関数の構成の延長としてそのまま考えることができるのである。
(..)
Haskell での動作確認
いつも通り Haskell プログラムで動作検証をしておく。
ページ最後に載せたコードを確認すればわかるように、 main
main というラベルが付けられる値には
というラベルが付けられる値には
 main
main というラベルが付けられる値には
というラベルが付けられる値には- 圏論的に構成された素数計数関数に 0 から 50 までの値を入力して得られる値を全て出力する IO アクション
を割り当てているが、それを実行すると以下が得られる。
ghci> main
pi(0) = 0
pi(1) = 0
pi(2) = 1
pi(3) = 2
pi(4) = 2
pi(5) = 3
pi(6) = 3
pi(7) = 4
pi(8) = 4
pi(9) = 4
pi(10) = 4
pi(11) = 5
pi(12) = 5
pi(13) = 6
pi(14) = 6
pi(15) = 6
pi(16) = 6
pi(17) = 7
pi(18) = 7
pi(19) = 8
pi(20) = 8
pi(21) = 8
pi(22) = 8
pi(23) = 9
pi(24) = 9
pi(25) = 9
pi(26) = 9
pi(27) = 9
pi(28) = 9
pi(29) = 10
pi(30) = 10
pi(31) = 11
pi(32) = 11
pi(33) = 11
pi(34) = 11
pi(35) = 11
pi(36) = 11
pi(37) = 12
pi(38) = 12
pi(39) = 12
pi(40) = 12
pi(41) = 13
pi(42) = 13
pi(43) = 14
pi(44) = 14
pi(45) = 14
pi(46) = 14
pi(47) = 15
pi(48) = 15
pi(49) = 15
pi(50) = 15以上の結果を見れば、構成に誤りがないことを信じてもらえるのではないだろうか?
因みに、「その関数が自然数対象を持つカルテシアン閉圏という弱い設定の中でも数学的に構成できる事実 (構成に部分対象分類子の存在のような強い公理が必要とならない等)」の部分を手っ取り早く示すことにウェイトを置いているため、実行パフォーマンスは非常に悪い。
実際に、自身でもこの Haskell プログラムを動かしてみれば体感できると思うが、 \(\pi(50)\) の計算でさえも手間取る有様となっている。
ソースコード
{-# LANGUAGE TypeOperators #-}
import Data.Void
main :: IO ()
main = do
foldr (>>) (return ()) $ do
n <- [0..50]
return $ do
putStrLn $ "pi(" ++ (show n) ++ ")\t= " ++ (showEl $ nat(n) -: primeCountingFnc)
class (MyShow a) where
myShow :: a -> String
instance MyShow () where
myShow = const "*"
instance (MyShow a, MyShow b) => MyShow (Either a b) where
myShow = either
(\z -> if (myShow z == "*") then "inj1" else (myShow z) ++ ";inj1")
(\z -> if (myShow z == "*") then "inj2" else (myShow z) ++ ";inj2")
instance (MyShow a, MyShow b) => MyShow (a,b) where
myShow (x,y) = "(" ++ myShow x ++ "," ++ myShow y ++ ")"
instance MyShow Int where
myShow = show
instance MyShow Nat where
myShow (Nat i) = myShow (length i)
--myShow (Nat i) = "zero" ++ (foldr ((++).(const ";succ")) [] i)
instance MyShow (a -> b) where
myShow = const "(AN ARROW)"
-- X の要素を圏論に倣って終対象から X への射(Global element)として扱うための関数
el :: a -> (Pt -> a)
el = (const::a -> (Pt -> a))
-- Global elements 用 ユーティリティ
(===) :: Eq a => (Pt -> a) -> (Pt -> a) -> Bool
(===) x y = (x() == y())
showEl :: MyShow a => (Pt -> a) -> String
showEl x = (myShow $ x())
printEl :: MyShow a => (Pt -> a) -> IO ()
printEl = putStrLn . showEl
-- Diagrammatic-order な射の合成演算
(-:) = flip (.)
-- # 始対象と終対象
type Empty = Void
type Pt = ()
initArr :: Empty -> a
initArr = absurd
termArr :: a -> Pt
termArr = const ()
point :: Pt -> Pt
point = id
const' x = termArr -: x
-- # 余積対象と積対象
type (+++) a b = Either a b
type (***) a b = (a,b)
-- 入射
inj1 :: a -> a +++ b
inj1 = Left
inj2 :: b -> a +++ b
inj2 = Right
-- 射影
prj1 :: a *** b -> a
prj1 = fst
prj2 :: a *** b -> b
prj2 = snd
-- 余積対象の仲介射
coPair :: (a -> c, b -> c) -> (a +++ b -> c)
coPair = uncurry either
-- 積対象の仲介射
pair :: (c -> a, c -> b) -> (c -> a *** b)
pair = uncurry $ (<*>) . fmap (,)
-- 畳み込み
fol = coPair(id, id)
-- 対角射
dup = pair(id, id)
-- 射同士の余積
(+++) :: (a1 -> b1) -> (a2 -> b2) -> (a1 +++ a2 -> b1 +++ b2)
(+++) f g = coPair(f -: inj1 , g -: inj2)
-- 射同士の積
(***) :: (a1 -> b1) -> (a2 -> b2) -> (a1 *** a2 -> b1 *** b2)
(***) f g = pair(prj1 -: f, prj2 -: g)
-- Twist の形式的双対
coTw :: a +++ b -> b +++ a
coTw = coPair(inj2, inj1)
-- Twist
tw :: a *** b -> b *** a
tw = pair(prj2, prj1)
-- # Exponential 対象
type (^) b a = a -> b
-- 評価射
ev :: (b ^ a) *** a -> b
ev = uncurry id
-- 射の転置 (transpose) の構成
trans :: (c *** a -> b) -> (c -> b ^ a)
trans = curry
-- 射 h:a->b の Exponential 対象 (Exp b a) の要素への変換
arrToEl :: (a -> b) -> (Pt -> b ^ a)
arrToEl h = trans(prj2-:h)
elToArr x = pair(termArr, id) -: (x *** id) -: ev
curry' :: (c ^ (a *** b)) -> (c ^ b) ^ a
curry' = trans(trans(pair(prj1 -: prj1, pair(prj1 -: prj2, prj2)) -: ev))
uncurry' :: (c ^ b) ^ a -> (c ^ (a *** b))
uncurry' = trans(pair(pair(prj1,prj2 -: prj1), prj2 -: prj2) -: (ev *** id) -: ev)
iComp :: ((b^a) *** (c^b)) -> c^a
iComp = trans(pair(prj1 -: prj2, pair(prj1 -: prj1, prj2)) -: (id *** ev) -: ev)
flip' :: ((c^b)^a) -> ((c^a)^b)
flip' = uncurry' -: trans((id *** tw) -: ev) -: curry'
-- # 自然数対象 (NNO)
data Nat = Nat{imp::[()]} deriving Eq
_Nat :: Nat -> Nat
_Nat = id
zero :: Pt -> Nat
zero = el (Nat [])
succ' :: Nat -> Nat
succ' (Nat i) = Nat (():i)
-- 整数リテラルを使って NNO の Global elements としての自然数を得るための小細工
nat :: Int -> (Pt -> Nat)
-- nat i = zero -: (foldr (.) id (replicate i succ'))
nat i = el (Nat (replicate i ()))
-- recursion data x_0:1->X と f:X->X から rec_N(x_0, f):Nat->X を構成する関数
rec_N :: (Pt -> a, a -> a) -> (Nat -> a)
rec_N = ((flip ($) ())***id)-:((curry((id***(length.imp))-:uncurry(!!))).(uncurry.flip $ iterate))
iterate' :: x *** (x ^ x) -> (x ^ Nat)
iterate' =
trans(pair(pair(prj2, prj1 -: prj2), prj1 -: prj1) -:
pair(const'(arrToEl(rec_N(arrToEl(const'(arrToEl(id))),trans(pair(prj2,ev) -: iComp))) -:
uncurry' -: uncurry'), id) -: ev)
add_N = (rec_N(arrToEl(_Nat), trans(ev-:succ'))***_Nat)-:ev
mul_N = (rec_N(arrToEl(termArr-:nat(0)), trans(pair(ev,prj2)-:add_N))***_Nat)-:ev
mul_N_fast (Nat x, Nat y) = Nat (replicate (length x * length y) ()) -- デバッグ用
sq_N = dup-:mul_N
pred' = rec_N(pair(nat(0),nat(0)), pair(prj2, prj2 -:succ')) -: prj1
sub_N = tw-:(rec_N(arrToEl(_Nat), trans(ev-:pred'))***_Nat)-:ev
true :: Pt -> Nat
true = nat(1)
false :: Pt -> Nat
false = nat(0)
if' :: Nat *** (Nat *** Nat) -> Nat
if' =
pair(pair(prj1,prj2-:prj1),prj2-:prj2) -: pair(pair(prj1-:prj1-:normalize, prj1-:prj2)-:
mul_N, pair(prj1-:prj1-:not'-:normalize,prj2)-:mul_N)-:add_N
le' :: Nat *** Nat -> Nat
le' = sub_N -: not'
eq' :: Nat *** Nat -> Nat
eq' = pair(le',tw-:le')-:and'
not' :: Nat -> Nat
not' = pair(const'(nat(1)),id) -: sub_N
and' :: Nat *** Nat -> Nat
and' = mul_N
or' :: Nat *** Nat -> Nat
or' = add_N
normalize :: Nat -> Nat
normalize = rec_N(pair(nat(0),nat(1)), pair(prj2, prj2)) -: prj1
f1 :: (Nat *** Nat) -> (Nat *** Nat)
f1 = const'(pair(nat(0),nat(0)))
f2 :: ((Nat *** Nat) *** (Nat *** Nat)) -> (Nat *** Nat)
f2 =
pair((prj2-:prj1)-:succ',pair((prj2-:prj2),pair(pair(pair((prj2-:prj1),const'(nat(1)))-:
(le'),pair((prj2-:prj1),(prj1-:prj2))-:(eq'))-:(or'),pair(const'(nat(0)),pair(pair((prj1-:
prj1),(prj2-:prj1))-:(mul_N),(prj1-:prj2))-:(eq')))-:if')-:(add_N))
-- [$3;succ',[$4,[[[$3,const'(nat(1))];(le'),[$3,$2];(eq')];(or'),[const'(nat(0)),[[$1,$3];(mul_N),$2];(eq')]];if'];(add_N)]
f3 :: ((Nat *** Nat) *** Nat) -> (Nat *** Nat)
f3 = ((pair(f1,trans(f2))-:iterate')***id)-:ev
f4 :: (Nat *** Nat) -> Nat
f4 = pair(id,prj2)-:f3-:prj2
-- [$2;succ',[$3,[[[$2,const'(nat(1))];(le'),[$2,$1];(eq')];(or'),[const'(nat(0)),[$2,$1];f4]];if'];(add_N)]
g1 :: Nat -> (Nat *** Nat)
g1 = const'(pair(nat(0),nat(0)))
g2 :: (Nat *** (Nat *** Nat)) -> (Nat *** Nat)
g2 =
pair((prj2-:prj1)-:succ',pair((prj2-:prj2),pair(pair(pair((prj2-:prj1),const'(nat(1)))-:
(le'),pair((prj2-:prj1),(prj1))-:(eq'))-:(or'),pair(const'(nat(0)),pair((prj2-:prj1),(prj1))-:
f4))-:if')-:(add_N))
g3 :: (Nat *** Nat) -> (Nat *** Nat)
g3 = ((pair(g1,trans(g2))-:iterate')***id)-:ev
isPrime :: Nat -> Nat
isPrime = dup-:g3-:prj2-:not'
primeCountingFnc :: Nat -> Nat
primeCountingFnc =
rec_N(pair(nat(1),nat(0)),pair(prj1-:succ',pair(prj2,prj1-:isPrime)-:(add_N)))-:prj2-:pred'タグ一覧:
