雑記帳
位置ベクトルと方向ベクトル
(書きかけ)
3次元ユークリッド空間内の矢印を使って捉える場合
位置ベクトル
捉え方
任意の3次元ユークリッド空間内の一点 \(A=(x,y,z)\) が与えられたときに、点 \(A\) の 位置ベクトル (position vector) とは、「原点 \(O\) と 点 \(A\) を結ぶ矢印 \(\overrightarrow{OA}=(x,y,z)\)」として描かれるものを指す場合がある。
ここで、「空間内の一点 \(A=(x,y,z)\)」と「原点とその点を結ぶ矢印 \(\overrightarrow{OA}=(x,y,z)\)」について、それぞれが同じもの \((x,y,z)\) を指し示している部分が注意するべき点の1つとしてある。
例えば、上の \(\overrightarrow{OA}\) という表記の場合は混同しづらいが、例えば物理学において位置ベクトルは \(\boldsymbol{r}\) とかかれ、さらにそれは
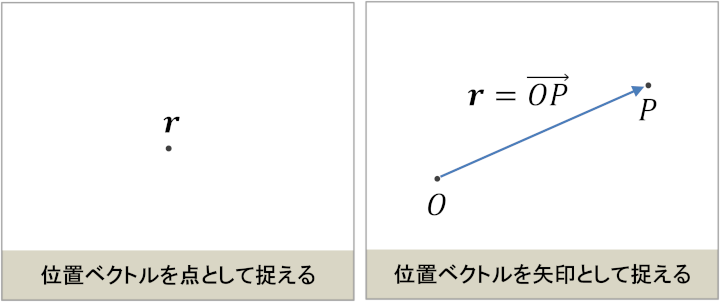
- 原点 \(O\) と空間内のある一点 \(P\) を結ぶ矢印 \(\boldsymbol{r} = \overrightarrow{OP}\) (\(\boldsymbol{r}\) を矢印 \(\overrightarrow{OP}\) として扱う)
ではなく、
- 空間内の一点 \(\boldsymbol{r}\) そのもの (\(\boldsymbol{r}\) それ自体を空間内の1つの位置として扱う)
というように、「矢印」としての姿ではなく、「点」そのものとして位置ベクトルを捉えるケースもある。
余談
このサイトでは、位置ベクトルは「原点を始点に持つ矢印」ではなく、「単なる空間の一点」の方で考えている。
では「位置ベクトルとは何か」という明確な答えはないのかということになるが、これについては「そもそもベクトルとは何か」という話に繋がり、このページの後半部分で説明している。
もし抽象的な話でもドンとこいという場合であれば、是非読んでみて欲しい。
位置ベクトルを単なる1点として扱う場合の注意点
位置ベクトルを「単なる点」として扱う場合、注意しなければならない点がいくつか存在する。
1つ目は、「位置ベクトルが持つ加法が原点の位置に依存する点」である。
例えば、理論物理学で「空間内での座標系によらない自然な現象の記述」を考えていくために、しばしばベクトルを使用するのだが、そういった状況を思い浮かべてみてほしい。
その場合、「どの位置が原点になっているユークリッド空間をモデルとして選択しているのか」というのも当然考えないため、そのユークリッド空間でモデル化した世界の中での原点の位置というのは、(どの向きが \(x\) 軸であるかと同様) 根本的に「不明 (絶対的な意味を持たないもの)」という扱いになる。
つまり「原点の明確な位置が決められていない状況下」では、位置ベクトル同士の和を (物理的に明確な意味を見出せる演算として) 定めようがないため、一般的な「位置ベクトル同士の足し算」というのは、そのような座標フリースタイルで現象を記述していく中では (式変形の過程で現れることはあっても直接的に行うことは) 物理的にナンセンスであることになる。
では、位置の足し算やスカラー倍に意味がないのに、どうしてわざわざ位置をベクトルとして取り扱うのかという話になるのだが、実は何もかもが全て無意味というわけでもなくて、物理的に意味のある便利な操作も含んでいる。
例えば「位置に変位を加える操作」や「2つの位置の変位を求める操作」などの原点の位置に依存しない操作がその典型になるのだが、詳しくは方向ベクトルの節で考えていく。
方向ベクトル
(..)
少しフォーマルに捉える場合
ベクトルは線形空間の構造が与えられて初めて決まる相対的な概念?
そもそもベクトルとは?
「ベクトル」というと「矢印」を指す言葉というイメージがあるかもしれないが、一般に「ベクトル」と呼ばれるモノは「何か決まった特定の実体あるモノ」を絶対的に指し示しているわけではない。
では具体的にベクトルとは一体なんであるのかというと
- あるモノの集まりがあって、それらの間に特定の条件を満足する演算を定義することができるとき、そのモノをベクトルと呼ぶことにしよう
といった感じに相対的に定義される概念となっている。
数学用語を用いて言い換えるのであれば、
- 線形空間の基底集合の要素
をベクトルと呼び、つまるところ何らかの先行して与えられた「線形空間」という構造から相対的に定まる概念という立ち位置にある。
ベクトルとして見做せるモノの例
ベクトルという概念は何らかの線形空間の枠組みが与えられて初めて見出すことのできる概念であることを先ほど強調した。
これが意味するのは、「(潜在的に) ベクトルと "見做せる" モノ」であったとしても、「(特定の線形空間の構造が明示的に指定されることなしに) そのモノそれ自体をベクトルと呼ぶことはできない」ということになる。
少し回りくどいかもしれないが、言いたいこととしては「あるモノをベクトルとして捉えるよりも前に、そのモノが先行して与えられる」ということである。
具体例として、「実数の3つ組 \((x,y,z)\)」を考える。
その3つ組は、ベクトル (線形空間の基底集合の要素) であることとは関係なしに与えることが可能であることは納得してもらえるだろう。
ここで、その3つ組に対する成分同士の加法とスカラー倍の構造を指定することによって、その実数の3つ組全体の集合を基底集合にとる1つの線形空間の構造を得ることができる。
そして、その線形空間の枠組みから3つ組 \((x,y,z)\) を相対的に見ることによって初めて、\((x,y,z)\) をベクトルとして見ることが可能になる。
この記事の冒頭で行った「数の組 \((x,y,z)\)」に対し、後から同じものを指して「ベクトル」と呼んでいる部分も、この見方からフォーマルに説明されることになる。
もしかすると、以上の説明について
- でも、余計なワンステップをわざわざ踏まなくても、ベクトルとして見做せることがわかっているのだから、\((x,y,z)\) を素直にベクトルと直接呼んだほうがわかりやすいよね
と考える人もいるかもしれないので少し補足しておくと、
- 3つ組 \((x,y,z)\) をベクトルと見做す方法は無限通りあり、\((x,y,z)\) を3次元ベクトルと見做す方法だけに限らず、1次元ベクトルや7次元ベクトルと見做したりすることも可能。(具体的には、実数の3つ組全体の集合と実数の7つ組全体の集合との間に同形射が存在するため、その同形射を用いて7つ組全体の集合に自然に入る加法とスカラー倍を3つ組全体の集合に持ってくることが可能であり、それによって「実数の3つ組全体の集合を基底集合にとる7次元線形空間」の構造を得ることができてしまう。)
という事実があるため、そういった見方はあまり適切とは言えない。
最後に3つ組以外にも潜在的にベクトルになるモノの例を幾つか挙げておくと、
- 矢印
- 歪みのない空間内の位置 (空間内の一点)
- 量子状態
- ある集合から体の基底集合への写像
- 斉次線形微分方程式の解
などがある。
位置ベクトル
そもそも位置とは?
そもそも数学的に「位置」とは何なのかという話だが、これについては幾つかの捉え方があり、そのどれにも共通するのは「空間内の1点」ということである。
そして「空間とは何であるのか」という新たに生まれる問い対して、異なる幾つかの回答が知られている。
空間とは何であるのかに対する幾つかの答え
良く知られている「空間とは何か」という問いに対する1つの答えは「位相空間 (topological space)」である。
(..)
他にも、圏論的な考え方が広がっていく中で、「ロケール (locale)」と呼ばれる種類の数学的構造も、その回答の1つとして考えられるようになっている。
(..)
空間の点
位相空間の場合、
- 先に点の集まりを与え、その集まりに対して特定の公理を満たす位相構造を指定することによって、その集まりを基底集合にとる位相空間を得る
という流れになる。
つまり、「位相空間の点とは何か?」と言われれば、それは言うまでもなく「位相空間の基底集合の要素」になる。
一方で、圏論が登場したことによって「図形を点の集まり」として捉えるのではなく、「先行する点の概念無しに、点が存在する場所となる空間を直接定義する」ということを考えることができるようになった。
そういった抽象的な空間の定義を考えていく中で、空間 \(X\) 内の1点 \(x\) というのは、「その空間全体の成す圏 \(\mathscr{C}\) の中の射 \(x:pt\rightarrow X\) (但し、\(pt\) は \(\mathscr{C}\) の持つ終対象)」という一貫した形で "定義" を行うことが可能であることもわかってきた。
位相空間を例に挙げれば、位相空間 \(X=\langle P_X,\tau_X \rangle\) 内の点 \(x\) は、「位相空間の圏の射 \(x:pt \rightarrow X\)」になるが、ここで \(pt\) は離散位相を持っているため、集合 \(\hom_{\mathbf{Top}}(pt,X)\) は \(\hom_{\mathbf{Set}}(1,P_X)\) つまり指数集合 \((P_X)^1\) と見做されるのだが、これは実質 \(X\) の基底集合 \(P_X\) であり、この「終対象からの射としての位相空間の点の定義」が大本の解釈と同値であることがわかる。
これだけ見れば、この「空間の点の定義」は単に物事を複雑にしているだけの蛇足にしか見えないが、もう1つの別の種類の空間である「ロケール」については、このスタイルでの空間の点の定義が先行して必要になる。
(さらに集合の点やトポス持つ対象の点などでもこの定義が一貫して通用する。)
(..)
ここまで色々と話してきたが、何が言いたいのかといえば、空間 \(X\) が与えられたとき、「位置」即ち「空間の点」全体の集合 \(\hom_{\mathscr{C}}(pt,X)\) から、その集合を基底集合にとる線形空間の構造を導く一般的な自明な手続きはないということである。
もっと簡潔にいうならば、「位置 (空間の1点) は数学的に厳密に定義できても、必ずしもそれをベクトルとして見做せるとは限らない」ということになる。
方向ベクトル
(..)
方向ベクトルは、1つの見方としては、「滑らかな多様体の各点で定義される接空間の持つベクトル」として捉えられる。
まとめ
有向線分として表される空間ベクトルとして見た場合には明確な区別がされない「位置ベクトル」と「方向ベクトル」であったが、抽象的な数学的構造レベルにまで戻って考えてみると、それらは明確に区別され
- 位置ベクトル: 「位置」はそもそも一般にはベクトルとして見ることができず、ユークリッド空間では例外的にベクトルと見做せていただけに過ぎない。
- 方向ベクトル:
といったところになるだろう。
タグ一覧:
