雑記帳
指定の2つの自然数の対の集まりに対する、それらペアとなる数の差の2乗の総和の一般式を求める問題
問題4
自然数 \(1,2,3,...,n\) から異なる2つを選ぶ全ての組み合わせについて、2数の差の2乗の和を \(S_n\) とする。例えば
\[
S_3 = (1-2)^2 + (1-3)^2 + (2-3)^2
\]
である。この時、\(S_n\) を求めよ。
解答例
この問題の終着点は「総和の一般式」を求めることであるが、そのためにはまず問題として与えられている式の中から「規則 / パターン」を見出すことが必要になる。
まず具体例として \(S_3\) の場合を考えてみる。
\[
S_3 = (1-2)^2 + (1-3)^2 + (2-3)^2
\]
いきなりここからパターンを見つけ出せと言われてもやはり難しいので、ここで一つ、パターンを見つけるのに役立つ一つの流れを紹介する。
(ちなみに、一番やってはいけないのは、「1+4+1」というように各項を先に計算してしまうこと。これをしてしまうと、パターンが見出しづらくなってしまう。)
(ちなみに、一番やってはいけないのは、「1+4+1」というように各項を先に計算してしまうこと。これをしてしまうと、パターンが見出しづらくなってしまう。)
#1. 各項がどういった変数 \(a,b,c...\) を引数に持つ関数 \(f\) の値として表現されているのか?
#2. その関数 \(f\) の引数に代入されることになる値の全容はどうなっているのか?
(#3. その関数 \(f\) がどういった良い性質を持っているのか?)
#2. その関数 \(f\) の引数に代入されることになる値の全容はどうなっているのか?
(#3. その関数 \(f\) がどういった良い性質を持っているのか?)
まず #1 から始める。
「各項がどういった変数 \(a,b,c...\) を引数に持つ関数 \(f\) の値として表現されているのか?」ということであるが、具体的には
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
という3つの項がそれぞれどういった関数の値 \(f(a,b,...)\) として表現できるのかを考えたいわけである。
「各項がどういった変数 \(a,b,c...\) を引数に持つ関数 \(f\) の値として表現されているのか?」ということであるが、具体的には
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
という3つの項がそれぞれどういった関数の値 \(f(a,b,...)\) として表現できるのかを考えたいわけである。
一見難しそうであるが、設問をしっかりと読み返せばちゃんとそこに答えは書いてある。
つまり
「自然数 \(1,2,3,...,n\) から異なる2つを選ぶ全ての組み合わせについて、2数の差の2乗」
という部分である。
「自然数 \(1,2,3,...,n\) から異なる2つを選ぶ全ての組み合わせについて、2数の差の2乗」
という部分である。
もっとわかりやすく文章を簡潔に書き換えると、
「2つの数 \(a,b\) について、それら2つの数 \(a,b\) の差 \((a-b)\) の2乗 \((a-b)^2\)」
ということである。
(「1以上n以下の自然数である」とか「異なる2つである」とかは #2 で考えるので、この #1 の段階ではスルーしてよい。)
「2つの数 \(a,b\) について、それら2つの数 \(a,b\) の差 \((a-b)\) の2乗 \((a-b)^2\)」
ということである。
(「1以上n以下の自然数である」とか「異なる2つである」とかは #2 で考えるので、この #1 の段階ではスルーしてよい。)
まとめると、各項は次で定まる関数 \(f\) の値として表現できなければならない。
\[
f(a,b) = (a-b)^2
\]
事実、最初に与えた
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
というのは次のように漏れなく全て、先ほど定めた関数 \(f\) の値として表現できる。
\[
\begin{align}
(1-2)^2 &= f(1,2) \\
(1-3)^2 &= f(1,3) \\
(2-3)^2 &= f(2,3) \\
\end{align}
\]
#1 の問題が解決したので、続いて #2 の問題について考える。
「その関数 \(f\) の変数 \(a,b\) に代入されることになる値の全容はどうなっているのか?」ということであるが、今の \(S_3\) の例でいえば関数 \(f\) を使って次の3つの項を求める際に使用している引数 \((a,b)\) の全容 \(X_3\) (ちなみに \(X_3\) は集合) を知りたいわけである。
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
1. \((1-2)^2\)
2. \((1-3)^2\)
3. \((2-3)^2\)
これについては先ほども見た通り、
\[
\begin{align}
(1-2)^2 &= f(1,2) \\
(1-3)^2 &= f(1,3) \\
(2-3)^2 &= f(2,3) \\
\end{align}
\]
であるので、明らかに
\[
X_3 = \{(1,2), (1,3), (2,3)\}
\]
となる。
(#3 については、また後で考えるので一旦先に進む。)
ここでネタバラシになるが、ここまでわかれば形としては
\[
\begin{align}
\sum_{(a,b) \in X_3} & f(a,b)\\
\sum_{x \in X_3} & f(x)\\
\end{align}
\]
というように、綺麗に総和の記号を使って書くことができる。
つまりは、見事パターン化に成功し、当初の目的は果たせたということである。
... とはいえ、今知っている便利な公式は
... とはいえ、今知っている便利な公式は
\[
\begin{align}
\sum_{a=1}^{n} a &= 1 + 2 + \cdots + n \\
&= \frac{n(n+1)}{2} \\
\end{align}
\]
であり、残念ながらこの種の「集合を使った総和」に対する一般式には有効ではなく、引き続き小細工が必要になってしまう。
何が問題であるかといえば、総和を取られるペアの全体 \(X_3\) が不規則に見える点である。
実際、表にまとめて視覚化してみよう。
実際、表にまとめて視覚化してみよう。
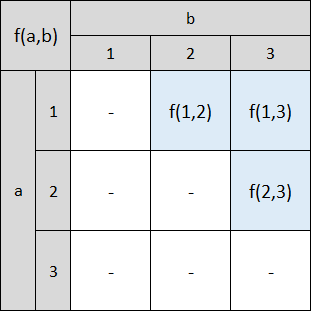
見ての通り、値がまばらに配置されていてマスが虫食い状態になっているがために、それらの総和に対する一般式を考えることが難しくなってしまっている。
ここで「マスが漏れなく埋まっていれば総和を一般的に考えやすくなる」わけであるが、とはいえ慣れていないとそのことに実感がわかないかもしれない。
ということで、次のように表に空っぽのマスが一つも無い場合を実際に考えていこう。
ということで、次のように表に空っぽのマスが一つも無い場合を実際に考えていこう。
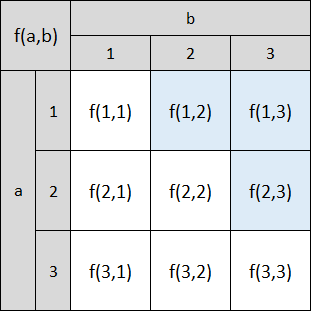
虫食いがなかった時と比べて何が嬉しいのかといえば、「どのマスを飛ばす必要があるのかを心配する必要がない」ということである。
今「この表内の値を全て足し合わせること」を考えてみると、マスを全て埋めたことによってそれは
1. 一行ずつ総和を先に処理してしまう
2. 各行の総和を全て足し合わせる
というたった2つの単純なステップを踏むことで実現できる。
1. 一行ずつ総和を先に処理してしまう
2. 各行の総和を全て足し合わせる
というたった2つの単純なステップを踏むことで実現できる。
まず第一歩として、1行目の総和は
\[
f(1,1)+f(1,2)+f(1,3) = \sum_{b=1}^{3} f(1,b)
\]
同様に2行目、3行目についても
\[
\begin{align}
f(2,1)+f(2,2)+f(2,3) &= \sum_{b=1}^{3} f(2,b) \\
f(3,1)+f(3,2)+f(3,3) &= \sum_{b=1}^{3} f(3,b) \\
\end{align}
\]
つまり一般に、\(a\) 行目の総和は
\[
f(a,1)+f(a,2)+f(a,3) = \sum_{b=1}^{3} f(a,b)
\]
という形で表せることがわかる。
ここでその \(a\) 行目の総和を \(R_a\) と置くと、上の表のすべてのマス内の値の総和 \(A_3\) は、各行の総和を全ての行にわたって足し合わせればよいので、
\[
\begin{align}
A_3 &= R_1 + R_2 + R_3 \\
&= \sum_{a=1}^{3} R_a \\
&= \sum_{a=1}^{3} \left( \sum_{b=1}^{3} f(a,b) \right) \\
\end{align}
\]
である。
(もちろん逆に各列の総和を全ての列にわたって足し合わせても問題ない)
(もちろん逆に各列の総和を全ての列にわたって足し合わせても問題ない)
このように「どのマスを飛ばす必要があるのか」という問題を一旦無視して (つまり余計な項を一旦追加して) マスを全て埋めることで、知っている公式が適用できそうな集合の使われていない総和の形で記述できることになる。
ここで、#3 の問題に戻る。
つまり「関数 \(f\) がどういった良い性質を持っているのか?」という問題である。
つまり「関数 \(f\) がどういった良い性質を持っているのか?」という問題である。
一つ目の表を見て気付いたかもしれないが、和を取られる項というのは行列でいうところの「非対角成分」の一方にまとまって並んでいる。
見やすいように再度同じ表を再び置いておく。

つまり、もしもこの関数が対称性
\[
f(a,b) = f(b,a)
\]
という性質を満たしていれば、その時点で \(A_3\) は「\(S_3\) の2倍に、対角成分に位置する項 \(f(1,1)\), \(f(2,2)\), \(f(3,3)\) を全て足し合わせたものである」ということが直ちにわかることになる。
数式で表せば、
数式で表せば、
\[
A_3 = 2S_3 + \sum_{a=1}^{3} f(a,a)
\]
ちなみに、反対称性
\[
f(a,b) = -f(b,a)
\]
である場合は、非対角成分同士が互いにすべて打ち消しあうことになるので単に対角成分の和となってしまい、その和から非対角部分の和の値を復元することは難しい。
そして \(f\) は都合のいいことに対称性を満たしている。
一応確認しておくと
\[
\begin{align}
f(a,b) &= (a-b)^2 \\
&= ((-1)(b-a))^2 \\
&= (-1)^2(b-a)^2 \\
&= (b-a)^2 \\
&= f(b,a) \\
\end{align}
\]
加えて、対角成分に位置するマスの中にいる \(f(1,1)\), \(f(2,2)\), \(f(3,3)\) は全て零となる。
一応確認しておくと
\[
\begin{align}
f(a,a) &= (a-a)^2 \\
&= 0^2 \\
&= 0 \\
\end{align}
\]
これらのことを踏まえて、表の値を書き直すと
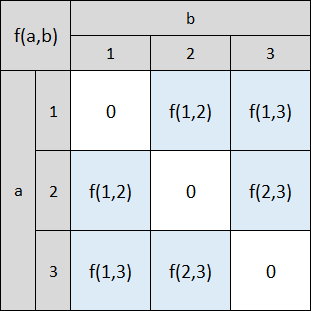
である。
これを見ればこの表の全ての値を足し合わせた値である \(A_3\) が
\[
A_3 = 2S_3
\]
であることが計算するまでもなくわかるだろう。
つまり最初は「右上の青いマスの中の値だけを足すこと」を考えていたために、公式を使えそうな形にもっていくことができず行き詰ってしまっていたわけであるが、一見無駄な作業であるように見える「余計な項も含めた全てのマスの値をまとめて全部足し合わせしまった値 \(A_3\) を求めること」が間接的には「\(S_3\) を求めること」に繋がることがわかったわけである。
余談
「必要なものだけで考えようとすると難しくなるけど、余計なものを追加して考えることで簡単になる」というのに変な感じがするかもしれないが数学ではよくあることである。
例えば、三角関数に関する恒等式は、虚軸という一見余計に見えるものを追加して複素平面に拡張して考えることで簡単に導出できるようになったり、ベクトルのクロス積周りの恒等式に関しても Levi-Civita の記号 \(\varepsilon_{ijk}\) を使って考えることで導出が容易になったりする。
他にも、複素解析の道具を使って実積分の値を発見するというのも、実数の世界の中にいるだけでは全くわからなかったことが、複素数の世界に広げてみるとわかるようになってしまうという意味では似たようなものではないだろうか。
他にも、複素解析の道具を使って実積分の値を発見するというのも、実数の世界の中にいるだけでは全くわからなかったことが、複素数の世界に広げてみるとわかるようになってしまうという意味では似たようなものではないだろうか。
ここまでくれば、あとは単純である。今まで \(n=3\) の場合しか考えてなかったが、\(n=3\) に限らず一般の \(n\) に対しても
\[
\begin{align}
A_n &= 2S_n\\
\end{align}
\]
が成り立つ。
但し、
但し、
\[
\begin{align}
A_n &= \sum_{a=1}^{n} \left( \sum_{b=1}^{n} f(a,b) \right) \\
\end{align}
\]
である。(3×3 のマスを n×n に一般化したバージョン)
\(S_n\) について解くと
\[
\begin{align}
S_n &= \frac{1}{2}A_n\\
\end{align}
\]
ということである。
\(A_n\) を求める一般式が求まれば \(S_n\) もそれから求められることが分かったので、とりあえず \(A_n\) を求める式を整理してしまう。
\[
\begin{align}
A_n &= \sum_{a=1}^{n} \left( \sum_{b=1}^{n} f(a,b) \right) \\
&= \sum_{a=1}^{n} \left( \sum_{b=1}^{n} (a-b)^2 \right) \\
&= \sum_{a=1}^{n} \left( \sum_{b=1}^{n} \left( a^2 - 2ab + b^2 \right) \right) \\
&= \sum_{a=1}^{n} \left( \left( \sum_{b=1}^{n} a^2 \right) - \left( \sum_{b=1}^{n} 2ab \right) + \left( \sum_{b=1}^{n} b^2 \right) \right) \\
&= \sum_{a=1}^{n} \left( \left(a^2 \sum_{b=1}^{n} 1 \right) - \left( 2a \sum_{b=1}^{n} b \right) + \left( \sum_{b=1}^{n} b^2 \right) \right) \\
&= \sum_{a=1}^{n} \left( \left(a^2 \sum_{c=1}^{n} 1 \right) - \left( 2a \sum_{c=1}^{n} c \right) + \left( \sum_{c=1}^{n} c^2 \right) \right) \\
\end{align}
\]
ここで、
\[
\begin{align}
\sum_{c=1}^{n} 1 &= n \\
\end{align}
\]
より (1 を \(n\) 回足し合わせる、つまり「\(1\times n = n\)」)
\[
\begin{align}
A_n &= \sum_{a=1}^{n} \left( \left(a^2 \sum_{c=1}^{n} 1 \right) - \left( 2a \sum_{c=1}^{n} c \right) + \left( \sum_{c=1}^{n} c^2 \right) \right) \\
&= \sum_{a=1}^{n} \left( \left(a^2\cdot n \right) - \left( 2a \sum_{c=1}^{n} c \right) + \left( \sum_{c=1}^{n} c^2 \right) \right) \\
&= \sum_{a=1}^{n} \left(a^2\cdot n \right) - \sum_{a=1}^{n} \left( 2a \left( \sum_{c=1}^{n} c \right) \right) + \sum_{a=1}^{n} \left( \sum_{c=1}^{n} c^2 \right) \\
&= n \cdot \left(\sum_{a=1}^{n} a^2 \right) - \left( \sum_{c=1}^{n} c \right)\cdot \left( \sum_{a=1}^{n} 2a \right) + \left(\sum_{c=1}^{n} c^2 \right)\cdot\left(\sum_{a=1}^{n} 1 \right) \\
&= n \cdot \left(\sum_{a=1}^{n} a^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)\cdot \left( \sum_{a=1}^{n} a \right) + \left(\sum_{c=1}^{n} c^2 \right)\cdot\left(\sum_{a=1}^{n} 1 \right) \\
&= n \cdot \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)\cdot \left( \sum_{c=1}^{n} c \right) + \left(\sum_{c=1}^{n} c^2 \right)\cdot\left(\sum_{c=1}^{n} 1 \right) \\
&= n \cdot \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)^2 + \left(\sum_{c=1}^{n} c^2 \right)\cdot\left(\sum_{c=1}^{n} 1 \right) \\
&= n \cdot \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)^2 + \left(\sum_{c=1}^{n} c^2 \right)\cdot n \\
&= n \cdot \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)^2 + n \cdot \left(\sum_{c=1}^{n} c^2 \right) \\
&= 2n \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)^2\\
\end{align}
\]
ここで、
■ 1つ目の重要な式
■ 1つ目の重要な式
\[
\begin{align}
\sum_{c=1}^{n} c = \frac{n(n+1)}{2}
\end{align}
\]
■ 2つ目の重要な式
\[
\begin{align}
\sum_{c=1}^{n} c^2 = \frac{n(n+1)(2n+1)}{6}
\end{align}
\]
を使うと
\[
\begin{align}
A_n &= 2n \left(\sum_{c=1}^{n} c^2 \right) - 2 \left( \sum_{c=1}^{n} c \right)^2\\
&= 2n \left(\frac{n(n+1)(2n+1)}{6} \right) - 2 \left( \frac{n(n+1)}{2} \right)^2
\end{align}
\]
即ち、
\[
\begin{align}
S_n &= \frac{1}{2} A_n\\
&= \frac{1}{2} \left( 2n \left(\frac{n(n+1)(2n+1)}{6} \right) - 2 \left( \frac{n(n+1)}{2} \right)^2 \right)\\
&= n \left(\frac{n(n+1)(2n+1)}{6} \right) - \left( \frac{n(n+1)}{2} \right)^2\\
&= \frac{n^2(n+1)(2n+1)}{6} - \frac{n^2(n+1)^2}{4} \\
\end{align}
\]
よって答えは、
\[
\begin{align}
S_n &= \frac{n^2(n+1)(2n+1)}{6} - \frac{n^2(n+1)^2}{4} \\
&= \frac{n^2(n^2-1)}{12}
\end{align}
\]
検算用に \(n=1,2,3,4,5\) について具体的に計算してみると、
\[
\begin{align}
S_1 &= 0 \\
S_2 &= 1 \\
S_3 &= 6 \\
S_4 &= 20 \\
S_5 &= 50 \\
\end{align}
\]
補足
ここに解説は載っているけど、ここでも一応なぜ
\[
\begin{align}
\sum_{c=1}^{n} c^2 = \frac{n(n+1)(2n+1)}{6}
\end{align}
\]
が成り立つのかをざっと補足。
\[
\begin{align}
(k-1)^3 &= k^3 - 3k^2 + 3k - 1 \\
k^3 - (k-1)^3 &= 3k^2 - 3k + 1 \\
\end{align}
\]
つまり、
\[
\begin{align}
\sum_{k=1}^{n}(k^3 - (k-1)^3) &= \sum_{k=1}^{n}(3k^2 - 3k + 1) \\
\end{align}
\]
ここで
\[
\begin{align}
左辺 &= \sum_{k=1}^{n}(k^3 - (k-1)^3) \\
&= (1^3 - (1-1)^3) + (2^3 - (2-1)^3) + \cdots + ((n-1)^3 - ((n-1)-1)^3) + (n^3 - (n-1)^3) \\
&= (1^3 - 0^3) + (2^3 - 1^3) + \cdots + ((n-1)^3 - (n-2)^3) + (n^3 - (n-1)^3) \\
&= ((-0^3) + 1^3) + ((-1^3) + 2^3) + \cdots + ((-(n-2)^3) + (n-1)^3) + ((-(n-1)^3) + n^3) \\
&= (-0^3) + 1^3 + (-1^3) + 2^3 + \cdots + (-(n-2)^3) + (n-1)^3 + (-(n-1)^3) + n^3 \\
&= (-0^3) + (1^3 + (-1^3)) + (2^3 + (-2^3)) + \cdots + ((n-2)^3 + (-(n-2)^3)) + ((n-1)^3 + (-(n-1)^3)) + n^3 \\
&= 0+ 0 + 0 + \cdots + 0 + 0 + n^3 \\
&= n^3 \\
\end{align}
\]
となる。よって
\[
\begin{align}
\sum_{k=1}^{n}(k^3 - (k-1)^3) &= \sum_{k=1}^{n}(3k^2 - 3k + 1) \\
n^3 &= \left(\left(\sum_{k=1}^{n} 3k^2 \right) - \left(\sum_{k=1}^{n} 3k \right) + \left(\sum_{k=1}^{n} 1 \right)\right) \\
-\left(\sum_{k=1}^{n} 3k^2 \right) &= -n^3 - \left(\sum_{k=1}^{n} 3k \right) + \left(\sum_{k=1}^{n} 1 \right) \\
\left(\sum_{k=1}^{n} 3k^2 \right) &= n^3 + \left(\sum_{k=1}^{n} 3k \right) - \left(\sum_{k=1}^{n} 1 \right) \\
3\left(\sum_{k=1}^{n} k^2 \right) &= n^3 + 3\left(\sum_{k=1}^{n} k \right) - \left(\sum_{k=1}^{n} 1 \right) \\
3\left(\sum_{k=1}^{n} k^2 \right) &= n^3 + 3\left(\frac{n(n+1)}{2} \right) - n \\
3\left(\sum_{k=1}^{n} k^2 \right) &= n^3 + 3\frac{n(n+1)}{2} - n \\
3\left(\sum_{k=1}^{n} k^2 \right) &= \frac{2n^3 + 3n(n+1) - 2n}{2} \\
3\left(\sum_{k=1}^{n} k^2 \right) &= \frac{n(2n^2 + 3(n+1) - 2)}{2} \\
3\left(\sum_{k=1}^{n} k^2 \right) &= \frac{n(2n^2 + 3n+3 - 2)}{2} \\
3\left(\sum_{k=1}^{n} k^2 \right) &= \frac{n(2n^2 + 3n + 1)}{2} \\
\end{align}
\]
わざわざ因数分解する必要はないけど、たすき掛けで
\[
\begin{align}
3\left(\sum_{k=1}^{n} k^2 \right) &= \frac{n(2n+1)(n+1)}{2} \\
\left(\sum_{k=1}^{n} k^2 \right) &= \frac{n(2n+1)(n+1)}{6} \\
\end{align}
\]
おしまい。
ちなみに、この公式を求めるパターンは
\[
\begin{align}
\left(\sum_{k=1}^{n} k^3 \right) \\
\end{align}
\]
や
\[
\begin{align}
\left(\sum_{k=1}^{n} k^4 \right) \\
\end{align}
\]
に対しても有効なので、誘導方法を覚えておくといいかも。
以下、因数分解を力技で行うくだりなので、因数分解ばっちりであれば読まなくても問題なし。
(二次の多項式に対しては万能なので、一応流れを覚えていても損はないかも)
(二次の多項式に対しては万能なので、一応流れを覚えていても損はないかも)
\[
\begin{align}
2n^2 + 3n + 1 &= 0 \\
n &= \frac{-3 \pm \sqrt{3^2 - 4\cdot2\cdot 1}}{2\cdot 2} \\
n &= \frac{-3 \pm 1}{4} \\
\end{align}
\]
よって、\(\alpha\) を未知数とすると
\[
\begin{align}
2n^2 + 3n + 1 &= \alpha \cdot ((n-\frac{-3 + 1}{4})(n-\frac{-3 - 1}{4})) \\
2n^2 + 3n + 1 &= \alpha \cdot ((n-\frac{-2}{4})(n-\frac{-4}{4})) \\
2n^2 + 3n + 1 &= \alpha \cdot ((n+\frac{1}{2})(n+1)) \\
2n^2 + 3n + 1 &= \alpha \cdot (n^2+\frac{3}{2}n+\frac{1}{2}) \\
2n^2 + 3n + 1 &= \alpha n^2+ \frac{3}{2}\alpha n+ \frac{1}{2}\alpha \\
\end{align}
\]
係数同士を比較すると、\(\alpha\) は
\[
\begin{align}
2 &= \alpha \\
3 &= \frac{3}{2}\alpha \\
1 &= \frac{1}{2}\alpha \\
\end{align}
\]
の3つを全て満たす数でなければならないが、それは明らかに
\[
\alpha = 2
\]
(ネタバレをしてしまえば、こんな回りくどいことをしなくても \(\alpha\) は2次の項の係数として直ちにわかる)
よって
\[
\begin{align}
& 2n^2 + 3n + 1\\
=& 2 \cdot ((n-\frac{-3 + 1}{4})(n-\frac{-3 - 1}{4})) \\
=& 2 \cdot ((n+\frac{1}{2})(n+1)) \\
=& (2n+2\cdot\frac{1}{2})(n+1) \\
=& (2n+1)(n+1) \\
\end{align}
\]
無意味な因数分解終了。
タグ一覧:
