雑記帳
階乗の不等式に関する問題
問題3
(1) \(y = \log x\) のグラフを用いて、2以上の自然数 \(k\) に対して次の不等式が成り立つことを示せ。
\[
\int_{k-1}^{k} \log x \: dx < \log k < \int_{k}^{k+1} \log x \: dx
\]
(2) \(2\le n\) について
\[
e\left( \frac{n}{e} \right)^2 < n! < \frac{e^2}{4}\left( \frac{n+1}{e} \right)^{n+1}
\]
が成り立つことを示せ。
<未完成>
(1) の解答例
(1) の解答例
まずわかりやすいように、次のような関数 \(S_{-}\), \(S_{+}\) を定義する。
\[
\begin{align}
S_{-}(k) &:= \int_{k-1}^{k} \log x \: dx \\
S_{+}(k) &:= \int_{k}^{k+1} \log x \: dx \\
\end{align}
\]
但し、\(k\) は 2以上の自然数であるとする。
余談
後々のことを考えて用語を紹介すると、その関数の変数に代入されることになる値全体となる「2以上の自然数」というのは、それらの関数 \(S_{-}\), \(S_{+}\) のドメイン (domain) あるいは定義域と呼ばれる。
関数というのは、現代数学を記述する集合論 (set theory) とはまた異なるもう一つの基礎言語として認識されつつある圏論 (category theory) において、非常に重要な位置付けのされる概念となり、その扱いに慣れておくことは今後抽象度の高い数学を理解するうえで欠かせないものとなってくる。
関数というのは、現代数学を記述する集合論 (set theory) とはまた異なるもう一つの基礎言語として認識されつつある圏論 (category theory) において、非常に重要な位置付けのされる概念となり、その扱いに慣れておくことは今後抽象度の高い数学を理解するうえで欠かせないものとなってくる。
まずなんの意図があってこのような関数を定義したのかを理解するために、グラフ上でのそれら関数の立ち位置を明らかにする。

上の図を見ればわかっていただけると思うが、関数 \(S_{-}\), \(S_{+}\) の意味というのは
■ \(S_{-}\)
2以上の自然数 \(k\) に対して、
・\(x\) 軸上にある \(x=k\) の点を出発点に鉛直方向に引いた直線
・\(x=k\) から1だけ戻った位置 (つまり \(x=k-1\)) を出発点として同様に鉛直方向に引いた直線
・\(y=\log x\)
・\(x\) 軸
の4つの線によって囲まれてできた図形の面積を求める関数。
2以上の自然数 \(k\) に対して、
・\(x\) 軸上にある \(x=k\) の点を出発点に鉛直方向に引いた直線
・\(x=k\) から1だけ戻った位置 (つまり \(x=k-1\)) を出発点として同様に鉛直方向に引いた直線
・\(y=\log x\)
・\(x\) 軸
の4つの線によって囲まれてできた図形の面積を求める関数。
■ \(S_{+}\)
2以上の自然数 \(k\) に対して、
・\(x\) 軸上にある \(x=k\) の点を出発点に鉛直方向に引いた直線
・\(x=k\) から1だけ進んだ位置 (つまり \(x=k+1\)) を出発点として同様に鉛直方向に引いた直線
・\(y=\log x\)
・\(x\) 軸
の4つの線によって囲まれてできた図形の面積を求める関数。
2以上の自然数 \(k\) に対して、
・\(x\) 軸上にある \(x=k\) の点を出発点に鉛直方向に引いた直線
・\(x=k\) から1だけ進んだ位置 (つまり \(x=k+1\)) を出発点として同様に鉛直方向に引いた直線
・\(y=\log x\)
・\(x\) 軸
の4つの線によって囲まれてできた図形の面積を求める関数。
ここで、先ほど定義した関数を使って設問 (1) の不等式を見やすく書き換えてみよう。
\[
S_{-}(k) < \log k < S_{+}(k)
\]
ここで、一つ違和感に気付いていただきたい。
冷静にこの式を見てみると、まず \(S_{-}(k)\) と \(S_{+}(k)\) がそれぞれ「(符号付き) 面積」という面の広さに対する値であるのに対して、真ん中に居座っている \(\log k\) さんは一見するとそういった「符号付き面積」ではなく特別な意味の与えられてない単なる抽象的な「数字 (値)」にしか見えない。
冷静にこの式を見てみると、まず \(S_{-}(k)\) と \(S_{+}(k)\) がそれぞれ「(符号付き) 面積」という面の広さに対する値であるのに対して、真ん中に居座っている \(\log k\) さんは一見するとそういった「符号付き面積」ではなく特別な意味の与えられてない単なる抽象的な「数字 (値)」にしか見えない。
具体例を挙げさせてもらうと、例えば「\(100[m^2]\) のグラウンド」と「\(400[m^2]\) のグラウンド」という同じく面積という意味を持った2つの値が与えられたとき、「この時どちらのグラウンドが広いか」という問題には違和感は抱かないことと思う。
一方で、「\(100[m^2]\) のグラウンド」と「\(100[m]\) の高さを持つビル」に対して、「どちらが大きいか」と言われたら「はい?」と反応してしまうのではないだろうか。
今考えている問題の場合は、\(\log k\) というのがグラフ上で見たときに「\(S_{-}(k)\) と \(S_{+}(k)\)で求められることになる2つの図形で挟まれた直線の長さ」として見えてしまうため、言ってしまえば「(敷地の広さのような) 面積の次元を持つ量」と「(ビルの高さのような)長さの次元を持つ量」(あるいは「アスペクト比のような無次元量」)とを比較しようとしている風に見えてしまうわけである。
一方で、「\(100[m^2]\) のグラウンド」と「\(100[m]\) の高さを持つビル」に対して、「どちらが大きいか」と言われたら「はい?」と反応してしまうのではないだろうか。
今考えている問題の場合は、\(\log k\) というのがグラフ上で見たときに「\(S_{-}(k)\) と \(S_{+}(k)\)で求められることになる2つの図形で挟まれた直線の長さ」として見えてしまうため、言ってしまえば「(敷地の広さのような) 面積の次元を持つ量」と「(ビルの高さのような)長さの次元を持つ量」(あるいは「アスペクト比のような無次元量」)とを比較しようとしている風に見えてしまうわけである。
つまり何が言いたいのかといえば、長さの次元を持つ量に見える「\(\log k\) さん」を、 \(S_{-}(k)\) と \(S_{+}(k)\) がいる土俵である「面積の次元を持つ量」という土俵に持って行って考えることができればうれしいのである。
でもどうすればよいのかと思うかもしれないが、落ち着いて考えれば何もそんな大層なことをする必要は全くない。
単に、\(\log k\) を
単に、\(\log k\) を
\[
\log k = \log k \times 1
\]
というように「縦の長さ \(\log k\)、横の長さ \(1\) の矩形 (rectangle) の面積」と捉えてしまえばよいのである。
余談
こういった「(矩形の面積の値をはじめとする) ある構造に対して与えられる値」ではなく「(その面積の値を求めるターゲットとなる矩形それ自体のような) 背後に溶け込んで見えづらくなりがちな構造」をうまく認識して明示化することは重要である。
例えば空間ベクトルというのは、それぞれ「3つの実数の組」として表現されるが、その「3つの実数値」という具体的な数字には直接注目せずに、その「実数の組の全体と、その全体に対して定義される特定の条件を満たす演算たちが織りなす線形空間と呼ばれる数学的構造」という各々の空間ベクトルの成分表示を個別に見ていた時には認識しづらかった構造の方に注目をして議論を進めていくこともできる。
この例の場合で言えば単に「不必要な具体性に惑わされない一般論を進めていくため」という消極的な理由に受け取れてしまうが、実はこういった抽象論は「数字を使った図形の表現」への依存なしに幾何的な対象を統括的に考察していくことも可能にする。
例えば空間ベクトルというのは、それぞれ「3つの実数の組」として表現されるが、その「3つの実数値」という具体的な数字には直接注目せずに、その「実数の組の全体と、その全体に対して定義される特定の条件を満たす演算たちが織りなす線形空間と呼ばれる数学的構造」という各々の空間ベクトルの成分表示を個別に見ていた時には認識しづらかった構造の方に注目をして議論を進めていくこともできる。
この例の場合で言えば単に「不必要な具体性に惑わされない一般論を進めていくため」という消極的な理由に受け取れてしまうが、実はこういった抽象論は「数字を使った図形の表現」への依存なしに幾何的な対象を統括的に考察していくことも可能にする。
例として「大きさと方向 (姿勢) を持った n次元要素」というものは、「大きさと方向を持った 1次元要素 (つまり有向線分である"矢印"として図示される空間ベクトル)」のなす線形空間 \(V\) から構成される「n次外冪 \(\bigwedge^n V\)」と呼ばれる新たな線形空間の要素として具体的な数字を使った表現への還元をすることなしに直接取り扱っていくことができるのである。
一貫性を持たせるために、この \(k\) に対して、その矩形の面積「\(\log k \times 1\)」を求める関数 \(S_0\) を定義する。
\[
S_0(k) := \log k \times 1
\]
■ \(S_0\)
2以上の自然数 \(k\) に対して、縦の長さ \(\log k\)、横の長さ \(1\) の矩形 (rectangle) の面積を求める関数。
2以上の自然数 \(k\) に対して、縦の長さ \(\log k\)、横の長さ \(1\) の矩形 (rectangle) の面積を求める関数。
この関数を用いて再度、設問の不等式を書き換えてみると次のようになる。
\[
S_{-}(k) < S_0(k) < S_{+}(k)
\]
ここで わかりやすいように \(S_0(k)\) により求められる矩形を実際にグラフ上に置いて見てみよう。
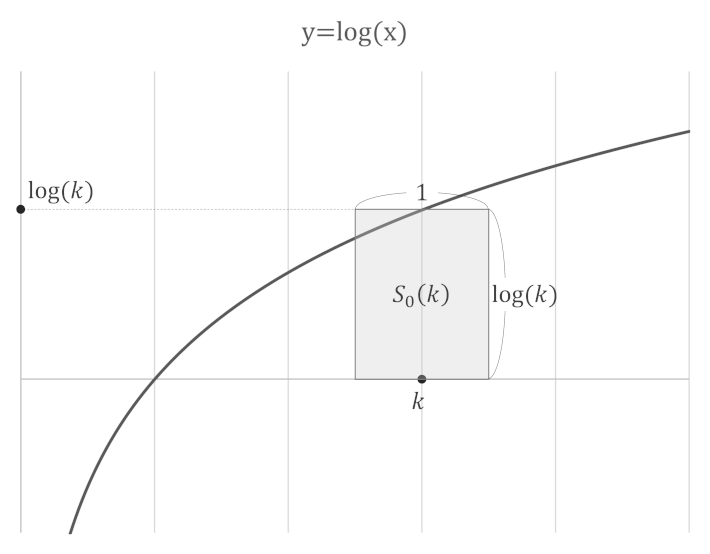
ポイントとなるのは、「横の長さ \(1\)」というのが \(S_{-}(k)\) と \(S_{+}(k)\) に対しても共通であるということである。
となれば、実際にそれらを重ね合わせてみればその大小関係は敢えて考えるまでもなく視覚的に明らかになってしまうわけである。
となれば、実際にそれらを重ね合わせてみればその大小関係は敢えて考えるまでもなく視覚的に明らかになってしまうわけである。

(2) の解答例
設問 (1) を解かせた上で、この問題が問われたということは、設問 (1) が 設問 (2) を解く手がかりになっている場合が多い。
ということでまずは素直に「グラフ上の面積」の大小関係をうまく使うことが、その不等式を導くことに繋がるのであろうと考えてしまう。
ということでまずは素直に「グラフ上の面積」の大小関係をうまく使うことが、その不等式を導くことに繋がるのであろうと考えてしまう。
第一に思うのは「階乗は何処からやってくるのか」という疑問ではないだろうか。
この疑問を解消する上で重要となってくるのは、対数関数が「積を和に変えたり、和を積に変えたりできる」という特徴的な性質を持っているということである。
(問われている不等式の両側に「ネイピア数 \(e\)」が含まれているということからも、その不等式に行きつくまでに「対数関数を打ち消す操作」を使っているかもしれない、即ちどこかしらで対数が使われているのだろうという漠然とした予想がつくことと思う。)
(問われている不等式の両側に「ネイピア数 \(e\)」が含まれているということからも、その不等式に行きつくまでに「対数関数を打ち消す操作」を使っているかもしれない、即ちどこかしらで対数が使われているのだろうという漠然とした予想がつくことと思う。)
具体的には
\[
\log(x\cdot y) = \log x + \log y
\]
という性質である。
つまり、\(\log k\) に対する総和から次のようにして階乗の形を作ることができるわけである。
\[
\begin{align}
\sum_{k=1}^{n} \log k &= \log 1 + \log 2 + \cdots + \log(n-1) + \log n \\
&= \log(1\times 2\times\cdots \times(n-1)\times n) \\
&= \log(n!) \\
\end{align}
\]
ここで今の設問において、\(k=2\) 以上の自然数を考えているため、出発点が \(k=1\) であると都合が悪いのであるが、\(\log 1 = 0\) であるので次のように、\(k=2\) から始めても全く同様に「階乗の対数」の形を作ることができる。
\[
\begin{align}
\sum_{k=2}^{n} \log k &= \log 2 + \cdots + \log(n-1) + \log n \\
&= 0 + \log 2 + \cdots + \log(n-1) + \log n \\
&= \log 1 + \log 2 + \cdots + \log(n-1) + \log n \\
&= \log(1\times 2\times\cdots \times(n-1)\times n) \\
&= \log(n!) \\
\end{align}
\]
blah
\[
\begin{align}
S_{-}(k) &<& S_0(k) &<&& S_{+}(k) \\
\sum_{k=2}^{n} S_{-}(k) &<& \sum_{k=2}^{n} S_0(k) &<&& \sum_{k=2}^{n} S_{+}(k) \\
\int_{1}^{n} \log x \: dx &<& \log(n!) &<&& \int_{2}^{n+1} \log x \: dx \\
{\Big[x(\log x - 1) \Big]}_{1}^{n} &<& \log(n!) &<&& {\Big[x(\log x - 1) \Big]}_{2}^{n+1} \\
\log(n^n)+(1-n) &<& \log(n!) &<&& \log((n+1)^{n+1})+(1-n)+\log(4^{-1}) \\
\end{align}
\]
\(f(x) = e^x\) で定まる関数 \(f\) は (実数の世界の中では) 単調増加であるので、
\[
a < b
\]
が満たされる \(a,b\) に対して
\[
f(a) < f(b)
\]
が成り立つ。
\[
\begin{align}
\log(n^n)+(1-n) &<& \log(n!) &<&& \log((n+1)^{n+1})+(1-n)+\log(4^{-1}) \\
e^{\log(n^n)+(1-n)} &<& e^{\log(n!)} &<&& e^{\log((n+1)^{n+1})+(1-n)+\log(4^{-1})} \\
n^n\cdot e^{(1-n)} &<& n! &<&& (n+1)^{n+1}\cdot e^{(1-n)}\cdot 4^{-1} \\
e\cdot \left( \frac{n}{e} \right)^n &<& n! &<&& (n+1)^{n+1}\cdot e^{(1-(n+1)+1)}\cdot 4^{-1} \\
e\cdot \left( \frac{n}{e} \right)^n &<& n! &<&& \frac{e^2}{4}\left( \frac{n+1}{e} \right)^{n+1} \\
\end{align}
\]
タグ一覧:
