雑記帳
Haskell でレイトレーシングのチュートリアルを追いかける その12 - 金属 (修正版)
修正版の作成の続きとして、セクション9の内容のやり直しを行った。
出力画像を眺めてみたところ、金属のトーラスの内側に数値解析でやっていた時には無かったリング状の色付けが発生しているけど、こちらの方が正しいということでいいのかな。
最初は「色が不連続に変化しているのはおかしいのかな」なんてことも思ったけど、「反射したレイが自身に再び衝突するか衝突しないかの瀬戸際となる場所」では色付けは不連続になるだろうし、こちらの方が理に適っていると考えてよさそうだろうなんてことを勝手に思ってしまっているけど...
カメラ周りの調整が出来れば、この辺も自然な形で見えてくるのだろうか。(実際、カメラの調整を行っていない今の状態だと、右奥のトーラスの形すらなんだか不自然に感じる)
コードの実行結果
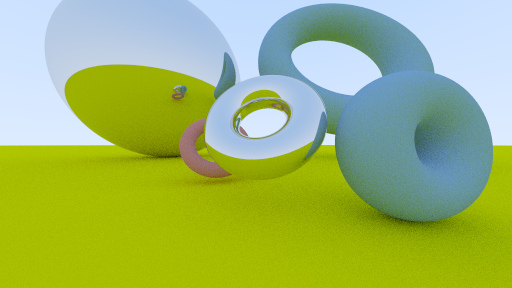
ソースコード
{-# LANGUAGE TypeOperators #-}
module Main where
import Data.Complex
import Control.Monad.Fix
import Control.Lens
import System.Random
import Linear.Vector
import Linear.Metric
import Linear.V3
-- https://raytracing.github.io/books/RayTracingInOneWeekend.html
-- section 9-5 A Scene with Metal Spheres with Haskell!!
main :: IO ()
main = do
let
-- Image
aspect_ratio = 16.0 / 9
image_width = 512
image_height = round $ fromIntegral image_width / aspect_ratio
samples_per_pixel = 100
max_depth = 100
-- World
material_ground = make_shared $ MAT_Lambertian {albedo_Lamb = V3 0.8 0.8 0.0}
material_red = make_shared $ MAT_Lambertian {albedo_Lamb = V3 0.7 0.3 0.3}
material_blue = make_shared $ MAT_Lambertian {albedo_Lamb = V3 0.3 0.5 0.7}
material_silver = make_shared $ MAT_Metal {albedo_Metal = V3 0.8 0.8 0.8}
material_gold = make_shared $ MAT_Metal {albedo_Metal = V3 0.8 0.6 0.2}
world = []
--`add` RT_Sphere{center = V3 0.0 (-1.0) 0.0, radius = 0.5, mat_Sphere = material_center}
--`add` RT_Sphere{center = V3 (-0.95) (-1.0) 0.0, radius = 0.5, mat_Sphere = material_left}
--`add` RT_Sphere{center = V3 1.05 (-1.0) 0.0, radius = 0.5, mat_Sphere = material_right}
`add` RT_Torus{
centerOfTorus = V3 (-0.55) (-2.1) 0.0,
majorRadius = 0.4,
minorRadius = 0.1,
orientationOfTorus = normalize $ V3 0.5 1.5 1.0,
mat_Torus = material_red
}
`add` RT_Torus{
centerOfTorus = V3 1.05 (-1.0) 0.0,
majorRadius = 0.3,
minorRadius = 0.2,
orientationOfTorus = normalize $ V3 (-0.5) (-3) (-0.2),
mat_Torus = material_blue
}
`add` RT_Sphere{center = V3 (-3.51) (-5.9) 2.4, radius = 2.9, mat_Sphere = material_silver}
`add` RT_Torus{
centerOfTorus = V3 3.51 (-6.1) 3.5,
majorRadius = 2.7,
minorRadius = 0.7,
orientationOfTorus = normalize $ V3 0 1 0.4,
mat_Torus = material_blue
}
`add` RT_Torus{
centerOfTorus = V3 0.05 (-1.2) 0.2,
majorRadius = 0.35,
minorRadius = 0.15,
orientationOfTorus = normalize $ V3 (-0.5) 1.9 1.2,
mat_Torus = material_silver
}
`add` RT_Sphere{center = V3 0 (-1) (-100000.5), radius = 100000, mat_Sphere = material_ground}
-- Camera
camera = Camera {
viewport_height = 2.0,
viewport_width = aspect_ratio * viewport_height camera,
focal_length = 1.0,
origin = zero,
horizontal = viewport_width camera *^ unit _x,
vertical = viewport_height camera *^ unit _z,
lower_left_corner =
origin camera - horizontal camera ^/2 - vertical camera ^/2
- focal_length camera *^ unit _y
}
img_data = "P3\n" ++ show image_width ++ " " ++ show image_height ++ "\n255\n"
putStr $ img_data
foldr (>>) (return ()) $ do
let
indices = [image_height - 1, image_height - 2 .. 0] `prod` [0 .. image_width - 1]
seeds = (randomRs (0, 536870912) (mkStdGen 21) :: [Int])
((j,i), seed) <- zip indices seeds
return $ do
let
rnds = myRandoms (2*samples_per_pixel) (mkStdGen seed)
pixcel_color = foldr (+) 0 $ do
s <- [0 .. samples_per_pixel - 1]
let
(randNum1, _) = rnds !! (2*s + 0)
(randNum2, gen2) = rnds !! (2*s + 1)
u = (fromIntegral i + randNum1) / (fromIntegral image_width - 1.0)
v = (fromIntegral j + randNum2) / (fromIntegral image_height - 1.0)
r = get_ray camera (u, v)
return $ ray_color r world max_depth gen2
write_color pixcel_color samples_per_pixel
myRandoms :: RandomGen g => Int -> g -> [(Double,g)]
myRandoms num gen = f(0,[],gen)
where
f = fix $ \rec (i,xs,gen_current) ->
if i < num then
let
x@(next, gen_new) = random gen_current
in
rec (succ i, x:xs, gen_new)
else
xs
data Ray = Ray {
orig :: V3 Double,
dir :: V3 Double
} deriving (Show)
at' :: Ray -> Double -> V3 Double
at' r t = (orig r) + t *^ (dir r)
data Camera = Camera {
viewport_height :: Double,
viewport_width :: Double,
focal_length :: Double,
origin :: V3 Double,
horizontal :: V3 Double,
vertical :: V3 Double,
lower_left_corner :: V3 Double
} deriving (Show)
get_ray :: Camera -> (Double, Double) -> Ray
get_ray this (u, v) =
Ray {
orig = origin this,
dir = lower_left_corner this + u *^ horizontal this + v *^ vertical this - origin this
}
type HittableData = (RT_Sphere + RT_Torus) + RT_Sphere
class Hittable a where
toSum :: a -> HittableData
hit :: a -> Ray -> Double -> Double -> Maybe HitRecord
instance (Hittable a, Hittable b) => Hittable (Either a b) where
toSum = coPair(toSum, toSum)
hit = coPair(hit, hit)
add :: Hittable a => [HittableData] -> a -> [HittableData]
add list obj = (toSum obj) : list
data HitRecord = HitRecord {
p :: V3 Double,
normal :: V3 Double,
mat :: MaterialData,
t :: Double,
front_face :: Bool
} deriving (Show)
set_face_normal :: HitRecord -> Ray -> V3 Double -> HitRecord
set_face_normal this r outward_normal = HitRecord {
p = p this,
normal = if dir r `dot` outward_normal < 0 then outward_normal else -outward_normal,
t = t this,
front_face = (dir r `dot` outward_normal < 0),
mat = mat this
}
hitSomething :: [HittableData] -> Ray -> Double -> Double -> Maybe HitRecord
hitSomething list r t_min t_max =
let
f (list', r', closest_so_far, currentRecord) =
case list' of
x:xs ->
let temp = hit x r' t_min closest_so_far in
case temp of
Just a ->
f $ (xs, r', t a, temp)
Nothing ->
f $ (xs, r', closest_so_far, currentRecord)
[] ->
currentRecord
in
f $ (list, r, t_max, Nothing)
----------------------
-- Hittable Objects --
----------------------
-- Sphere
data RT_Sphere = RT_Sphere {
center :: V3 Double,
radius :: Double,
mat_Sphere :: MaterialData
} deriving (Show)
instance Hittable RT_Sphere where
toSum = inj1 -: inj1
hit obj r t_min t_max =
let
p0 = orig r
c1 = center obj
r1 = radius obj
oc = p0 - c1
a = quadrance (dir r)
half_b = oc `dot` dir r
c = quadrance oc - (radius obj) ^ 2
discriminant = half_b ^ 2 - a*c in
if discriminant > 0 then
let
root = sqrt discriminant
f k =
case k of
x:xs ->
if t_min < x && x < t_max then
return $ set_face_normal HitRecord {
p = at' r x,
normal = zero,
t = x,
front_face = False,
mat = mat_Sphere obj
} r ((at' r x - c1) ^/ r1)
else
f $ xs
[] ->
Nothing
in
f $ [(-half_b - root) / a, (-half_b + root) / a]
else
Nothing
-- Torus
data RT_Torus = RT_Torus {
centerOfTorus :: V3 Double,
majorRadius :: Double,
minorRadius :: Double,
orientationOfTorus :: V3 Double, -- [BEWARB] this pseudo-vector must be normalized
mat_Torus :: MaterialData
} deriving (Show)
instance Hittable RT_Torus where
toSum = inj2 -: inj1
hit obj r t_min t_max =
let
p0 = orig r
a = dir r
a_norm = norm a
c1 = centerOfTorus obj
r1 = majorRadius obj
r2 = minorRadius obj
n = orientationOfTorus obj
s = getIntersection_forTorus (p0,a,c1,r1,r2,n)
oc = p0 - c1
a_sq = quadrance (dir r)
half_b = oc `dot` dir r
c = quadrance oc - (r1 + r2 + 0.01) ^ 2
discriminant = half_b ^ 2 - a_sq*c
in
if discriminant > 0 then
if null s then
Nothing
else
let
k = minimum s
x = at' r k - c1
in
if t_min < k && k < t_max then
return $ set_face_normal HitRecord {
p = c1 + x,
normal = zero,
t = k,
front_face = False,
mat = mat_Torus obj
} r ((x - (r1 *^ (normalize $ x - (n `dot` x) *^ n))) ^/ r2)
else
Nothing
else
Nothing
write_color :: V3 Double -> Int -> IO ()
write_color (V3 r g b) spp =
let
v' = V3 (sqrt $ r / fromIntegral spp) (sqrt $ g / fromIntegral spp) (sqrt $ b / fromIntegral spp)
f = show.floor.(256*).(clamp 0 0.999)
in
putStr $ f(v' ^._x) ++ " " ++ f(v' ^._y) ++ " " ++ f(v' ^._z) ++ "\n"
ray_color :: Ray -> [HittableData] -> Int -> StdGen -> V3 Double
ray_color r objects depth gen =
if depth <= 0 then
zero
else
let
record = hitSomething objects r 0.0001 infinity
in
case record of
Just record' ->
let
(ret, gen1) = scatter (mat record') r record' gen
in
case ret of
Just (scattered, attenuation) ->
attenuation * (ray_color scattered objects (pred depth) gen1)
Nothing ->
zero
Nothing ->
let
unit_direction = normalize $ (dir r)
s = 0.5 * (unit_direction ^._z + 1.0)
in
lerp s (V3 0.5 0.7 1.0) (V3 1.0 1.0 1.0)
--------------------
-- Random numbers --
--------------------
random_in_unit_sphere :: StdGen -> (V3 Double, StdGen)
random_in_unit_sphere gen0 =
let
(rand1,gen1) = randomR (-1, 1) gen0 :: (Double, StdGen)
(rand2,gen2) = randomR (-1, 1) gen1 :: (Double, StdGen)
(rand3,gen3) = randomR (-1, 1) gen2 :: (Double, StdGen)
v = V3 rand1 rand2 rand3
in
if quadrance v >= 1 then
random_in_unit_sphere gen3
else
(v, gen3)
random_unit_vector :: StdGen -> (V3 Double, StdGen)
random_unit_vector gen0 =
let
(a, gen1) = randomR (0, 2*pi) gen0 :: (Double, StdGen)
(z, gen2) = randomR (-1, 1) gen1 :: (Double, StdGen)
r = sqrt $ 1 - z^2
in
(V3 (r*cos(a)) (r*sin(a)) z, gen2)
random_in_hemisphere :: V3 Double -> StdGen -> (V3 Double, StdGen)
random_in_hemisphere normal gen0 =
let
(in_unit_sphere, gen1) = random_in_unit_sphere gen0
in
if in_unit_sphere `dot` normal > 0 then
(in_unit_sphere, gen1)
else
(-in_unit_sphere, gen1)
---------------
-- Utilities --
---------------
infinity :: RealFloat a => a
infinity = encodeFloat (floatRadix 0 - 1) (snd $ floatRange 0)
deg2rad :: Floating a => a -> a
deg2rad degrees = degrees * pi / 180
clamp :: (Ord a, Num a) => a -> a -> a -> a
clamp x y val = (max x).(min y) $ val
reflect :: V3 Double -> V3 Double -> V3 Double
reflect v n = v - (2 * (n `dot` v)) *^ n
near_zero (V3 r1 r2 r3) =
(abs(r1) < s) && (abs(r2) < s) && (abs(r3) < s)
where
s = 1.0E-9
--------------------
-- Material Class --
--------------------
type MaterialData = (MAT_Lambertian + MAT_Metal) + MAT_Lambertian
class Material a where
make_shared :: a -> MaterialData
scatter :: a -> Ray -> HitRecord -> StdGen -> (Maybe (Ray, V3 Double), StdGen)
instance (Material a, Material b) => Material (Either a b) where
make_shared = coPair(make_shared, make_shared)
scatter = coPair(scatter, scatter)
-- Lambertian
data MAT_Lambertian = MAT_Lambertian {
albedo_Lamb :: V3 Double
} deriving (Show)
instance Material MAT_Lambertian where
make_shared = inj1 -: inj1
scatter this r_in record gen =
let
(rand1, gen1) = random_unit_vector gen
scattered_direction =
if near_zero(normal record + rand1) then
normal record
else
normal record + rand1
scattered = Ray{orig = p record, dir = scattered_direction}
attenuation = albedo_Lamb this
in
(Just (scattered, attenuation), gen1)
-- Metal
data MAT_Metal = MAT_Metal {
albedo_Metal :: V3 Double
} deriving (Show)
instance Material MAT_Metal where
make_shared = inj2 -: inj1
scatter this r_in record gen =
let
reflected = reflect (normalize $ dir r_in) (normal record)
scattered = Ray{orig = p record, dir = reflected}
attenuation = albedo_Metal this
in
if (dir scattered `dot` normal record) > 0 then
(Just (scattered, attenuation), gen)
else
(Nothing, gen)
getIntersection_forTorus :: (V3 Double, V3 Double, V3 Double, Double, Double, V3 Double) -> [Double]
getIntersection_forTorus = solveQuarticEq . genCoefficients
genCoefficients (x0,a,c,r1,r2,n) = (b4,b3,b2,b1,b0)
where
d0 = x0 - c
k = (r1^2) - (r2^2)
a_sq = quadrance a
d0_sq = quadrance d0
b4 = a_sq^2
b3 = 4*(d0 `dot` a)*a_sq
b2 = 2*d0_sq*a_sq+4*((d0 `dot` a)^2) + 2*k*a_sq - 4*(r1^2)*a_sq + 4*(r1^2)*(n `dot` a)^2
b1 = 4*d0_sq*(d0 `dot` a)+4*k*(d0 `dot` a) - 8*(r1^2)*(d0 `dot` a) + 8*(r1^2)*(n `dot` d0)*(n `dot` a)
b0 = d0_sq*d0_sq+2*k*d0_sq+k^2 - 4*(r1^2)*d0_sq + 4*(r1^2)*(n `dot` d0)^2
solveQuarticEq (a4,a3,a2,a1,a0) =
let
sol = do
(x_Re :+ x_Im) <- [x1,x2,x3,x4]
if (abs(x_Im) < 1.0E-9) && (1.0E-9 <= x_Re) then
return x_Re
else
[]
in
sol
where
l1 = (toCmp $ k3/4)/sqrt(k4)
l2 = (toCmp $ (cbrt(2)*k5)/(3*a4))/k8 + k8/(toCmp $ 3*cbrt(2)*a4)
l3 = (toCmp $ (a3^2)/(2*a4^2) - (4*a2)/(3*a4)) - l2
k1 = l1 + l3
k2 = -l1 + l3
k3 = -((a3/a4)^3) + (4*a2*a3)/(a4^2) - (8*a1)/a4
k4 = (toCmp $ ((a3/(2*a4))^2) - (2*a2)/(3*a4)) + l2
k5 = a2^2 - 3*a1*a3 + 12*a0*a4
k6 = 2*a2^3 - 9*a1*a2*a3 + 27*a0*a3^2 + 27*a1^2*a4 - 72*a0*a2*a4
k7 = -4*k5^3 + k6^2
k8 = cbrt((toCmp $ k6) + sqrt(toCmp $ k7))
l4 = toCmp $ -a3/(4*a4)
l5 = sqrt(k2)/2
l6 = sqrt(k1)/2
l7 = sqrt(k4)/2
x1 = l4 - l5 - l7
x2 = l4 + l5 - l7
x3 = l4 - l6 + l7
x4 = l4 + l6 + l7
cbrt x = x ** (1/3)
toCmp x = x :+ 0
prod x y = x >>= (\u -> zip (repeat u) y)
(-:) = flip (.)
type (+) a b = Either a b
inj1 :: a -> a + b
inj1 = Left
inj2 :: b -> a + b
inj2 = Right
coPair :: (a1 -> b, a2 -> b) -> (a1 + a2 -> b)
coPair = uncurry eitherタグ一覧:
