雑記帳
Haskell 言語を使った階乗関数の様々な実装例 (Wikipedia の例だけでは物足りない方向け)
Haskell 言語による階乗関数の実装例
このサイトでは圏論を躊躇なく積極的に使用するという方針をとっていることもあり、抽象的な話が多くなってしまっている可能性がある。
ということで、たまには実際に動作する Haskell コードを紹介するという柄にもない具体的なことをしてみる。
以下の5つの縛り付きで階乗関数を実装する例を幾つか紹介。
- 一行完結
- 関数のパターンマッチング禁止 (
fac = ... の形で定義する) - 自己参照禁止 (右辺に fac を登場させてはいけない)
- 定義済み関数として使用するのは Prelude 標準モジュール内の関数のみ (例として挙げるコードが実際に動作することを公式サイト上で簡単に検証できるようにするため。というのも公式サイトでは Prelude 以外の関数たちは基本的に使用できない。)
- let は使用しない (これを許容してしまうと「関数のパターンマッチング禁止」と「自己参照禁止」の縛りが意味をなさなくなってしまう)
余談
2023年1月13日現在、Haskell 公式サイトでは putStrLn や getLine といった IO 関係の関数や値は使用できなくなっている。
Point-free でない定義たち
恐らく最もベーシックな定義
既存の関数から構成せずに、ラムダを使って新たな関数として直接定義してしまったもの。(Point-free でない関数の定義)
fac = (\n -> product [1..n])コードを見ての通り、fac という識別子に
fac という識別子に- 入力 n に対して、「1 から n までの整数を持ったリスト [1..n] を 関数 product に渡すことで得られる数値 product [1..n]」を戻り値として返す関数
を定義付けている。
より具体的に、例えば
fac 5というコードはこの場合
(\n -> product [1..n]) 5であり、もちろん
product [1..5]というように、1から5までの全ての整数の積の結果である 120 が出力として得られる。
余談
プログラミング言語界隈では、このような新たな関数の定義はしばしば「無名関数 (Anonymous function)」による定義と呼ばれるが、数学的には関数というのは「名前が与えられることなしに構成され存在できる (無名である) 概念」として捉えるのが普通である。
通常の自己参照を含んだ定義を与えられた縛りの中で無理やり真似てみたもの
以下の
\[
n! =
\begin{cases}
n \times (n-1)! & n > 0 \\
1 & \text{ otherwise }
\end{cases}
\]
という自然数の階乗の定義に則った実装には、通常 if-else と自己参照による再帰が用いられる。
ここでは「自己参照縛り」があるということでその通りにはいかないものの、次のようにある程度原型を留めた形で記述できる。
fac = (\n -> (foldr (.) id . replicate (n+1) $ \f i -> if (i > 0) then i * f(i-1) else 1) id n)やっていることは単純で、不動点コンビネータに渡した時に得られる不動点が階乗関数となるような関数を \(f\) としたとき、入力 \(n\) に対して、
- base-case にたどり着けるのに十分な回数分 (\(n+1\) 回) \(f\) を合成した関数 \(f^{n+1}\) を作り、その関数に恒等射を適用して得られる関数に \(n\) を入力して得られる出力
を出力している
Point-free な定義たち
無限リストを用いた定義
まずは Haskell の遅延評価によって実現する無限リストを活用した例。
fac = (product . (flip take $ [1..]))コードについて説明を加えると、まず flip という関数に take という関数を渡すことによって「リストの入力 xs に対して、『整数の入力 i に対して、xs の i 番目の値までを抽出した新たなリストを作る関数』を構成する関数 flip take」を得る。続いて、その関数に「1以上の整数全体のリスト [1..]」を入力することで、「整数の入力 i に対して、[1..] の i 番目の値までを抽出した新たなリストを作る関数」簡単に言い換えると、「整数の入力 i に対して、リスト [1..i] を作る関数」が得られる。そしてあとはこの関数に先ほどの例1にも登場した product を合成してあげることで、「整数の入力 i に対して、値 product [1..i] を求める関数」が作れてしまうという流れである。
flip という関数に take という関数を渡すことによって「リストの入力 xs に対して、『整数の入力 i に対して、xs の i 番目の値までを抽出した新たなリストを作る関数』を構成する関数 flip take」を得る。続いて、その関数に「1以上の整数全体のリスト [1..]」を入力することで、「整数の入力 i に対して、[1..] の i 番目の値までを抽出した新たなリストを作る関数」簡単に言い換えると、「整数の入力 i に対して、リスト [1..i] を作る関数」が得られる。そしてあとはこの関数に先ほどの例1にも登場した product を合成してあげることで、「整数の入力 i に対して、値 product [1..i] を求める関数」が作れてしまうという流れである。英語版 Wikipedia に掲載されていた定義
英語版 Wikipedia の Point-free スタイルでの実装例の一つ として紹介されているもの。
fac = ((foldr (*) 1) . (enumFromTo 1))基本的に一つ前の例とやっていることは一緒である。
というのも、enumFromTo 1 は「整数の入力 i に対して、リスト [1..i] を作る関数」であり、foldr (*) 1 も product と (純粋関数としての) 違いがない。
というのも、
enumFromTo 1 は「整数の入力 i に対して、リスト [1..i] を作る関数」であり、foldr (*) 1 も product と (純粋関数としての) 違いがない。ETCS 集合論での階乗の役割を果たす射の構成法をもとにした定義
圏論的な集合論である ETCS 集合論における階乗関数の構成法 になぞって実装を行ったもの。
fac = ((!!) ((fmap snd) (iterate (((<*>).fmap (,)) (succ.fst) (uncurry (*).((<*>).fmap (,)) (succ.fst) snd))$(0,1))))掛け算 (*) をより根源的な関数である succ を使って構成した関数で書き換えると
(*) をより根源的な関数である succ を使って構成した関数で書き換えるとfac = ((!!) ((fmap snd) (iterate (((<*>).fmap (,)) (succ.fst) (uncurry((!!) (iterate (curry(uncurry((!!) (iterate (curry(succ.uncurry id)) id)).(((<*>).fmap (,)) (uncurry id) snd))) (const 0))).((<*>).fmap (,)) (succ.fst) snd))$(0,succ 0))))※後者のコードはビルトインの足し算や掛け算を使用していないため実行速度はかなり遅くなることに注意。僕の Haskell 開発環境では、後者の方法で階乗を定義した場合、「10の階乗 10!」が限界。(そもそもの Int 型の上限値の問題もあるけど) 一方、例1の方法であれば「100000の階乗 100000!」もサクサクと計算可能。
Int 型の上限値の問題もあるけど) 一方、例1の方法であれば「100000の階乗 100000!」もサクサクと計算可能。これまでの例はなんとなく実際に動作することをイメージできてしまうかもしれないが、この例に関してはそれらと比べるとイメージしづらいことと思う。
ということで是非自身で実際にコードが動作することを確認してみてほしい。
ということで是非自身で実際にコードが動作することを確認してみてほしい。
もし手元にHaskellの開発環境が無く、さらにコンパイラをインストールするのが面倒という場合であれば、Haskell 公式サイト のトップページにオンラインインタプリタのようなものが用意されているのでそれを活用するというのもよいかもしれない。
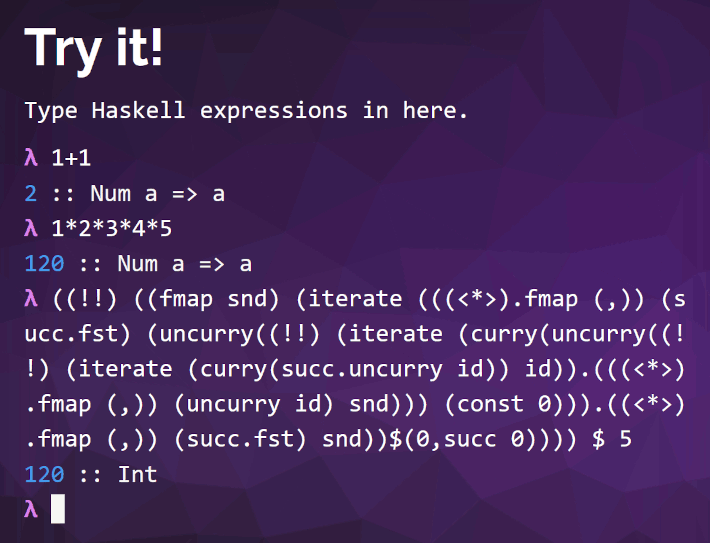
具体的には「Try it!」という部分に、
((!!) ((fmap snd) (iterate (((<*>).fmap (,)) (succ.fst) (uncurry((!!) (iterate (curry(uncurry((!!) (iterate (curry(succ.uncurry id)) id)).(((<*>).fmap (,)) (uncurry id) snd))) (const 0))).((<*>).fmap (,)) (succ.fst) snd))$(0,succ 0)))) $ 5を入力し実行することで、以下のように実際に「5の階乗」である「120」がちゃんと表示されることを確認することができる。
「通常の自己参照を含んだ定義を与えられた縛りの中で無理やり真似てみたもの」の Point-free バージョン
Point-free ではない階乗関数の実装の１つとして紹介した「通常の自己参照を含んだ定義を与えられた縛りの中で無理やり真似てみたもの」は圏論的な考え方を使って Point-free の形に書き換えることができる。
実際にやってみると、以下が得られる。
fac = ((uncurry id).(uncurry $ (<*>).fmap(,))((((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(curry(snd), (curry(((uncurry id).(uncurry $ (<*>).fmap(,))(((uncurry either)(curry(fst.snd),curry(snd.snd)).(((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(Right, Left.(uncurry either)(id, id))).fst, id.snd)).(uncurry $ (<*>).fmap(,))((((uncurry id).(uncurry $ (<*>).fmap(,))((((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(curry(snd), curry(fst.(((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))((uncurry $ (<*>).fmap(,))(const(0),const(0)), (uncurry $ (<*>).fmap(,))(snd, succ.snd)).(uncurry id))).fst, id.snd).(uncurry $ (<*>).fmap(,))(snd, fst)).(uncurry $ (<*>).fmap(,))((const(1)).(const()),id).((uncurry id).(uncurry $ (<*>).fmap(,))((((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(curry(snd), curry(fst.(((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))((uncurry $ (<*>).fmap(,))(const(0),const(0)), (uncurry $ (<*>).fmap(,))(snd, succ.snd)).(uncurry id))).fst, id.snd).(uncurry $ (<*>).fmap(,))(snd, fst))).(uncurry $ (<*>).fmap(,))((const(1)).(const()),snd),(uncurry $ (<*>).fmap(,))(( (uncurry id).(uncurry $ (<*>).fmap(,))((((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(curry((const(0).(const())).snd), curry(((uncurry id).(uncurry $ (<*>).fmap(,))((((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))(curry(snd), curry(succ.(uncurry id))).fst, id.snd)).(uncurry $ (<*>).fmap(,))((uncurry id),snd) )).fst, id.snd)).(uncurry $ (<*>).fmap(,))(snd, (uncurry id).(uncurry $ (<*>).fmap(,))(id.fst, fst.(((!!).(uncurry.flip $ iterate)).(uncurry $ (<*>).fmap(,))((flip($) ()).fst, id.snd))((uncurry $ (<*>).fmap(,))(const(0),const(0)), (uncurry $ (<*>).fmap(,))(snd, succ.snd)).snd)) , (const(1)).(const())))))).succ,id))１つ前に紹介したものについては、公式サイト上の Haskell インタプリタでも動作したのだが、こちらは長くて込み入り過ぎているのか「Unable to get type and value of expression: ...」といった感じに上手く処理されない。
とはいえ、見ての通り「Prelude 標準モジュール内の関数」以外は一切使っていないことからわかるように、たとえばローカルにインストールした Haskell インタプリタとかをちゃんと使えばしっかり動作する。
例として、「5 の階乗」を実行した結果のスクリーンショットを以下に貼り付けておく。
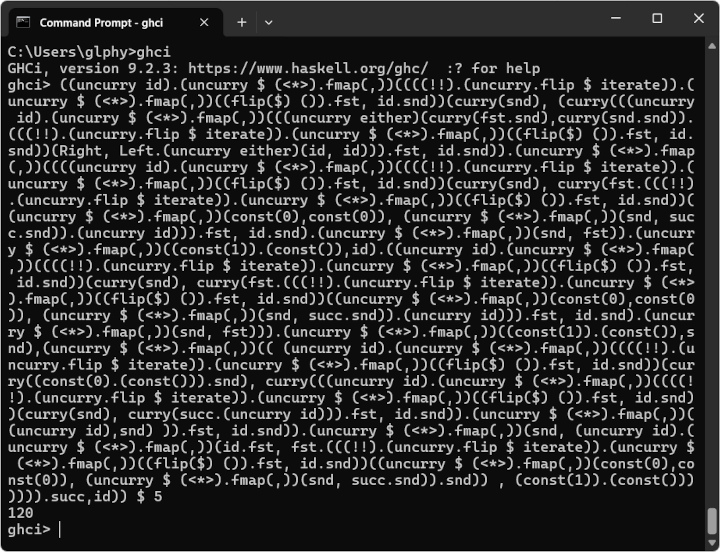
ここまでくると、流石に圏論を多少なりともかじっている人でない限り何がどうなっているのかまでを即座に理解することは難しいかもしれないが、ここではひとまず「圏論はちゃんと使いこなせば、ほんと何でもできてしまう」ということを垣間見ていただければ幸いである。
ここでコードが異様に長くなっている理由については
- IF 分岐そのもの
- 小なり (<)::Int->Int->Bool (IF分岐の判定部で必要になるもの)
- 整数同士の引き算 (-)::Int->Int->Int (厳密には自然数同士の引き算)
- 整数同士の掛け算 (*)::Int->Int->Int
などなどをブラックボックス化された中身のわからない漠然とした記号ではなく、具体的で詳細な構成が与えられた形として直接書き下している点に着目すればわかるだろう。
ちなみに圏論徒向けの余談だが、ここでの IF分岐に対してであれば、わざわざ余積の考えを持ち出すことなく構成すること自体は可能であるとはいえ、例えばこのコードを継続渡しスタイルに書き換えるとなったとき、結局余積を使った分岐の構築が必要になるので、敢えて余積を回避しない汎用性の高い形で記述している。
タグ一覧: