QR コードの仕様を学ぶ - 誤り訂正コード語の算出

大雑把な概観の説明
PureScript による具体的な実装を行うことで、大雑把な概観から解像度を少し上げ、ビット演算として計算していた事との繋がりを理解する
最後に圏論的集合論の基礎に則ったかなり詳細な写像の構成を行うことで、数学的な曖昧さの解消に努める (ここは数学的厳密さが気になってしまう人向けなので、気にならない人は読まなくて大丈夫です)

という3つの流れで紹介していくことにする。

概観

まずは、対象や射の詳細かつ具体的な構成は置いておきつつ、大雑把な話の流れをつかみやすくするための構成の概観を紹介する。

環 \({\mathbb{Z}}\) (記号の濫用だが、この概観の節ではご勘弁を)、その環の持つ整数 2 が生成する \({\mathbb{Z}}\) の主イデアル \(2{\mathbb{Z}}\) に対して、その商環 \({\mathbb{Z}} / 2{\mathbb{Z}}\) は体をなす。

ここで、その体 \({\mathbb{Z}} / 2{\mathbb{Z}}\) 上の多項式環 \({\mathbb{Z}} / 2{\mathbb{Z}}[X]\) について、\(\xi\) を、ざっと次の条件を満たすその環の (基底集合の) 要素 (i.e. \({\mathbb{Z}} / 2{\mathbb{Z}}\) を係数に持つ多項式) とする。

【条件】

まず、\(\xi\) が生成する \({\mathbb{Z}} / 2{\mathbb{Z}}[X]\) の主イデアルによる商として得られる商環 \(R\) が体をなし、その上で

\(0_R\) を \(R\) の加法単位元
\(\pi\) を \({\mathbb{Z}} / 2{\mathbb{Z}}[X]\) から商環 \(R\) への商写像
\(\delta_1\) を一次の項だけからなり、かつその一次の不定元の係数が \({\mathbb{Z}} / 2{\mathbb{Z}}\) の乗法単位元となっている \({\mathbb{Z}} / 2{\mathbb{Z}}\) 係数の多項式
\({\rm assign}\) を \({\mathbb{Z}} / 2{\mathbb{Z}}\) 係数の多項式 \(\eta\) の不定元に \(R\) の値 \(\alpha\) を代入して得られる \(R\) の値を与える写像

としたとき、 \(R\) の任意の値 \(x\) が \(\pi(\delta_1)\) 同士の有限回の積を通して行きつくことができて、さらに

\[ {\rm assign}(\eta, \pi(\delta_1)) = 0_R \]

を満たす最大次数が最小かつ、その最大次数を持つ不定元の係数が \({\mathbb{Z}} / 2{\mathbb{Z}}\) の乗法単位元 \(1_{{\mathbb{Z}} / 2{\mathbb{Z}}}\) であるような非自明な多項式 \(\eta\) が \(\xi\) それ自体である。

余談

多項式 \(\xi\) の生成する主イデアルによる商として体が得られるとなれば、その多項式 \(\xi\) が \(\pi(\delta_1)\) を根として持つことは自明であり、あとはそれが次数最小の非自明なモニック多項式であり、かつ \(R\) の原始元となっていればここでの必要な要件が満たされることになるため、わかりやすさを重視し上の形で条件を与えている。

しかし本来原始元は一般に一意ではないので、厳密さを重視した場合、より一般的抽象的な記述になる点に注意してほしい。

...っといった感じの条件になるが、概観を知る現段階ではこの条件の意味があまりパッとしなくても悩まずに、なんとなく「それが生成する主イデアルで多項式環 \({\mathbb{Z}} / 2{\mathbb{Z}}[X]\) を割ってあげると、色々と都合のいい条件を持つ数の体系が出来上がるような特殊な多項式」程度の認識で大丈夫だと思う。

さて話を本筋に戻すが、以下の \({\mathbb{Z}} / 2{\mathbb{Z}}\) 係数の多項式

\[ 1X^8 + 0X^7 + 0X^6 + 0X^5 + 1X^4 + 1X^3 + 1X^2 + 0X + 1 \]

は、先の条件を満たす多項式であり、そこで多項式環 \({\mathbb{Z}} / 2{\mathbb{Z}}[X]\) をその多項式の生成する主イデアルで割って得られる体を \({\rm GF}(256)\) とすることにしよう。(実際にその条件を満たす事実確認については、PureScript を使った総当たりを次節で行うので、こちらも今は特に悩む必要はない)

ここで、

\({\rm fromCodeWord}\) をコード語に対応する整数のリスト \({\rm ns}\) を、\({\rm ns}\) の要素として含まれている整数を商写像 \(\pi\) を介して \({\rm GF}(256)\) の要素に変換したうえで、それら \({\rm GF}(256)\) の要素を係数に対応させた \({\rm GF}(256)\) 係数の多項式を与える写像
\(g_n\) をこれから生成したい QRコードのエラー訂正コード語数 \(n\) に対応する特定の \({\rm GF}(256)\) 係数の多項式
\({\rm mod}_{{\rm GF}(256)}\) を \({\rm GF}(256)\) 係数の多項式同士の剰余を与える写像
\({\rm toCodeWord}\) を \({\rm GF}(256)\) 係数の多項式から、コード語に対応する整数のリストを与える写像

とする。

この時、誤り訂正コード語に対応する整数のリスト \({\rm ns'}\) は、コード語に対応する整数のリスト \({\rm ns}\) を使って

\[ {\rm ns'} = {\rm toCodeWord}({\rm mod}_{{\rm GF}(256)}({\rm fromCodeWord}({\rm ns}),g_n)) \]

という感じで計算されるというのが、誤り訂正コード語のざっくりとした計算方法となる。

ちなみにもう少しだけ具体的にいうと \(g_n\) は、

\(\delta_{1;256}\) を一次の項だけからなり、かつその一次の不定元の係数が \({\rm GF}(256)\) の乗法単位元となっている \({\rm GF}(256)\) 係数の多項式

としたとき、

\[ g_n = \prod_{k=0}^{n-1} (\delta_{1;256} - (\pi(\delta_1))^k) \]

として定まるものである。

PureScript での実装

数の体系を組み立てる

ℤ/2ℤ の組み立て

(..)

data GF2 = Zero_GF2 | One_GF2

instance Show GF2 where
  show a =
    case a of
      Zero_GF2 -> "0_GF2"
      One_GF2  -> "1_GF2"

instance Eq GF2 where
  eq a b =
    case (Tuple a b) of
      -- 0 == 0 = True
      (Tuple Zero_GF2 Zero_GF2) -> true
      -- 0 == 1 = False
      (Tuple Zero_GF2 One_GF2)  -> false
      -- 1 == 0 = False
      (Tuple One_GF2 Zero_GF2)  -> false
      -- 1 == 1 = True
      (Tuple One_GF2 One_GF2)   -> true


instance Semiring GF2 where
  add a b =
    case (Tuple a b) of
      -- 0 + 0 = 0
      (Tuple Zero_GF2 Zero_GF2) -> Zero_GF2
      -- 0 + 1 = 1
      (Tuple Zero_GF2 One_GF2)  -> One_GF2
      -- 1 + 0 = 1
      (Tuple One_GF2 Zero_GF2)  -> One_GF2
      -- 1 + 1 = 0
      (Tuple One_GF2 One_GF2)   -> Zero_GF2
  zero = Zero_GF2

  mul a b =
    case (Tuple a b) of
      -- 0 * 0 = 0
      (Tuple Zero_GF2 Zero_GF2) -> Zero_GF2
      -- 0 * 1 = 0
      (Tuple Zero_GF2 One_GF2)  -> Zero_GF2
      -- 1 * 0 = 0
      (Tuple One_GF2 Zero_GF2)  -> Zero_GF2
      -- 1 * 1 = 1
      (Tuple One_GF2 One_GF2)   -> One_GF2
  one = One_GF2

addInv_GF2 c =
  case c of
    Zero_GF2 -> Zero_GF2
    One_GF2  -> One_GF2

mulInv_GF2 c =
  case c of
    Zero_GF2 -> Zero_GF2 -- ダミー
    One_GF2  -> One_GF2

instance Ring GF2 where
  sub a b = add a (addInv_GF2 b)

instance CommutativeRing GF2

instance EuclideanRing GF2 where
  degree = const one
  div a b = mul a (mulInv_GF2 b)
  mod = const zero

instance DivisionRing GF2 where
  recip = mulInv_GF2

ℤ/2ℤ 係数の多項式環の組み立て

(..)

zipForPolynomial :: forall a b. Semiring a => Semiring b => Array a -> Array b -> Array (Tuple a b)
zipForPolynomial xs ys = zip xs' ys'
  where
    xs' = (replicate (max (length xs) (length ys) - length xs) zero) <> xs
    ys' = (replicate (max (length xs) (length ys) - length ys) zero) <> ys

data PolynomialOverGF2 = PolynomialOverGF2(Array GF2)

delta_1 = PolynomialOverGF2([One_GF2,Zero_GF2])

instance Show PolynomialOverGF2 where
  show (PolynomialOverGF2 xs) = show xs

instance Eq PolynomialOverGF2 where
  eq (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) =
    (dropWhile (_ == zero) xs == dropWhile (_ == zero) ys)


instance Semiring PolynomialOverGF2 where
  -- 多項式同士の和
  add (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) = PolynomialOverGF2 $ dropWhile (_ == zero) do
    (Tuple x y) <- zipForPolynomial xs ys
    pure $ add x y
  zero = PolynomialOverGF2([])
  -- 多項式同士の積
  mul (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) = foldr add zero $ do
      (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
      pure $ PolynomialOverGF2 $ do
        y <- (ys <> replicate n zero)
        pure $ mul x y
  one = PolynomialOverGF2(pure $ One_GF2)

addInv_PolynomialOverGF2 (PolynomialOverGF2 xs) = PolynomialOverGF2 $ do
  x <- xs
  pure $ addInv_GF2 x

instance Ring PolynomialOverGF2 where
  sub a b = add a (addInv_PolynomialOverGF2 b)

instance CommutativeRing PolynomialOverGF2

isZero_GF2 :: PolynomialOverGF2 -> Boolean
isZero_GF2 (PolynomialOverGF2 xs) = (xs == [])

getDegree_PGF2 :: PolynomialOverGF2 -> Int
getDegree_PGF2 (PolynomialOverGF2 xs) = max 0 (length (dropWhile (_ == zero) xs) - 1)
getCoeff_PGF2 :: PolynomialOverGF2 -> GF2
getCoeff_PGF2 (PolynomialOverGF2 xs) =
  case (xs !! 0) of
    Just fstElm -> fstElm
    Nothing     -> zero
genPolynomial_PGF2 :: Int -> GF2 -> PolynomialOverGF2
genPolynomial_PGF2 deg coe = PolynomialOverGF2 $ (pure coe) <> replicate deg zero

div_mod_PGF2 :: (Tuple PolynomialOverGF2 PolynomialOverGF2) -> Tuple PolynomialOverGF2 PolynomialOverGF2
div_mod_PGF2 (Tuple d1 d2) =
  (#) (Tuple zero d1) $ foldr ($) (const zero) $
    replicate (getDegree_PGF2 d1 + 1) $ \rec (Tuple res_div res_mod) ->
      let
        xs_deg = getDegree_PGF2 res_mod
        ys_deg = getDegree_PGF2 d2
        a      = getCoeff_PGF2 res_mod
        b      = getCoeff_PGF2 d2
        del    = xs_deg - ys_deg
      in
        if (del >= 0) && not(isZero_GF2(res_mod)) then
          let
            res_div' = res_div  + genPolynomial_PGF2 del (a*recip(b))
            res_mod' = res_mod - (genPolynomial_PGF2 del (a*recip(b)))*d2
          in
            rec(Tuple res_div' res_mod')
        else
          Tuple res_div res_mod

instance EuclideanRing PolynomialOverGF2 where
  degree = getDegree_PGF2
  div = curry(fst <<< div_mod_PGF2)
  mod = curry(snd <<< div_mod_PGF2)

GF(256) の組み立て

(..)

data GF256 = GF256(PolynomialOverGF2)
prim = PolynomialOverGF2 [One_GF2,Zero_GF2,Zero_GF2,Zero_GF2,One_GF2,One_GF2,One_GF2,Zero_GF2,One_GF2]

quot :: PolynomialOverGF2 -> GF256
quot = GF256

isOne_GF256 :: GF256 -> Boolean
isOne_GF256 (GF256 x) =
  case (x `mod` prim) of
    (PolynomialOverGF2 zs) -> (zs == [One_GF2])      

instance Show GF256 where
  show (GF256 x) = show x

instance Eq GF256 where
  eq (GF256 x) (GF256 y) =
    (x `mod` prim) == (y `mod` prim)

instance Semiring GF256 where
  add (GF256 x) (GF256 y) = GF256 $
    (x + y) `mod` prim
  zero = (GF256 zero)
  mul (GF256 x) (GF256 y) = GF256 $
    (x * y) `mod` prim
  one = (GF256 one)

addInv_GF256 (GF256 x) = 
  GF256 $ addInv_PolynomialOverGF2 x

mulInv_GF256 x@(GF256 dat) =
  if isZero_GF2(dat) then
    zero
  else
    let
      ys = do
        d7 <- [Zero_GF2,One_GF2]
        d6 <- [Zero_GF2,One_GF2]
        d5 <- [Zero_GF2,One_GF2]
        d4 <- [Zero_GF2,One_GF2]
        d3 <- [Zero_GF2,One_GF2]
        d2 <- [Zero_GF2,One_GF2]
        d1 <- [Zero_GF2,One_GF2]
        d0 <- [Zero_GF2,One_GF2]
        pure $ GF256(PolynomialOverGF2(dropWhile (_ == zero) [d7,d6,d5,d4,d3,d2,d1,d0]))
      tbl = do
        y <- ys
        if isOne_GF256(x*y) then
          pure y
        else
          []
    in
      if length(tbl) == 1 then
        case tbl !! 0 of
          Just res -> res
          Nothing  -> zero
      else
        zero

instance Ring GF256 where
  sub a b = add a (addInv_GF256 b)

instance CommutativeRing GF256

instance EuclideanRing GF256 where
  degree = const one
  div a b = mul a (mulInv_GF256 b)
  mod = const zero

instance DivisionRing GF256 where
  recip = mulInv_GF256

fieldExt_GF2_GF256 :: GF2 -> GF256
fieldExt_GF2_GF256 x =
  quot(PolynomialOverGF2 [x])

GF(256) 係数の多項式環の組み立て

(..)

data PolynomialOverGF256 = PolynomialOverGF256(Array GF256)

delta_1_256 = PolynomialOverGF256([one,zero])

instance Show PolynomialOverGF256 where
  show (PolynomialOverGF256 xs) = show xs

instance Eq PolynomialOverGF256 where
  eq (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) =
    (dropWhile (_ == zero) xs == dropWhile (_ == zero) ys)

instance Semiring PolynomialOverGF256 where
  add (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) = PolynomialOverGF256 $ dropWhile (_ == zero) do
    (Tuple x y) <- zipForPolynomial xs ys
    pure $ add x y
  zero = PolynomialOverGF256([])
  mul (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) = foldr add zero $ do
      (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
      pure $ PolynomialOverGF256 $ do
        y <- (ys <> replicate n zero)
        pure $ mul x y
  one = PolynomialOverGF256([one])

addInv_PolynomialOverGF256 (PolynomialOverGF256 xs) = PolynomialOverGF256 $ do
  x <- xs
  pure $ addInv_GF256 x

instance Ring PolynomialOverGF256 where
  sub a b = add a (addInv_PolynomialOverGF256 b)

instance CommutativeRing PolynomialOverGF256

isZero_GF256 :: PolynomialOverGF256 -> Boolean
isZero_GF256 (PolynomialOverGF256 xs) = (xs == [])

getDegree_PGF256 :: PolynomialOverGF256 -> Int
getDegree_PGF256 (PolynomialOverGF256 xs) = max 0 (length (dropWhile (_ == zero) xs) - 1)
getCoeff_PGF256 :: PolynomialOverGF256 -> GF256
getCoeff_PGF256 (PolynomialOverGF256 xs) =
  case (xs !! 0) of
    Just fstElm -> fstElm
    Nothing     -> zero
genPolynomial_PGF256 :: Int -> GF256 -> PolynomialOverGF256
genPolynomial_PGF256 deg coe = PolynomialOverGF256 $ (pure coe) <> replicate deg zero

div_mod_PGF256 :: (Tuple PolynomialOverGF256 PolynomialOverGF256) -> Tuple PolynomialOverGF256 PolynomialOverGF256
div_mod_PGF256 (Tuple d1 d2) =
  (#) (Tuple zero d1) $ foldr ($) (const zero) $
    replicate (getDegree_PGF256 d1 + 1) $ \rec (Tuple res_div res_mod) ->
      let
        xs_deg = getDegree_PGF256 res_mod
        ys_deg = getDegree_PGF256 d2
        a      = getCoeff_PGF256 res_mod
        b      = getCoeff_PGF256 d2
        del    = xs_deg - ys_deg
      in
        if (del >= 0) && not(isZero_GF256(res_mod)) then
          let
            res_div' = res_div  + genPolynomial_PGF256 del (a*recip(b))
            res_mod' = res_mod - (genPolynomial_PGF256 del (a*recip(b)))*d2
          in
            rec(Tuple res_div' res_mod')
        else
          Tuple res_div res_mod

instance EuclideanRing PolynomialOverGF256 where
  degree = getDegree_PGF256
  div = curry(fst <<< div_mod_PGF256)
  mod = curry(snd <<< div_mod_PGF256)

伏線回収

さてピースは一通りそろったので、伏線回収をしていこう。

GF(256) の原始元の確認

理論的には、GF(256) は原始元を 128 個持つのだが、これについて総当たりで確認することができる。

GF(256) の要素 \(x\) が原始元であるのかは、「\(x\) が原始的な 1 の 255 乗根であること (\(x\) を 255 乗すると 1 になる且つ 255 乗するまでに一度も 1 にならないこと)」から判別され、その判別関数は PureScript を使えば以下のように組み立てることができる。

isPrimitiveElm_GF256 :: GF256 -> Boolean
isPrimitiveElm_GF256 x =
  (#) (Tuple 1 one) $ foldr ($) (const false) $
    replicate 255 $ \rec (Tuple i current) ->
      if current*x == one then
        i == 255
      else
        rec $ Tuple (i+1) (current*x)

これがあれば、以下の

main :: Effect Unit
main = do
  let
    ys = do
      d7 <- [Zero_GF2,One_GF2]
      d6 <- [Zero_GF2,One_GF2]
      d5 <- [Zero_GF2,One_GF2]
      d4 <- [Zero_GF2,One_GF2]
      d3 <- [Zero_GF2,One_GF2]
      d2 <- [Zero_GF2,One_GF2]
      d1 <- [Zero_GF2,One_GF2]
      d0 <- [Zero_GF2,One_GF2]
      pure $ GF256(PolynomialOverGF2(dropWhile (_ == zero) [d7,d6,d5,d4,d3,d2,d1,d0]))
    output = foldr (<>) "" $ do
      y <- ys
      pure $ (show $ isPrimitiveElm_GF256(y)) <> "\t" <> show(y) <> "\n"

  log $ output

を使って、GF(256) のどの要素が原始元であるのかを一覧で確認することができる。

全てを表示すると見づらいので、最初の幾つかだけを例としてここに載せておく。(全部見たい場合は、自身でこの PureScript コードを実行して確かめてほしい。)

false   []
false   [1_GF2]
true    [1_GF2,0_GF2]
false   [1_GF2,1_GF2]
true    [1_GF2,0_GF2,0_GF2]
false   [1_GF2,0_GF2,1_GF2]
true    [1_GF2,1_GF2,0_GF2]
false   [1_GF2,1_GF2,1_GF2]
false   [1_GF2,0_GF2,0_GF2,0_GF2]
true    [1_GF2,0_GF2,0_GF2,1_GF2]
false   [1_GF2,0_GF2,1_GF2,0_GF2]
false   [1_GF2,0_GF2,1_GF2,1_GF2]
false   [1_GF2,1_GF2,0_GF2,0_GF2]
true    [1_GF2,1_GF2,0_GF2,1_GF2]
true    [1_GF2,1_GF2,1_GF2,0_GF2]
false   [1_GF2,1_GF2,1_GF2,1_GF2]
true    [1_GF2,0_GF2,0_GF2,0_GF2,0_GF2]
false   [1_GF2,0_GF2,0_GF2,0_GF2,1_GF2]
true    [1_GF2,0_GF2,0_GF2,1_GF2,0_GF2]
true    [1_GF2,0_GF2,0_GF2,1_GF2,1_GF2]
true    [1_GF2,0_GF2,1_GF2,0_GF2,0_GF2]

true

となっているもの、つまり上の一覧の中に示されているものでいえば

\[ \begin{align} &\pi(\delta_1) \\ &(\pi(\delta_1))^2 \\ &(\pi(\delta_1))^2 + \pi(\delta_1) \\ &(\pi(\delta_1))^3 + 1 \\ &(\pi(\delta_1))^3 + (\pi(\delta_1))^2 + 1 \\ &(\pi(\delta_1))^3 + (\pi(\delta_1))^2 + \pi(\delta_1) \\ &(\pi(\delta_1))^4 \\ &(\pi(\delta_1))^4 + \pi(\delta_1) \\ &(\pi(\delta_1))^4 + \pi(\delta_1) + 1 \\ &(\pi(\delta_1))^4 + (\pi(\delta_1))^2 \\ \end{align} \]

が全て原始元であり、実際 \(\pi(\delta_1)\) が GF(256) の原始元であることの確認がこれでできたわけである。

該当の多項式が例の条件を満たすことを確認する (最小多項式であったことの確認)

まず例の代入を行う写像は、PureScript では次のように組み立てることができる。

assign :: PolynomialOverGF2 -> GF256 -> GF256
assign (PolynomialOverGF2 xs) a = foldr (+) zero $ do
  (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
  pure $ (fieldExt_GF2_GF256 x) * (foldr (*) one $ replicate n a)

つまり差し当たり

main :: Effect Unit
main = do
  let
    xs = do
      d8 <- [Zero_GF2,One_GF2]
      d7 <- [Zero_GF2,One_GF2]
      d6 <- [Zero_GF2,One_GF2]
      d5 <- [Zero_GF2,One_GF2]
      d4 <- [Zero_GF2,One_GF2]
      d3 <- [Zero_GF2,One_GF2]
      d2 <- [Zero_GF2,One_GF2]
      d1 <- [Zero_GF2,One_GF2]
      d0 <- [Zero_GF2,One_GF2]
      pure $ PolynomialOverGF2(dropWhile (_ == zero) [d8,d7,d6,d5,d4,d3,d2,d1,d0])
    output = foldr (<>) "" $ do
      eta <- xs
      pure $ show eta <> "\t" <> (show $ (assign eta (quot delta_1)) == zero) <> "\n"

  log $ output

で、最大次数が 8 以下の全ての \({\mathbb{Z}} / 2{\mathbb{Z}}\) 係数の多項式に対して、例の条件が満たされるかどうかを総当たりで確認することができる。

非自明なもの除いた一番最初に

true

を与えている多項式をその出力の中から探してみると... (流石に出力を全部載せるとページが見づらくなるのでその周辺だけをピックアップした)

[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,0_GF2,1_GF2,0_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,0_GF2,1_GF2,0_GF2,1_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,0_GF2,1_GF2,1_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,0_GF2,1_GF2,1_GF2,1_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,0_GF2,0_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,0_GF2,0_GF2,1_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,0_GF2,1_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,0_GF2,1_GF2,1_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,1_GF2,0_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,1_GF2,0_GF2,1_GF2] true
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,1_GF2,1_GF2,0_GF2] false
[1_GF2,0_GF2,0_GF2,0_GF2,1_GF2,1_GF2,1_GF2,1_GF2,1_GF2] false
[1_GF2,0_GF2,0_GF2,1_GF2,0_GF2,0_GF2,0_GF2,0_GF2,0_GF2] false

確かに \({\rm GF}(256)\) を構成するのに使った多項式のそれになっていることがわかっただろう。

余談

こういった良い性質を持つ多項式が、俗にいう (体論の文脈での) 「原始多項式 (primitive polynomial)」と呼ばれるものなのだが、ぱっと見だと天下り的でわかりにくいと思う。

多項式 gₙ の具体的な展開された形を確認する

せっかくなので、多項式 \(g_n\) の計算を行う関数も作ってみよう。

とはいっても先に述べたように計算式は

\[ g_n = \prod_{k=0}^{n-1} (\delta_{1;256} - (\pi(\delta_1))^k) \]

と、至ってシンプルなものであり PureScript で次のようにそのまま書き下すことができる。

g :: Int -> PolynomialOverGF256
g n = foldr (*) one $ do
  k <- 0..(n-1)
  pure $ delta_1_256 - PolynomialOverGF256[foldr (*) one $ replicate k (quot(delta_1))]

一応はこれで多項式 \(g_n\) の計算自体はできるのだが、多項式の内容が把握しづらいのは少し不便ではあるので、その辺の問題を緩和できるように、

\[ (\pi(\delta_1))^{k_n} \cdot X^n + (\pi(\delta_1))^{k_{n-1}} \cdot X^{n-1} + \cdots + (\pi(\delta_1))^{k_1} \cdot X^1 + (\pi(\delta_1))^{k_0} \cdot X^0 \]

の形で文字列化するような関数

myShow

も一緒に作っておく。(関数名がテキトーなのは気にしないように！)

stringToListOfChars :: String -> Array Char
stringToListOfChars str =
  arr2
  where
    arr1 = toCodePointArray str
    arr2 = do
      x_maybe <- (map $ toEnum <<< fromEnum) arr1
      case x_maybe of
        Just c  -> pure c
        Nothing -> pure ' '

listOfCharsToString :: Array Char -> String
listOfCharsToString listOfChars = foldr (<>) "" $
  (map $ singleton <<< codePointFromChar) listOfChars

read :: Char -> Int
read c =
  case c of
    '0' -> 0
    '1' -> 1
    '2' -> 2
    '3' -> 3
    '4' -> 4
    '5' -> 5
    '6' -> 6
    '7' -> 7
    '8' -> 8
    '9' -> 9
    _   -> 0


power :: Int -> Int -> Int
power a b =
  foldr (*) 1 (replicate b a)

tinyText =
  ["⁰","¹","²","³","⁴","⁵","⁶","⁷","⁸","⁹"]


myShow :: PolynomialOverGF256 -> String
myShow (PolynomialOverGF256 xs) = drop 3 $ foldr (<>) "" $ do
  (Tuple m (GF256 (PolynomialOverGF2 ys))) <- zip (reverse $ 0..(length xs - 1)) xs
  let
    tmp = foldr (+) 0 $ do
      (Tuple n y) <- zip (reverse $ 0..(length ys - 1)) ys
      case y of
        Zero_GF2 -> pure $ 0
        One_GF2  -> pure $ shl 1 n
    tmp2 = foldr (<>) "" $ do
      c1 <- stringToListOfChars $ show(m)
      case tinyText!!(read(c1)) of
        Just c2 -> pure $ c2
        Nothing -> []
    tmp3 = foldr (<>) "" $ do
      c1 <- stringToListOfChars $ (show $ toExp_1(tmp))
      case tinyText!!(read(c1)) of
        Just c2 -> pure $ c2
        Nothing -> []
  pure $ " + (π(δ₁))" <> tmp3 <> "･X" <> tmp2

これを使って、\(n\) に 2 から 20 までの整数を適用した結果の一覧を、次の

main :: Effect Unit
main = do
  let
    output3 = foldr (<>) "" $ do
      n <- (2..20)
      pure $ (myShow $ g(n)) <> "\n"

  log $ output3

を実行して取得してみると...

(π(δ₁))⁰･X² + (π(δ₁))²⁵･X¹ + (π(δ₁))¹･X⁰
(π(δ₁))⁰･X³ + (π(δ₁))¹⁹⁸･X² + (π(δ₁))¹⁹⁹･X¹ + (π(δ₁))³･X⁰
(π(δ₁))⁰･X⁴ + (π(δ₁))⁷⁵･X³ + (π(δ₁))²⁴⁹･X² + (π(δ₁))⁷⁸･X¹ + (π(δ₁))⁶･X⁰
(π(δ₁))⁰･X⁵ + (π(δ₁))¹¹³･X⁴ + (π(δ₁))¹⁶⁴･X³ + (π(δ₁))¹⁶⁶･X² + (π(δ₁))¹¹⁹･X¹ + (π(δ₁))¹⁰･X⁰
(π(δ₁))⁰･X⁶ + (π(δ₁))¹⁶⁶･X⁵ + (π(δ₁))⁰･X⁴ + (π(δ₁))¹³⁴･X³ + (π(δ₁))⁵･X² + (π(δ₁))¹⁷⁶･X¹ + (π(δ₁))¹⁵･X⁰
(π(δ₁))⁰･X⁷ + (π(δ₁))⁸⁷･X⁶ + (π(δ₁))²²⁹･X⁵ + (π(δ₁))¹⁴⁶･X⁴ + (π(δ₁))¹⁴⁹･X³ + (π(δ₁))²³⁸･X² + (π(δ₁))¹⁰²･X¹ + (π(δ₁))²¹･X⁰
(π(δ₁))⁰･X⁸ + (π(δ₁))¹⁷⁵･X⁷ + (π(δ₁))²³⁸･X⁶ + (π(δ₁))²⁰⁸･X⁵ + (π(δ₁))²⁴⁹･X⁴ + (π(δ₁))²¹⁵･X³ + (π(δ₁))²⁵²･X² + (π(δ₁))¹⁹⁶･X¹ + (π(δ₁))²⁸･X⁰
(π(δ₁))⁰･X⁹ + (π(δ₁))⁹⁵･X⁸ + (π(δ₁))²⁴⁶･X⁷ + (π(δ₁))¹³⁷･X⁶ + (π(δ₁))²³¹･X⁵ + (π(δ₁))²³⁵･X⁴ + (π(δ₁))¹⁴⁹･X³ + (π(δ₁))¹¹･X² + (π(δ₁))¹²³･X¹ + (π(δ₁))³⁶･X⁰
(π(δ₁))⁰･X¹⁰ + (π(δ₁))²⁵¹･X⁹ + (π(δ₁))⁶⁷･X⁸ + (π(δ₁))⁴⁶･X⁷ + (π(δ₁))⁶¹･X⁶ + (π(δ₁))¹¹⁸･X⁵ + (π(δ₁))⁷⁰･X⁴ + (π(δ₁))⁶⁴･X³ + (π(δ₁))⁹⁴･X² + (π(δ₁))³²･X¹ + (π(δ₁))⁴⁵･X⁰
(π(δ₁))⁰･X¹¹ + (π(δ₁))²²⁰･X¹⁰ + (π(δ₁))¹⁹²･X⁹ + (π(δ₁))⁹¹･X⁸ + (π(δ₁))¹⁹⁴･X⁷ + (π(δ₁))¹⁷²･X⁶ + (π(δ₁))¹⁷⁷･X⁵ + (π(δ₁))²⁰⁹･X⁴ + (π(δ₁))¹¹⁶･X³ + (π(δ₁))²²⁷･X² + (π(δ₁))¹⁰･X¹ + (π(δ₁))⁵⁵･X⁰
(π(δ₁))⁰･X¹² + (π(δ₁))¹⁰²･X¹¹ + (π(δ₁))⁴³･X¹⁰ + (π(δ₁))⁹⁸･X⁹ + (π(δ₁))¹²¹･X⁸ + (π(δ₁))¹⁸⁷･X⁷ + (π(δ₁))¹¹³･X⁶ + (π(δ₁))¹⁹⁸･X⁵ + (π(δ₁))¹⁴³･X⁴ + (π(δ₁))¹³¹･X³ + (π(δ₁))⁸⁷･X² + (π(δ₁))¹⁵⁷･X¹ + (π(δ₁))⁶⁶･X⁰
(π(δ₁))⁰･X¹³ + (π(δ₁))⁷⁴･X¹² + (π(δ₁))¹⁵²･X¹¹ + (π(δ₁))¹⁷⁶･X¹⁰ + (π(δ₁))¹⁰⁰･X⁹ + (π(δ₁))⁸⁶･X⁸ + (π(δ₁))¹⁰⁰･X⁷ + (π(δ₁))¹⁰⁶･X⁶ + (π(δ₁))¹⁰⁴･X⁵ + (π(δ₁))¹³⁰･X⁴ + (π(δ₁))²¹⁸･X³ + (π(δ₁))²⁰⁶･X² + (π(δ₁))¹⁴⁰･X¹ + (π(δ₁))⁷⁸･X⁰
(π(δ₁))⁰･X¹⁴ + (π(δ₁))¹⁹⁹･X¹³ + (π(δ₁))²⁴⁹･X¹² + (π(δ₁))¹⁵⁵･X¹¹ + (π(δ₁))⁴⁸･X¹⁰ + (π(δ₁))¹⁹⁰･X⁹ + (π(δ₁))¹²⁴･X⁸ + (π(δ₁))²¹⁸･X⁷ + (π(δ₁))¹³⁷･X⁶ + (π(δ₁))²¹⁶･X⁵ + (π(δ₁))⁸⁷･X⁴ + (π(δ₁))²⁰⁷･X³ + (π(δ₁))⁵⁹･X² + (π(δ₁))²²･X¹ + (π(δ₁))⁹¹･X⁰
(π(δ₁))⁰･X¹⁵ + (π(δ₁))⁸･X¹⁴ + (π(δ₁))¹⁸³･X¹³ + (π(δ₁))⁶¹･X¹² + (π(δ₁))⁹¹･X¹¹ + (π(δ₁))²⁰²･X¹⁰ + (π(δ₁))³⁷･X⁹ + (π(δ₁))⁵¹･X⁸ + (π(δ₁))⁵⁸･X⁷ + (π(δ₁))⁵⁸･X⁶ + (π(δ₁))²³⁷･X⁵ + (π(δ₁))¹⁴⁰･X⁴ + (π(δ₁))¹²⁴･X³ + (π(δ₁))⁵･X² + (π(δ₁))⁹⁹･X¹ + (π(δ₁))¹⁰⁵･X⁰
(π(δ₁))⁰･X¹⁶ + (π(δ₁))¹²⁰･X¹⁵ + (π(δ₁))¹⁰⁴･X¹⁴ + (π(δ₁))¹⁰⁷･X¹³ + (π(δ₁))¹⁰⁹･X¹² + (π(δ₁))¹⁰²･X¹¹ + (π(δ₁))¹⁶¹･X¹⁰ + (π(δ₁))⁷⁶･X⁹ + (π(δ₁))³･X⁸ + (π(δ₁))⁹¹･X⁷ + (π(δ₁))¹⁹¹･X⁶ + (π(δ₁))¹⁴⁷･X⁵ + (π(δ₁))¹⁶⁹･X⁴ + (π(δ₁))¹⁸²･X³ + (π(δ₁))¹⁹⁴･X² + (π(δ₁))²²⁵･X¹ + (π(δ₁))¹²⁰･X⁰
(π(δ₁))⁰･X¹⁷ + (π(δ₁))⁴³･X¹⁶ + (π(δ₁))¹³⁹･X¹⁵ + (π(δ₁))²⁰⁶･X¹⁴ + (π(δ₁))⁷⁸･X¹³ + (π(δ₁))⁴³･X¹² + (π(δ₁))²³⁹･X¹¹ + (π(δ₁))¹²³･X¹⁰ + (π(δ₁))²⁰⁶･X⁹ + (π(δ₁))²¹⁴･X⁸ + (π(δ₁))¹⁴⁷･X⁷ + (π(δ₁))²⁴･X⁶ + (π(δ₁))⁹⁹･X⁵ + (π(δ₁))¹⁵⁰･X⁴ + (π(δ₁))³⁹･X³ + (π(δ₁))²⁴³･X² + (π(δ₁))¹⁶³･X¹ + (π(δ₁))¹³⁶･X⁰
(π(δ₁))⁰･X¹⁸ + (π(δ₁))²¹⁵･X¹⁷ + (π(δ₁))²³⁴･X¹⁶ + (π(δ₁))¹⁵⁸･X¹⁵ + (π(δ₁))⁹⁴･X¹⁴ + (π(δ₁))¹⁸⁴･X¹³ + (π(δ₁))⁹⁷･X¹² + (π(δ₁))¹¹⁸･X¹¹ + (π(δ₁))¹⁷⁰･X¹⁰ + (π(δ₁))⁷⁹･X⁹ + (π(δ₁))¹⁸⁷･X⁸ + (π(δ₁))¹⁵²･X⁷ + (π(δ₁))¹⁴⁸･X⁶ + (π(δ₁))²⁵²･X⁵ + (π(δ₁))¹⁷⁹･X⁴ + (π(δ₁))⁵･X³ + (π(δ₁))⁹⁸･X² + (π(δ₁))⁹⁶･X¹ + (π(δ₁))¹⁵³･X⁰
(π(δ₁))⁰･X¹⁹ + (π(δ₁))⁶⁷･X¹⁸ + (π(δ₁))³･X¹⁷ + (π(δ₁))¹⁰⁵･X¹⁶ + (π(δ₁))¹⁵³･X¹⁵ + (π(δ₁))⁵²･X¹⁴ + (π(δ₁))⁹⁰･X¹³ + (π(δ₁))⁸³･X¹² + (π(δ₁))¹⁷･X¹¹ + (π(δ₁))¹⁵⁰･X¹⁰ + (π(δ₁))¹⁵⁹･X⁹ + (π(δ₁))⁴⁴･X⁸ + (π(δ₁))¹²⁸･X⁷ + (π(δ₁))¹⁵³･X⁶ + (π(δ₁))¹³³･X⁵ + (π(δ₁))²⁵²･X⁴ + (π(δ₁))²²²･X³ + (π(δ₁))¹³⁸･X² + (π(δ₁))²²⁰･X¹ + (π(δ₁))¹⁷¹･X⁰
(π(δ₁))⁰･X²⁰ + (π(δ₁))¹⁷･X¹⁹ + (π(δ₁))⁶⁰･X¹⁸ + (π(δ₁))⁷⁹･X¹⁷ + (π(δ₁))⁵⁰･X¹⁶ + (π(δ₁))⁶¹･X¹⁵ + (π(δ₁))¹⁶³･X¹⁴ + (π(δ₁))²⁶･X¹³ + (π(δ₁))¹⁸⁷･X¹² + (π(δ₁))²⁰²･X¹¹ + (π(δ₁))¹⁸⁰･X¹⁰ + (π(δ₁))²²¹･X⁹ + (π(δ₁))²²⁵･X⁸ + (π(δ₁))⁸³･X⁷ + (π(δ₁))²³⁹･X⁶ + (π(δ₁))¹⁵⁶･X⁵ + (π(δ₁))¹⁶⁴･X⁴ + (π(δ₁))²¹²･X³ + (π(δ₁))²¹²･X² + (π(δ₁))¹⁸⁸･X¹ + (π(δ₁))¹⁹⁰･X⁰

JIS 規格の \(g\) の一覧表と照らし合わせてみればわかるが、ちゃんと正しい計算が出来ていることの確認がとれるだろう。

余談

もしかすると、例の \(g\) の一覧表を初めて目にした際、そのごちゃごちゃ加減に圧倒された人が少なからずいるとは思うが、このように導出自体は別にそこまで複雑なものではなかったりするのである。

(..)

通常のもっとシンプルなビット演算や対応表を使ったコードとの関係性

実用向けの GF(256) の積

既に数学理論ベースでの GF(256) の積は構成できているので、一応それを使って誤り訂正コード語の計算を行う準備は整っている。

一方で実用性を考える場合、パフォーマンスの問題もあり、残念ながらその定義に愚直に則ってコーティングを行った関数をそのまま使用することはあまりおすすめされない。

そしてその問題を解消する際にポイントとなってくるのが、原始元の存在である。

というのも GF(256) の任意の原始元を \(\alpha\) とし、さらに

\({\rm toExp}_{\alpha}\) を GF(256) の要素 \(x\) に対して、その要素の指数表記 \(\alpha^n\) の肩に乗っている \(n\) を与える写像
\({\rm fromExp}_{\alpha}\) を自然数 \(n\) に対して、GF(256) の要素 \(\alpha^n\) を与える写像

とすると、それらを使って GF(256) における積を、以下のように単なる「自然数の和」として処理させることが可能となる。

\[ \begin{align} x\cdot y &= \alpha^{{\rm toExp}_{\alpha}(x)}\cdot\alpha^{{\rm toExp}_{\alpha}(y)} \\ &= \alpha^{{\rm toExp}_{\alpha}(x) + {\rm toExp}_{\alpha}(y)} \\ &= {\rm fromExp}_{\alpha}({\rm toExp}_{\alpha}(x) + {\rm toExp}_{\alpha}(y)) \\ \end{align} \]

ここで重要なのは、\({\rm toExp}_{\alpha}\) と \({\rm fromExp}_{\alpha}\) のそれぞれの関数は、事前に計算しておいた有限長のデータテーブルの参照という形で記述させることによって、出力を得るまでの過程の中から煩雑な「多項式の掛け算の計算処理」を省くことが可能なところにあり、それによって大きなパフォーマンス向上が見込めるのである。

余談

極論を行ってしまえば GF(256) は有限体なので、順序対 \(\langle x,y \rangle\) と積 \(x\cdot y\) を対応させるための有限長のデータテーブルすら同様に作っておくこともできるのだが、それはそれで今度はメモリの問題が生じてくることになる。

例1: 原始元 α に π(δ₁) を選んだ場合

まずは、JIS 規格も含め、通常行われている原始元の選び方となる、

\[ \alpha = π(δ₁) \]

の場合のデータテーブルを作ってみる。

fromExp_1 :: Int -> Int
fromExp_1 n =
  case prodTbl1_fromExp!!(n `mod` 255) of
    Just x  -> x
    Nothing -> 0
toExp_1 :: Int -> Int
toExp_1 x =
  case prodTbl1_toExp!!x of
    Just n  -> n
    Nothing -> 0
prodTbl1_fromExp =
  [1,2,4,8,16,32,64,128,29,58,116,232,205,135,19,38
  ,76,152,45,90,180,117,234,201,143,3,6,12,24,48,96,192
  ,157,39,78,156,37,74,148,53,106,212,181,119,238,193,159,35
  ,70,140,5,10,20,40,80,160,93,186,105,210,185,111,222,161
  ,95,190,97,194,153,47,94,188,101,202,137,15,30,60,120,240
  ,253,231,211,187,107,214,177,127,254,225,223,163,91,182,113,226
  ,217,175,67,134,17,34,68,136,13,26,52,104,208,189,103,206
  ,129,31,62,124,248,237,199,147,59,118,236,197,151,51,102,204
  ,133,23,46,92,184,109,218,169,79,158,33,66,132,21,42,84
  ,168,77,154,41,82,164,85,170,73,146,57,114,228,213,183,115
  ,230,209,191,99,198,145,63,126,252,229,215,179,123,246,241,255
  ,227,219,171,75,150,49,98,196,149,55,110,220,165,87,174,65
  ,130,25,50,100,200,141,7,14,28,56,112,224,221,167,83,166
  ,81,162,89,178,121,242,249,239,195,155,43,86,172,69,138,9
  ,18,36,72,144,61,122,244,245,247,243,251,235,203,139,11,22
  ,44,88,176,125,250,233,207,131,27,54,108,216,173,71,142,1]
prodTbl1_toExp =
  [0,0,1,25,2,50,26,198,3,223,51,238,27,104,199,75
  ,4,100,224,14,52,141,239,129,28,193,105,248,200,8,76,113
  ,5,138,101,47,225,36,15,33,53,147,142,218,240,18,130,69
  ,29,181,194,125,106,39,249,185,201,154,9,120,77,228,114,166
  ,6,191,139,98,102,221,48,253,226,152,37,179,16,145,34,136
  ,54,208,148,206,143,150,219,189,241,210,19,92,131,56,70,64
  ,30,66,182,163,195,72,126,110,107,58,40,84,250,133,186,61
  ,202,94,155,159,10,21,121,43,78,212,229,172,115,243,167,87
  ,7,112,192,247,140,128,99,13,103,74,222,237,49,197,254,24
  ,227,165,153,119,38,184,180,124,17,68,146,217,35,32,137,46
  ,55,63,209,91,149,188,207,205,144,135,151,178,220,252,190,97
  ,242,86,211,171,20,42,93,158,132,60,57,83,71,109,65,162
  ,31,45,67,216,183,123,164,118,196,23,73,236,127,12,111,246
  ,108,161,59,82,41,157,85,170,251,96,134,177,187,204,62,90
  ,203,89,95,176,156,169,160,81,11,245,22,235,122,117,44,215
  ,79,174,213,233,230,231,173,232,116,214,244,234,168,80,88,175]

例2: 原始元 α に (π(δ₁))³ + (π(δ₁))² + 1 を選んだ場合

先ほど、一般に選択されがちな原始元を採用した場合のデータテーブルを作ってみたが、別にどの原始元を採用して作ったデータテーブルを用いるのかは、最終的な GF(256) の積の計算結果には一切影響を与えない。(使用するテーブルが全く異なっていようが同じ結果を与える。)

その事実を確認する意味も含めて、2つ目の例では一般には選ばれない原始元 \((\pi(\delta_1))^3 + (\pi(\delta_1))^2 + \pi(\delta_1)\) を使ったデータテーブルの作成を行う。

fromExp_2 :: Int -> Int
fromExp_2 n =
  case prodTbl2_fromExp!!(n `mod` 255) of
    Just x  -> x
    Nothing -> 0
toExp_2 :: Int -> Int
toExp_2 x =
  case prodTbl2_toExp!!x of
    Just n  -> n
    Nothing -> 0
prodTbl2_fromExp =
  [1,13,81,186,209,116,62,43,194,179,180,151,61,60,49,96
  ,218,11,127,65,106,168,27,175,56,5,57,8,104,178,185,198
  ,135,237,69,94,241,201,204,245,253,149,39,158,88,223,50,119
  ,41,216,17,221,40,213,64,103,249,161,126,76,59,18,202,219
  ,6,46,251,187,220,37,132,250,182,141,159,85,142,136,166,93
  ,230,58,31,155,97,215,90,197,144,30,150,48,109,139,177,174
  ,53,84,131,217,28,140,146,4,52,89,210,99,205,248,172,47
  ,246,234,102,244,240,196,157,79,44,225,25,181,154,108,134,224
  ,20,228,32,189,242,222,63,38,147,9,101,227,3,23,243,211
  ,110,156,66,125,91,200,193,164,71,68,83,160,115,29,129,195
  ,190,229,45,236,72,15,75,24,184,203,214,87,148,42,207,226
  ,14,70,73,2,26,162,105,191,232,124,86,153,123,117,51,122
  ,120,98,192,169,22,254,130,212,77,54,67,112,10,114,16,208
  ,121,111,145,19,199,138,188,255,143,133,247,231,55,78,33,176
  ,163,100,238,82,173,34,167,80,183,128,206,239,95,252,152,118
  ,36,137,171,12,92,235,107,165,74,21,233,113,7,35,170,1]
prodTbl2_toExp =
  [0,0,179,140,103,25,64,252,27,137,204,17,243,1,176,165
  ,206,50,61,211,128,249,196,141,167,122,180,22,100,157,89,82
  ,130,222,229,253,240,69,135,42,52,48,173,7,120,162,65,111
  ,91,14,46,190,104,96,201,220,24,26,81,60,13,12,6,134
  ,54,19,146,202,153,34,177,152,164,178,248,166,59,200,221,119
  ,231,2,227,154,97,75,186,171,44,105,86,148,244,79,35,236
  ,15,84,193,107,225,138,114,55,28,182,20,246,125,92,144,209
  ,203,251,205,156,5,189,239,47,192,208,191,188,185,147,58,18
  ,233,158,198,98,70,217,126,32,77,241,213,93,101,73,76,216
  ,88,210,102,136,172,41,90,11,238,187,124,83,145,118,43,74
  ,155,57,181,224,151,247,78,230,21,195,254,242,110,228,95,23
  ,223,94,29,9,10,123,72,232,168,30,3,67,214,131,160,183
  ,194,150,8,159,117,87,31,212,149,37,62,169,38,108,234,174
  ,207,4,106,143,199,53,170,85,49,99,16,63,68,51,133,45
  ,127,121,175,139,129,161,80,219,184,250,113,245,163,33,226,235
  ,116,36,132,142,115,39,112,218,109,56,71,66,237,40,197,215]

数学的な曖昧さの除去

最後に僕にとって一番重要 (であり、多くの人にとっては世界一どうでもいい点) となる「諸々の写像が、 ETCS 集合論の基礎の上で構成可能な実体あるものであるという事実」を示していく。

可換環 K を係数に持つ多項式全体の集合の構成

まず数学的厳密に考えた場合、例えば「有理数全体の集合」というものが「分数の形の記号全体の集合」として構成できなかった点を思い出してほしい。

純粋数学的な手段による意味付けのされていない漠然とした記号「\(\frac{a}{b}\)」そのものを直接「集める」ということ自体が意味をなさないため、わざわざタプル \(\langle a,b \rangle\) を出発点に、それらタプルの間の相等関係が意図する形になる適切な同値関係による商をとって得られる対象の要素として「分数」に相当する概念を得ていたわけである。

多項式についても同様に、

\[ a_n\cdot X^n + a_{n-1}\cdot X^{n-1} + \cdots + a_1\cdot X^1 + a_0\cdot X^0 \]

という形の「記号全体の集合」として「可換環 \(K\) を係数に持つ多項式全体の集合」を直接構成することはできなくて、しっかりと公理として認めている正規の手続きを経て構成していかなければならない。

集合構成の与え方に絶対的なものはないが、ここでは ETCS 集合論と親和性が高そうな構成を実践していく。

余談

理想としては、この「多項式全体からなる集合」も普遍性の観点から直接的に取り扱いたいのだが、残念ながらこれについては「自由対象」と呼ばれる集合の圏のだけ中で簡単に話が完結しない普遍的構成が必要になってくる。

現在の「公理化された集合の圏の上で数学を行う ETCS」では、積対象や引き戻しなどと同様の公理的な普遍性の取り扱いを自由対象に対しても行うことは難しいため、ここでは「多項式全体からなる集合」はゴリゴリと構成させていただくことにする。

まず、ETCS 集合論的に、可換環 \(K\) とは、

対象 \(X_K:X_K\rightarrow X_K\) [\(K\) の基底集合 (underlying set)]
射 \((+_K):X_K\times X_K\rightarrow X_K\) [\(K\) の加法]
射 \((0_K):1\rightarrow X_K\) [\(K\) の加法単位元]
射 \({\rm addInv}:X_K\rightarrow X_K\) [\(K\) の任意の値に対する加法逆元を誘導する写像]
射 \((\cdot_K):X_K\times X_K\rightarrow X_K\) [\(K\) の乗法]
射 \((1_K):1\rightarrow X_K\) [\(K\) の乗法単位元]

という射一式の内、特定の条件を満足するものとして扱われることを念頭に置いておいてほしい。(その詳しい条件については、わざわざここで説明する内容ではないため省略。)

一応どうしてこんなことを明示したのかというと、「現時点で手元にある既知の射が、具体的に何であるのかを事前にはっきりさせておきたい」という意図があったためである。

というのも、ETCS ではない通常の集合論の文脈で「可換環 \(K\)」といった場合、\(K\) という記号はその可換環の基底集合を指し示す記号として解釈されがちで、それによりどうしても「その構造に付随していなければならない基底集合以外の構成要素の存在たち」を見失いがちであるためである。(ちなみに、概観の節で「環 \({\mathbb{Z}}\)」を記号の濫用と注意書きしているのもその理由による。)

では話を戻すが、そもそもその

\[ a_n\cdot X^n + a_{n-1}\cdot X^{n-1} + \cdots + a_1\cdot X^1 + a_0\cdot X^0 \]

という記号から抽出できなければならない情報が何であるのかを抽象的に考えてみよう。

それは「\(n+1\) 個の可換環 \(K\) の基底集合 \(X_K\) の要素」であり、それは「\(X_K\) の要素の有限族」としてフォーマルに与えることができることに気付く。(多項式としてあるべき加法と乗法の構造は後から構成するので、その点についてはまだ考えなくてよい。)

とはいえ「\(X_K\) の要素の有限族 \(I\rightarrow X_K\)」というのは、添え字集合 \(I\) が異なると "型" が変わってしまうため、「それら全体の集合」をそのままの意味で考えようとすると行き詰まってしまう。

現在の設定の上では、2対象 \(A,B\) 間の任意の矢印を要素に持つ1つの対象の構成は指数対象 \(B^A\) という形で可能なので、その点に着目して少しだけ工夫することで「\(X_K\) の要素の有限族全体からなる対象」の構成ができる。

これについても絶対的な１つの方法があるわけではないが、この記事では以下の形で構成する。

「\({\mathbb{N}}\) を添え字集合とする \(X_K\) の要素の族 \(\xi\) と自然数 \(n\) の順序対 \(\langle \xi, n \rangle\)」からなる対象に相当する指数対象との積対象 \({(X_K)}^{\mathbb{N}} \times {\mathbb{N}}\) に対し、「\(\langle \xi, n \rangle\) の内、\(n\) より大きい任意の自然数 \(m\) に対して、\(\xi_m\) が \(K\) の加法単位元 \(0_K\) でありかつ、\(n\) が \(0_{\mathbb{N}}\) より大きい場合、\(\xi_n\) が \(K\) における加法単位元 \(0_K\) でない」という条件を満足するものを抽出して得られる \({(X_K)}^{\mathbb{N}} \times {\mathbb{N}}\) の部分対象

あまり数学的な厳密さを重視しない文献などでは、その部分集合は

\[ \{ \langle \xi, n \rangle \in {(X_K)}^{\mathbb{N}} \times {\mathbb{N}} \:|\: \forall m\in{\mathbb{N}}[(m > n) \Rightarrow \xi_m = 0_K] \wedge ((n > 0_{\mathbb{N}}) \Rightarrow \xi_n \ne 0_K) \} \]

で "定義" されるように説明されるかもしれないが、ETCS だと、上の記号列を提示しても、その部分集合が実際に "構成" されたことを意味しないので、厳密な定義としては不十分である。

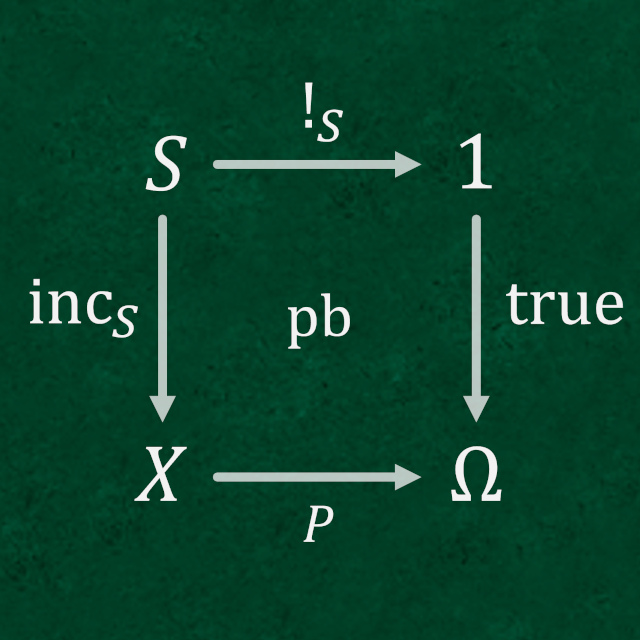
では具体的に何をすればいいのかというと、その「\({(X_K)}^{\mathbb{N}} \times {\mathbb{N}}\) の要素を抽出する条件式」が、真理値対象をコドメインにとる１つの射 \(P:{(X_K)}^{\mathbb{N}} \times {\mathbb{N}}\rightarrow \Omega\) として構成できることを示せばよい。

ETCS 公理系を満たす任意の圏で、諸々の論理演算子が一般に構成できることは、以下の

置換公理型を認めない初等トポスの一般論の中で、集合 {x∈X|P(x)} はどのようにして構成されるのかtakulabo.sakura.ne.jp

で説明した通りなので、それら射を使って先の条件式の構成を考えていく。

\[ \begin{align} P(\xi, n) &= \forall m:{\mathbb{N}}[(m > n) \Rightarrow \xi_m = 0_K] \wedge ((n > 0_{\mathbb{N}}) \Rightarrow \xi_n \ne 0_K) \\ P(\langle \xi, n\rangle) &= \forall m:{\mathbb{N}}[(n <_{\mathbb{N}} m) \Rightarrow \xi(m) = 0_K] \wedge ((0_{\mathbb{N}} <_{\mathbb{N}} n) \Rightarrow \xi(n) \ne 0_K) \\ \langle \xi, n\rangle {\sf \, ⨟ \,} P &= \forall m:{\mathbb{N}}[(n <_{\mathbb{N}} m) \Rightarrow (\langle \xi, m \rangle {\sf \, ⨟ \,} {\rm ev} = 0_K)] \wedge ((0_{\mathbb{N}} <_{\mathbb{N}} n) \Rightarrow (\langle \xi, n \rangle {\sf \, ⨟ \,} {\rm ev} \ne 0_K)) \\ &= \forall m:{\mathbb{N}}[(\langle n,m\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}})) \Rightarrow (\langle \langle \xi, m \rangle {\sf \, ⨟ \,} {\rm ev} , 0_K\rangle {\sf \, ⨟ \,} (==))] \wedge ((\langle 0_{\mathbb{N}}, n\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}})) \Rightarrow (\langle \langle \xi, n \rangle {\sf \, ⨟ \,} {\rm ev}, 0_K\rangle {\sf \, ⨟ \,} (\ne) )) \\ &= \forall m:{\mathbb{N}}[\langle \langle n,m\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle \xi, m \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] \wedge (\langle \langle 0_{\mathbb{N}}, n\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle \langle \xi, n \rangle {\sf \, ⨟ \,} {\rm ev}, 0_K\rangle {\sf \, ⨟ \,} ((==) {\sf \, ⨟ \,} (\neg))\rangle {\sf \, ⨟ \,} (\Rightarrow)) \\ &= \forall m:{\mathbb{N}}[\langle \langle \xi, n\rangle ,m\rangle {\sf \, ⨟ \,} \langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] \wedge (\langle \langle 0_{\mathbb{N}}, n\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle \langle \xi, n \rangle {\sf \, ⨟ \,} {\rm ev}, 0_K\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow)) \\ &= (\langle \xi, n\rangle {\sf \, ⨟ \,} \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}})) \wedge (\langle \langle 0_{\mathbb{N}}, n\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle \langle \xi, n \rangle {\sf \, ⨟ \,} {\rm ev}, 0_K\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow)) \\ &= (\langle \xi, n\rangle {\sf \, ⨟ \,} \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}})) \wedge (\langle \xi, n\rangle {\sf \, ⨟ \,} \langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle \xi, n\rangle {\sf \, ⨟ \,} \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow)) \\ &= (\langle \xi, n\rangle {\sf \, ⨟ \,} \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}})) \wedge (\langle \xi, n\rangle {\sf \, ⨟ \,} (\langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow))) \\ &= \langle \langle \xi, n\rangle {\sf \, ⨟ \,} \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}}), \langle \xi, n\rangle {\sf \, ⨟ \,} (\langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow))\rangle {\sf \, ⨟ \,} (\wedge) \\ \langle \xi, n\rangle {\sf \, ⨟ \,} P &= \langle \xi, n\rangle {\sf \, ⨟ \,} (\langle \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}}), (\langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow))\rangle {\sf \, ⨟ \,} (\wedge)) \\ \end{align} \]

つまり、

\[ P = \langle \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}}), (\langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow))\rangle {\sf \, ⨟ \,} (\wedge) \]

で構成できる。

この射が構成できれば、欲しい部分対象は \(\langle K[X], P^{-1}({\rm true}) \rangle\) として得られる。

ではここから、集合 \(K[X]\) 上に可換環の構造を組み立てていくのだが、まず多項式の次数 (degree) を求める射 \({\rm getDegree}:K[X]\rightarrow {\mathbb{N}}\) から構成しよう。

勘の良い人なら気付いたかもしれないが、多項式全体の集合の構成を行う際、単に「族全体」ではなく「族と自然数の順序対全体」として親の集合を与えていたのは、この射の構成を見越した上でのことだったのである。

実際、その構成を採用していることによって、\({\rm getDegree}:K[X]\rightarrow {\mathbb{N}}\) は単に

\[ \begin{align} {\rm getDegree} &= P^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_2 \\ &= (\langle \lambda[\langle \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_2, {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm prj}_1 {\sf \, ⨟ \,} {\rm prj}_1, {\rm prj}_2 \rangle {\sf \, ⨟ \,} \langle {\rm ev} , {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==)\rangle {\sf \, ⨟ \,} (\Rightarrow)] {\sf \, ⨟ \,} (\forall_{\mathbb{N}}), (\langle \langle {\rm const}(0_{\mathbb{N}}), {\rm prj}_2\rangle {\sf \, ⨟ \,} (<_{\mathbb{N}}), \langle {\rm ev}, {\rm const}(0_K)\rangle {\sf \, ⨟ \,} (==) {\sf \, ⨟ \,} (\neg)\rangle {\sf \, ⨟ \,} (\Rightarrow))\rangle {\sf \, ⨟ \,} (\wedge))^{-1}({\rm true}) {\sf \, ⨟ \,} {\rm prj}_2 \\ \end{align} \]

で構成することができる。

δ₁ を形あるものとして構成しよう！

本編では、

という説明の後に、\(\delta_1\) という記号を持ち込んでいるが、その詳しい構成方法についてはそこでは触れなかった。

その「未構成の形ない空っぽの記号」が使われていることに不満がある人はもちろんいると思うので、その ETCS 集合論的な構成についてもここで考えていく。

まずそれは体 \(GF(2)\) 上の多項式なので、先ほど一般的に定義した集合の具体的な1つである集合 \(GF(2)[X]\) の要素 \(\delta_1:1\rightarrow GF(2)[X]\) となる。

このページで使用したコード

数の体系の組み立て

module Main where

import Prelude
import Effect (Effect)
import Effect.Console (log)
import Data.Int.Bits (shl)
import Data.Array
import Data.Maybe
import Data.Tuple
import Data.String (drop)
import Data.String.CodePoints (codePointFromChar, toCodePointArray, singleton)
import Data.Enum

main :: Effect Unit
main = do
  let
    xs = do
      d8 <- [Zero_GF2,One_GF2]
      d7 <- [Zero_GF2,One_GF2]
      d6 <- [Zero_GF2,One_GF2]
      d5 <- [Zero_GF2,One_GF2]
      d4 <- [Zero_GF2,One_GF2]
      d3 <- [Zero_GF2,One_GF2]
      d2 <- [Zero_GF2,One_GF2]
      d1 <- [Zero_GF2,One_GF2]
      d0 <- [Zero_GF2,One_GF2]
      pure $ PolynomialOverGF2(dropWhile (_ == zero) [d8,d7,d6,d5,d4,d3,d2,d1,d0])
    output = foldr (<>) "" $ do
      eta <- xs
      pure $ show eta <> "\t" <> (show $ (assign eta (quot delta_1)) == zero) <> "\n"

  log $ output


g :: Int -> PolynomialOverGF256
g n = foldr (*) one $ do
  k <- 0..(n-1)
  pure $ delta_1_256 - PolynomialOverGF256[foldr (*) one $ replicate k (quot(delta_1))]



stringToListOfChars :: String -> Array Char
stringToListOfChars str =
  arr2
  where
    arr1 = toCodePointArray str
    arr2 = do
      x_maybe <- (map $ toEnum <<< fromEnum) arr1
      case x_maybe of
        Just c  -> pure c
        Nothing -> pure ' '

listOfCharsToString :: Array Char -> String
listOfCharsToString listOfChars = foldr (<>) "" $
  (map $ singleton <<< codePointFromChar) listOfChars

read :: Char -> Int
read c =
  case c of
    '0' -> 0
    '1' -> 1
    '2' -> 2
    '3' -> 3
    '4' -> 4
    '5' -> 5
    '6' -> 6
    '7' -> 7
    '8' -> 8
    '9' -> 9
    _   -> 0


power :: Int -> Int -> Int
power a b =
  foldr (*) 1 (replicate b a)

tinyText =
  ["⁰","¹","²","³","⁴","⁵","⁶","⁷","⁸","⁹"]


myShow :: PolynomialOverGF256 -> String
myShow (PolynomialOverGF256 xs) = drop 3 $ foldr (<>) "" $ do
  (Tuple m (GF256 (PolynomialOverGF2 ys))) <- zip (reverse $ 0..(length xs - 1)) xs
  let
    tmp = foldr (+) 0 $ do
      (Tuple n y) <- zip (reverse $ 0..(length ys - 1)) ys
      case y of
        Zero_GF2 -> pure $ 0
        One_GF2  -> pure $ shl 1 n
    tmp2 = foldr (<>) "" $ do
      c1 <- stringToListOfChars $ show(m)
      case tinyText!!(read(c1)) of
        Just c2 -> pure $ c2
        Nothing -> []
    tmp3 = foldr (<>) "" $ do
      c1 <- stringToListOfChars $ (show $ toExp_1(tmp))
      case tinyText!!(read(c1)) of
        Just c2 -> pure $ c2
        Nothing -> []
  pure $ " + (π(δ₁))" <> tmp3 <> "･X" <> tmp2



primElm1 = GF256 $ PolynomialOverGF2 [One_GF2,Zero_GF2]
primElm2 = GF256 $ PolynomialOverGF2 [One_GF2,One_GF2,Zero_GF2,One_GF2]

fromExp_1 :: Int -> Int
fromExp_1 n =
  case prodTbl1_fromExp!!(n `mod` 255) of
    Just x  -> x
    Nothing -> 0
toExp_1 :: Int -> Int
toExp_1 x =
  case prodTbl1_toExp!!x of
    Just n  -> n
    Nothing -> 0
prodTbl1_fromExp =
    [1,2,4,8,16,32,64,128,29,58,116,232,205,135,19,38
    ,76,152,45,90,180,117,234,201,143,3,6,12,24,48,96,192
    ,157,39,78,156,37,74,148,53,106,212,181,119,238,193,159,35
    ,70,140,5,10,20,40,80,160,93,186,105,210,185,111,222,161
    ,95,190,97,194,153,47,94,188,101,202,137,15,30,60,120,240
    ,253,231,211,187,107,214,177,127,254,225,223,163,91,182,113,226
    ,217,175,67,134,17,34,68,136,13,26,52,104,208,189,103,206
    ,129,31,62,124,248,237,199,147,59,118,236,197,151,51,102,204
    ,133,23,46,92,184,109,218,169,79,158,33,66,132,21,42,84
    ,168,77,154,41,82,164,85,170,73,146,57,114,228,213,183,115
    ,230,209,191,99,198,145,63,126,252,229,215,179,123,246,241,255
    ,227,219,171,75,150,49,98,196,149,55,110,220,165,87,174,65
    ,130,25,50,100,200,141,7,14,28,56,112,224,221,167,83,166
    ,81,162,89,178,121,242,249,239,195,155,43,86,172,69,138,9
    ,18,36,72,144,61,122,244,245,247,243,251,235,203,139,11,22
    ,44,88,176,125,250,233,207,131,27,54,108,216,173,71,142,1]
prodTbl1_toExp =
    [0,0,1,25,2,50,26,198,3,223,51,238,27,104,199,75
    ,4,100,224,14,52,141,239,129,28,193,105,248,200,8,76,113
    ,5,138,101,47,225,36,15,33,53,147,142,218,240,18,130,69
    ,29,181,194,125,106,39,249,185,201,154,9,120,77,228,114,166
    ,6,191,139,98,102,221,48,253,226,152,37,179,16,145,34,136
    ,54,208,148,206,143,150,219,189,241,210,19,92,131,56,70,64
    ,30,66,182,163,195,72,126,110,107,58,40,84,250,133,186,61
    ,202,94,155,159,10,21,121,43,78,212,229,172,115,243,167,87
    ,7,112,192,247,140,128,99,13,103,74,222,237,49,197,254,24
    ,227,165,153,119,38,184,180,124,17,68,146,217,35,32,137,46
    ,55,63,209,91,149,188,207,205,144,135,151,178,220,252,190,97
    ,242,86,211,171,20,42,93,158,132,60,57,83,71,109,65,162
    ,31,45,67,216,183,123,164,118,196,23,73,236,127,12,111,246
    ,108,161,59,82,41,157,85,170,251,96,134,177,187,204,62,90
    ,203,89,95,176,156,169,160,81,11,245,22,235,122,117,44,215
    ,79,174,213,233,230,231,173,232,116,214,244,234,168,80,88,175]

fromExp_2 :: Int -> Int
fromExp_2 n =
  case prodTbl2_fromExp!!(n `mod` 255) of
    Just x  -> x
    Nothing -> 0
toExp_2 :: Int -> Int
toExp_2 x =
  case prodTbl2_toExp!!x of
    Just n  -> n
    Nothing -> 0
prodTbl2_fromExp =
    [1,13,81,186,209,116,62,43,194,179,180,151,61,60,49,96
    ,218,11,127,65,106,168,27,175,56,5,57,8,104,178,185,198
    ,135,237,69,94,241,201,204,245,253,149,39,158,88,223,50,119
    ,41,216,17,221,40,213,64,103,249,161,126,76,59,18,202,219
    ,6,46,251,187,220,37,132,250,182,141,159,85,142,136,166,93
    ,230,58,31,155,97,215,90,197,144,30,150,48,109,139,177,174
    ,53,84,131,217,28,140,146,4,52,89,210,99,205,248,172,47
    ,246,234,102,244,240,196,157,79,44,225,25,181,154,108,134,224
    ,20,228,32,189,242,222,63,38,147,9,101,227,3,23,243,211
    ,110,156,66,125,91,200,193,164,71,68,83,160,115,29,129,195
    ,190,229,45,236,72,15,75,24,184,203,214,87,148,42,207,226
    ,14,70,73,2,26,162,105,191,232,124,86,153,123,117,51,122
    ,120,98,192,169,22,254,130,212,77,54,67,112,10,114,16,208
    ,121,111,145,19,199,138,188,255,143,133,247,231,55,78,33,176
    ,163,100,238,82,173,34,167,80,183,128,206,239,95,252,152,118
    ,36,137,171,12,92,235,107,165,74,21,233,113,7,35,170,1]
prodTbl2_toExp =
    [0,0,179,140,103,25,64,252,27,137,204,17,243,1,176,165
    ,206,50,61,211,128,249,196,141,167,122,180,22,100,157,89,82
    ,130,222,229,253,240,69,135,42,52,48,173,7,120,162,65,111
    ,91,14,46,190,104,96,201,220,24,26,81,60,13,12,6,134
    ,54,19,146,202,153,34,177,152,164,178,248,166,59,200,221,119
    ,231,2,227,154,97,75,186,171,44,105,86,148,244,79,35,236
    ,15,84,193,107,225,138,114,55,28,182,20,246,125,92,144,209
    ,203,251,205,156,5,189,239,47,192,208,191,188,185,147,58,18
    ,233,158,198,98,70,217,126,32,77,241,213,93,101,73,76,216
    ,88,210,102,136,172,41,90,11,238,187,124,83,145,118,43,74
    ,155,57,181,224,151,247,78,230,21,195,254,242,110,228,95,23
    ,223,94,29,9,10,123,72,232,168,30,3,67,214,131,160,183
    ,194,150,8,159,117,87,31,212,149,37,62,169,38,108,234,174
    ,207,4,106,143,199,53,170,85,49,99,16,63,68,51,133,45
    ,127,121,175,139,129,161,80,219,184,250,113,245,163,33,226,235
    ,116,36,132,142,115,39,112,218,109,56,71,66,237,40,197,215]


hoge = do
  i <- (0..255)
  let
    tmp = do
      j <- (0..255)
      case prodTbl2_fromExp !! j of
        Just y ->
          if i == y then
            pure $ j
          else
            []
        Nothing -> []
  if length(tmp) >= 1 then
    case (tmp !! 0) of
      Just z  -> pure $ z
      Nothing -> pure $ 0
  else
    pure $ 0


isPrimitiveElm_GF256 :: GF256 -> Boolean
isPrimitiveElm_GF256 x =
  (#) (Tuple 1 one) $ foldr ($) (const false) $
    replicate 255 $ \rec (Tuple i current) ->
      if current*x == one then
        i == 255
      else
        rec $ Tuple (i+1) (current*x)


data GF2 = Zero_GF2 | One_GF2

instance Show GF2 where
  show a =
    case a of
      Zero_GF2 -> "0_GF2"
      One_GF2  -> "1_GF2"

instance Eq GF2 where
  eq a b =
    case (Tuple a b) of
      -- 0 == 0 = True
      (Tuple Zero_GF2 Zero_GF2) -> true
      -- 0 == 1 = False
      (Tuple Zero_GF2 One_GF2)  -> false
      -- 1 == 0 = False
      (Tuple One_GF2 Zero_GF2)  -> false
      -- 1 == 1 = True
      (Tuple One_GF2 One_GF2)   -> true


instance Semiring GF2 where
  add a b =
    case (Tuple a b) of
      -- 0 + 0 = 0
      (Tuple Zero_GF2 Zero_GF2) -> Zero_GF2
      -- 0 + 1 = 1
      (Tuple Zero_GF2 One_GF2)  -> One_GF2
      -- 1 + 0 = 1
      (Tuple One_GF2 Zero_GF2)  -> One_GF2
      -- 1 + 1 = 0
      (Tuple One_GF2 One_GF2)   -> Zero_GF2
  zero = Zero_GF2

  mul a b =
    case (Tuple a b) of
      -- 0 * 0 = 0
      (Tuple Zero_GF2 Zero_GF2) -> Zero_GF2
      -- 0 * 1 = 0
      (Tuple Zero_GF2 One_GF2)  -> Zero_GF2
      -- 1 * 0 = 0
      (Tuple One_GF2 Zero_GF2)  -> Zero_GF2
      -- 1 * 1 = 1
      (Tuple One_GF2 One_GF2)   -> One_GF2
  one = One_GF2

addInv_GF2 c =
  case c of
    Zero_GF2 -> Zero_GF2
    One_GF2  -> One_GF2

mulInv_GF2 c =
  case c of
    Zero_GF2 -> Zero_GF2 -- ダミー
    One_GF2  -> One_GF2

instance Ring GF2 where
  sub a b = add a (addInv_GF2 b)

instance CommutativeRing GF2

instance EuclideanRing GF2 where
  degree = const one
  div a b = mul a (mulInv_GF2 b)
  mod = const zero

instance DivisionRing GF2 where
  recip = mulInv_GF2



zipForPolynomial :: forall a b. Semiring a => Semiring b => Array a -> Array b -> Array (Tuple a b)
zipForPolynomial xs ys = zip xs' ys'
  where
    xs' = (replicate (max (length xs) (length ys) - length xs) zero) <> xs
    ys' = (replicate (max (length xs) (length ys) - length ys) zero) <> ys

data PolynomialOverGF2 = PolynomialOverGF2(Array GF2)

delta_1 = PolynomialOverGF2([One_GF2,Zero_GF2])

instance Show PolynomialOverGF2 where
  show (PolynomialOverGF2 xs) = show xs

instance Eq PolynomialOverGF2 where
  eq (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) =
    (dropWhile (_ == zero) xs == dropWhile (_ == zero) ys)


instance Semiring PolynomialOverGF2 where
  -- 多項式同士の和
  add (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) = PolynomialOverGF2 $ dropWhile (_ == zero) do
    (Tuple x y) <- zipForPolynomial xs ys
    pure $ add x y
  zero = PolynomialOverGF2([])
  -- 多項式同士の積
  mul (PolynomialOverGF2 xs) (PolynomialOverGF2 ys) = foldr add zero $ do
      (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
      pure $ PolynomialOverGF2 $ do
        y <- (ys <> replicate n zero)
        pure $ mul x y
  one = PolynomialOverGF2(pure $ One_GF2)

addInv_PolynomialOverGF2 (PolynomialOverGF2 xs) = PolynomialOverGF2 $ do
  x <- xs
  pure $ addInv_GF2 x

instance Ring PolynomialOverGF2 where
  sub a b = add a (addInv_PolynomialOverGF2 b)

instance CommutativeRing PolynomialOverGF2

isZero_GF2 :: PolynomialOverGF2 -> Boolean
isZero_GF2 (PolynomialOverGF2 xs) = (xs == [])

getDegree_PGF2 :: PolynomialOverGF2 -> Int
getDegree_PGF2 (PolynomialOverGF2 xs) = max 0 (length (dropWhile (_ == zero) xs) - 1)
getCoeff_PGF2 :: PolynomialOverGF2 -> GF2
getCoeff_PGF2 (PolynomialOverGF2 xs) =
  case (xs !! 0) of
    Just fstElm -> fstElm
    Nothing     -> zero
genPolynomial_PGF2 :: Int -> GF2 -> PolynomialOverGF2
genPolynomial_PGF2 deg coe = PolynomialOverGF2 $ (pure coe) <> replicate deg zero

div_mod_PGF2 :: (Tuple PolynomialOverGF2 PolynomialOverGF2) -> Tuple PolynomialOverGF2 PolynomialOverGF2
div_mod_PGF2 (Tuple d1 d2) =
  (#) (Tuple zero d1) $ foldr ($) (const zero) $
    replicate (getDegree_PGF2 d1 + 1) $ \rec (Tuple res_div res_mod) ->
      let
        xs_deg = getDegree_PGF2 res_mod
        ys_deg = getDegree_PGF2 d2
        a      = getCoeff_PGF2 res_mod
        b      = getCoeff_PGF2 d2
        del    = xs_deg - ys_deg
      in
        if (del >= 0) && not(isZero_GF2(res_mod)) then
          let
            res_div' = res_div  + genPolynomial_PGF2 del (a*recip(b))
            res_mod' = res_mod - (genPolynomial_PGF2 del (a*recip(b)))*d2
          in
            rec(Tuple res_div' res_mod')
        else
          Tuple res_div res_mod

instance EuclideanRing PolynomialOverGF2 where
  degree = getDegree_PGF2
  div = curry(fst <<< div_mod_PGF2)
  mod = curry(snd <<< div_mod_PGF2)



data GF256 = GF256(PolynomialOverGF2)
prim = PolynomialOverGF2 [One_GF2,Zero_GF2,Zero_GF2,Zero_GF2,One_GF2,One_GF2,One_GF2,Zero_GF2,One_GF2]

quot :: PolynomialOverGF2 -> GF256
quot = GF256

isOne_GF256 :: GF256 -> Boolean
isOne_GF256 (GF256 x) =
  case (x `mod` prim) of
    (PolynomialOverGF2 zs) -> (zs == [One_GF2])      

instance Show GF256 where
  show (GF256 x) = show x

instance Eq GF256 where
  eq (GF256 x) (GF256 y) =
    (x `mod` prim) == (y `mod` prim)

instance Semiring GF256 where
  add (GF256 x) (GF256 y) = GF256 $
    (x + y) `mod` prim
  zero = (GF256 zero)
  mul (GF256 x) (GF256 y) = GF256 $
    (x * y) `mod` prim
  one = (GF256 one)

addInv_GF256 (GF256 x) = 
  GF256 $ addInv_PolynomialOverGF2 x

mulInv_GF256 x@(GF256 dat) =
  if isZero_GF2(dat) then
    zero
  else
    let
      ys = do
        d7 <- [Zero_GF2,One_GF2]
        d6 <- [Zero_GF2,One_GF2]
        d5 <- [Zero_GF2,One_GF2]
        d4 <- [Zero_GF2,One_GF2]
        d3 <- [Zero_GF2,One_GF2]
        d2 <- [Zero_GF2,One_GF2]
        d1 <- [Zero_GF2,One_GF2]
        d0 <- [Zero_GF2,One_GF2]
        pure $ GF256(PolynomialOverGF2(dropWhile (_ == zero) [d7,d6,d5,d4,d3,d2,d1,d0]))
      tbl = do
        y <- ys
        if isOne_GF256(x*y) then
          pure y
        else
          []
    in
      if length(tbl) == 1 then
        case tbl !! 0 of
          Just res -> res
          Nothing  -> zero
      else
        zero

instance Ring GF256 where
  sub a b = add a (addInv_GF256 b)

instance CommutativeRing GF256

instance EuclideanRing GF256 where
  degree = const one
  div a b = mul a (mulInv_GF256 b)
  mod = const zero

instance DivisionRing GF256 where
  recip = mulInv_GF256





data PolynomialOverGF256 = PolynomialOverGF256(Array GF256)

delta_1_256 = PolynomialOverGF256([one,zero])

instance Show PolynomialOverGF256 where
  show (PolynomialOverGF256 xs) = show xs

instance Eq PolynomialOverGF256 where
  eq (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) =
    (dropWhile (_ == zero) xs == dropWhile (_ == zero) ys)

instance Semiring PolynomialOverGF256 where
  add (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) = PolynomialOverGF256 $ dropWhile (_ == zero) do
    (Tuple x y) <- zipForPolynomial xs ys
    pure $ add x y
  zero = PolynomialOverGF256([])
  mul (PolynomialOverGF256 xs) (PolynomialOverGF256 ys) = foldr add zero $ do
      (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
      pure $ PolynomialOverGF256 $ do
        y <- (ys <> replicate n zero)
        pure $ mul x y
  one = PolynomialOverGF256([one])

addInv_PolynomialOverGF256 (PolynomialOverGF256 xs) = PolynomialOverGF256 $ do
  x <- xs
  pure $ addInv_GF256 x

instance Ring PolynomialOverGF256 where
  sub a b = add a (addInv_PolynomialOverGF256 b)

instance CommutativeRing PolynomialOverGF256

isZero_GF256 :: PolynomialOverGF256 -> Boolean
isZero_GF256 (PolynomialOverGF256 xs) = (xs == [])

getDegree_PGF256 :: PolynomialOverGF256 -> Int
getDegree_PGF256 (PolynomialOverGF256 xs) = max 0 (length (dropWhile (_ == zero) xs) - 1)
getCoeff_PGF256 :: PolynomialOverGF256 -> GF256
getCoeff_PGF256 (PolynomialOverGF256 xs) =
  case (xs !! 0) of
    Just fstElm -> fstElm
    Nothing     -> zero
genPolynomial_PGF256 :: Int -> GF256 -> PolynomialOverGF256
genPolynomial_PGF256 deg coe = PolynomialOverGF256 $ (pure coe) <> replicate deg zero

div_mod_PGF256 :: (Tuple PolynomialOverGF256 PolynomialOverGF256) -> Tuple PolynomialOverGF256 PolynomialOverGF256
div_mod_PGF256 (Tuple d1 d2) =
  (#) (Tuple zero d1) $ foldr ($) (const zero) $
    replicate (getDegree_PGF256 d1 + 1) $ \rec (Tuple res_div res_mod) ->
      let
        xs_deg = getDegree_PGF256 res_mod
        ys_deg = getDegree_PGF256 d2
        a      = getCoeff_PGF256 res_mod
        b      = getCoeff_PGF256 d2
        del    = xs_deg - ys_deg
      in
        if (del >= 0) && not(isZero_GF256(res_mod)) then
          let
            res_div' = res_div  + genPolynomial_PGF256 del (a*recip(b))
            res_mod' = res_mod - (genPolynomial_PGF256 del (a*recip(b)))*d2
          in
            rec(Tuple res_div' res_mod')
        else
          Tuple res_div res_mod

instance EuclideanRing PolynomialOverGF256 where
  degree = getDegree_PGF256
  div = curry(fst <<< div_mod_PGF256)
  mod = curry(snd <<< div_mod_PGF256)


fieldExt_GF2_GF256 :: GF2 -> GF256
fieldExt_GF2_GF256 x =
  quot(PolynomialOverGF2 [x])

assign :: PolynomialOverGF2 -> GF256 -> GF256
assign (PolynomialOverGF2 xs) a = foldr (+) zero $ do
  (Tuple n x) <- zip (reverse $ 0..(length xs - 1)) xs
  pure $ (fieldExt_GF2_GF256 x) * (foldr (*) one $ replicate n a)

タグ: プログラミング PureScript 小ネタ

タグ一覧:

物理学 (18)
古典力学 (9)
量子力学 (5)
数学 (56)
圏論 (32)
位相 (1)
線形代数 (7)
高校数学 (4)
プログラミング (28)
C言語 (4)
Haskell (32)
Java (1)
Python (2)
PureScript (3)
日記 (43)
小ネタ (17)
音楽 (4)
ピアノ (12)
ゲーム (18)
YouTube (36)

ページの先頭へ

TakuLabo

QR コードの仕様を学ぶ - 誤り訂正コード語の算出