雑記帳
「関数 f」と「値 f(x)」の違い
具体的な理由が挙げないと、「どうしてこんな抽象的でしょうもないことを考えなければいけないのか」とか、定番の「それやる意味ある」と思われて即おしまいになりかねないので、まず最初に動機付けとなる「これらの違いをしっかりと認識できるようになることで得られるメリット」を幾つか紹介していく。
何故こんなことを明確化したいのか...
動機 #1
「微分・積分」で行われる記号操作の意味や、その記号操作に用いる記号自体の意味を正しく理解し、その上で「そういうものなのだ」としっかりと妥協できるようになることに繋がる。
漠然と「記号の意味」と言われてもパッとしないかもしれないので具体例を上げさせてもらうと、
漠然と「記号の意味」と言われてもパッとしないかもしれないので具体例を上げさせてもらうと、
■ \(1(9) = 9\) or \(1(9) = 1\)
1 という記号は「単なる数字」なのか、それとも「\(f(x)=1\) で定まるような定数関数」なのか
■ \(\frac{df}{dx}\) vs. \(f'\)
\(h(x)=(g(f(x))\) で定まるような \(f\) と \(g\) の合成関数 \(h\) の微分はしばしば \(h'(x) = f'(x)\cdot g'(f(x))\) と表すことがあるが、 \(f'(x)\) の微分表記ではなく \(\frac{d}{dx} f(x)\) の微分表記を使ってこの式を書き換えることはできないのか?そしてその際、\(f'(x)\) の関数 \(f\) は「\(x\)という名前の変数」で微分していることがわかるが、そもそも \(g'(f(x))\) 内の関数 \(g\) は「どの名前の変数」で微分されているのか?
といった類いのものを思い浮かべると良い。
微積はほぼ万人が学ぶことになる必修ともいえる単元であり、抽象数学をやらない人たちにも関係するという意味で、一つ目のメリットとして挙げさせてもらった。
このページでもこのメリットに焦点を当て、それらの違いを明らかにしていくことを試みる。
微積はほぼ万人が学ぶことになる必修ともいえる単元であり、抽象数学をやらない人たちにも関係するという意味で、一つ目のメリットとして挙げさせてもらった。
このページでもこのメリットに焦点を当て、それらの違いを明らかにしていくことを試みる。
動機 #2
微積からはちょっと進んだ内容にはなるが、線形代数学というものを学び始めて暫くすると「双対空間」という奇妙な概念に出くわすことになる。双対空間というものは簡単に云うと「写像のなす線形空間の一種」であるのだが、その空間をなすベクトルが「数」ではなく「関数 (正確には線形形式と呼ばれる種類の線形写像)」となる以上、それらの違いをしっかりと理解していないことは、その概念を理解する上で求められる必須条件の一つを欠くことを意味する。
僕個人の意見ではあるが、双対空間の話は線形代数学の中でも理解が困難な話の部類に属しているものと思われ、その知識が不足しているとかなりの立ち往生を食らう羽目になってしまう可能性がある。
僕個人の意見ではあるが、双対空間の話は線形代数学の中でも理解が困難な話の部類に属しているものと思われ、その知識が不足しているとかなりの立ち往生を食らう羽目になってしまう可能性がある。
あいうえお
率直にいえば、教科書通りに正しく微積を学んでいれば
「f(x)」という記号こそが「(変数x を含む) 関数」という意味を持つ記号であり、タイトルで与えられているようなxという記号が切り離された「f」という記号はナンセンス
という理解に落ち着くのではないかと思う。
その類いの理解に行き着いた場合「文字式」を直接関数として認識していることになるのだが、実のところその曖昧さを伴う認識のままでは「f」と「f(x)」をはっきりと区別することが難しく、もっと抽象的でありながら漠然としてない関数の定義付けが必要になる。
とはいえ、その流儀が常識として染み付いているとどういうことか分かりづらい可能性があるため、まずは「文字式」を関数として捉えていることを認知するところから始めよう。
H1:
「f(x)」という記号こそが「(変数x を含む) 関数」という意味を持つ記号であり、タイトルで与えられているようなxという記号が切り離された「f」という記号はナンセンス
という理解に落ち着くのではないかと思う。
その類いの理解に行き着いた場合「文字式」を直接関数として認識していることになるのだが、実のところその曖昧さを伴う認識のままでは「f」と「f(x)」をはっきりと区別することが難しく、もっと抽象的でありながら漠然としてない関数の定義付けが必要になる。
とはいえ、その流儀が常識として染み付いているとどういうことか分かりづらい可能性があるため、まずは「文字式」を関数として捉えていることを認知するところから始めよう。
H1:
H2:
文字式を関数と捉えていたということを認知ができただろうか?
続いて、関数の定義について
文字式を関数と捉えていたということを認知ができただろうか?
続いて、関数の定義について
余談
このようなラムダで定義される関数の実体は何なのかと思う人のために余談をしておくと、一つの解釈としては、「無限亜群のなす(∞,1)-圏を公理化する際に、その(∞,1)-圏が指数対象の構成をサポートすること、つまり「無限亜群という構造をもつ任意の2対象間のモルフィズムは常に無限亜群をなし、その圏の住人として存在すること」を認めるのだが、そのラムダで構成される関数というのは、その指数対象の一般化要素と捉えることができる。ちなみにその一般化要素のステージはその圏の終対象を採用するが、この件の場合、その終対象は「集合」ではなく無限亜群であり、例えば「(U-small) 集合全体からなる亜群」のその一般化要素を考える場合、同形な対象が全て一括で参照されることになる。
(考える→やっぱりボツ を繰り返しているのでまだ暫く時間がかかりそう)
関数 \(f\) はしばしば
\[
f(x) = 2x+1
\]
といった関数 \(f\) を特徴付ける関係式を与えることによって定義することがある。
それだけでなく、「関数 \(f(x)\)」と
あああ
微分や積分が少しわかりにくく感じる点の一つとしてこの「関数と関数の取る値の違いをしっかりと認識できていない」
あああ
Haskell を使ってかなり大雑把に与えるとするならば
d :: Floating a => (a -> a) -> (a -> a)
d f = \x -> (f(x + epsilon) - f(x)) / epsilon
where
epsilon = 0.001(あまりにも杜撰過ぎる実装と思うかもしれないけれど、ここでは単に「関数」と「関数の値」の違いを理解することが目的であり、ここではその辺の細かいことは気にしないようにしよう。)
「関数は値にもなり得る」
微分積分では「\(t\) で微分」とか「\(x\) で積分をとる」といった台詞を聞くと思うけれど、本来は「変数名」は重要ではない。
関数 \(f:{\mathbb{R}} \rightarrow {\mathbb{R}}\) に対して
関数 \(f:{\mathbb{R}} \rightarrow {\mathbb{R}}\) に対して
\[
\frac{df}{dt}
\]
偏微分についても、「1番目の入力側で微分」や「2番目の入力側で微分」
関数 \(f:{\mathbb{R}} \times {\mathbb{R}} \rightarrow {\mathbb{R}}\) に対して
関数 \(f:{\mathbb{R}} \times {\mathbb{R}} \rightarrow {\mathbb{R}}\) に対して
\[
\begin{align}
\partial_1 f &:= {\rm uncurry}(\lambda a . d(\lambda x.f(x,a))) \\
\partial_2 f &:= {\rm uncurry}(\lambda a . d(\lambda x.f(a,x))) \\
\end{align}
\]
但し、
\[
{\rm uncurry}(f) = \lambda z.((f({pr}_1(z)))({pr}_2(z)))
\]
圏論的には \('f':1 \rightarrow (C^B)^A\) としたとき、\({\rm uncurry}('f'):1 \rightarrow C^{A\times B}\) は次のように定義できる
\[
\begin{align}
{\rm uncurry}('f') &:= {\rm arrToEl}(({\rm elToArr}('f') \times id) {\sf \, ⨟ \,} ev) \\
{\rm elToArr}('f') &:= \langle {\rm const}('f'), id \rangle {\sf \, ⨟ \,} ev \\
{\rm arrToEl}(f) &:= \lambda[{pr}_2 {\sf \, ⨟ \,} f] \\
{\rm const}(x) &:= \, ! {\sf \, ⨟ \,} x \\
\end{align}
\]
d1 :: Floating a => ((a,a) -> a) -> ((a,a) -> a)
d1 f = uncurry(\a -> d (\x -> f(x,a)))
d2 :: Floating a => ((a,a) -> a) -> ((a,a) -> a)
d2 f = uncurry(\a -> d (\x -> f(a,x)))\(f(x,y) = \cos(x) + x\cdot \sin(y)\) としたとき、通常の表記で「\(f\) を \(x\) で偏微分した関数」を表す場合
\[
\frac{\partial f}{\partial x}
\]
であるが、\(f(x,y) = \cos(x) + x\cdot \sin(y)\) は \(f(b,a) = \cos(b) + b\cdot \sin(a)\) というように定義することもでき、特に関数をラムダを使って定義してしまうと「変数名からどちら側の入力を指しているのかを遡ること」というのは基本的にできなくなる。
初めから番号で与えてしまえば、以下のように柔軟に微分を
\[
\begin{align}
\partial_1 f &= \partial_1 (\lambda(x,y).(\cos(x) + x\cdot \sin(y))) \\
&= \partial_1 (\lambda(b,a).(\cos(b) + b\cdot \sin(a))) \\
&= \lambda(b,a).(-\sin(b) + \sin(a)) \\
&= \lambda(x,y).(-\sin(x) + \sin(y)) \\
\end{align}
\]
blah
prod x y = x >>= (\el -> zip (repeat el) y)
blah
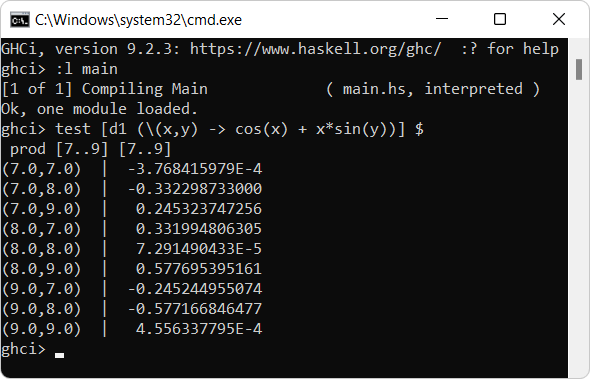
例えば \((-\sin(x) + \sin(y))\) は \(x=y\) であれば常に 0 だが、先ほど Haskell で定義したなんちゃって偏微分で実際にそれっぽい値が得られるかを確認してみよう
test [d1 (\(x,y) -> cos(x) + x*sin(y))] $ prod [7..9] [7..9]
上のコードを実行し、ターゲットとなる関数に対して7から9までの範囲内にある整数を \(x\) と \(y\) のそれぞれの変数に代入した値を調べてみると以下のような出力が得られるが、 \(x=y\) となる \((x,y)=(7,7),(8,8),(9,9)\) の点の値は全て0に近い値がしっかりと出力されていることを確認することができる。
あああ
infixl 6 +++
(+++) :: Floating a => (x -> a) -> (x -> a) -> (x -> a)
f +++ g = \x -> f(x) + g(x)
infixl 7 ***
(***) :: Floating a => (x -> a) -> (x -> a) -> (x -> a)
f *** g = \x -> f(x) * g(x)関数リスト内のそれぞれの関数に、値リスト内の全ての値を代入して得られる出力を描画するIOアクションを生成する関数
test :: Show a => [a -> Double] -> [a] -> IO ()
test fncs vals = foldr (>>) doNothing $ do
let
vals_Str = (fmap $ fmt . show) . take maxNumOfVals $ vals
domainWidth' = min domainWidth . maximum $ (fmap length) vals_Str
(x,x_Str) <- zip vals vals_Str
return $ do
let
listOfTabChrs = replicate (length fncs - 1) tabChr ++ [""]
listOfOutputs = fmap (\(f,s) -> (showFloat $ f x) ++ s) $ zip fncs listOfTabChrs
tmp1 = take domainWidth' $ x_Str
tmp2 = replicate (domainWidth' - length tmp1) ' ' ++ tmp1
putStrLn $ foldr (++) "" ((tmp2 ++ " | "):listOfOutputs)
where
maxNumOfVals = 100
domainWidth = 50
width = 15
trimLength = 7
errMsg = "ERROR"
tabChr = replicate 7 ' '
doNothing = ((return ()) :: IO ())
strToInt = takeWhile (`elem` ['0'..'9'] ++ ['-'])
strToUIntEnd = reverse . takeWhile (`elem` ['0'..'9']) . reverse
dropEnd = \i -> reverse . drop i . reverse
fix f =
let x = f x in x
showFloat = \u ->
if isNaN u || isInfinite u then
let
msgLength = length errMsg
tmp1 = (width - msgLength) `div` 2
tmp2 = (width - msgLength) - tmp1
in
(replicate tmp1 '-') ++ errMsg ++ (replicate tmp2 '-')
else
let
dataTbl = do
let
u' = (if 0 <= u then "+" else "-") ++ (show $ abs u) ++ "e0"
(j,c) <- zip [0..] u'
if c `elem` ['0'..'9'] ++ ['.','+','-','e'] then
if j == 0 then
if c == '-' then
return [c]
else
return " "
else
case c of
'.' ->
[ strToUIntEnd . take j $ u'
, show $ j-2 ]
'e' ->
[ strToUIntEnd . take j $ u'
, strToInt . drop (j+1) $ u' ]
_ -> []
else
[]
finalized =
let
sign = dataTbl!!0
xs = dataTbl!!1 ++ dataTbl!!3 ++ replicate width '0'
exponent = read $ dataTbl !! if length dataTbl == 5 then 2 else 4
expStr = show exponent
(xs', param1, param2, param3) =
if exponent < 0 then
( replicate (abs exponent) '0' ++ xs
, width - 1
, 0
, "" )
else if exponent <= width - 2 then
( xs
, width - 1
, exponent
, "" )
else
( xs
, width - 2 - length expStr
, 0
, "E" ++ expStr )
tmp = take param1 $ do
(j,c) <- zip [0..] xs'
if j == 1 + param2 then
'.' : return c
else
return c
in
sign ++ tmp ++ param3
in
finalized
fmt x =
let
tmp1 = scanText x
tmp2 = (fmap $ \(t,v)-> if t then (f v) else v) tmp1
f = trimDigit . dropWhile (==' ') . showFloat . read
in
foldr (++) "" tmp2
trimDigit x =
let
x' = x ++ "\0"
initVals = ([],0,0,0,'\0',False,False)
f = curry . fix $ \rec (current,(tmp1,num,cnt,decPlace,lastDigit,flg,rounded)) ->
case current of
[] ->
tmp1 >>= (\c -> if c=='\0' then [] else return c)
x:xs ->
let
loop = curry rec $ xs
params =
if x `elem` ['0'..'9'] then
let
num' = num*10 + read [x]
(param1,param2) =
if decPlace == 0 then
(num',0)
else if decPlace `elem` [1..trimLength] then
if lastDigit == x then
(num',succ cnt)
else
(num',1)
else
(num,cnt)
param3 = if decPlace > 0 then 1 else 0
(param4,param5) =
if decPlace <= trimLength then (x,False) else
if decPlace == trimLength+1 && x `elem` ['5'..'9'] then
(lastDigit,True)
else
(lastDigit,rounded)
in
(tmp1,param1,param2,decPlace+param3,param4,True,param5)
else
let
num' = num + if rounded then 1 else 0
numStr = show $ num'
pre =
if cnt > 0 then
case lastDigit of
'0' ->
dropEnd cnt $ numStr
'9' ->
if rounded then
dropEnd cnt $ numStr
else
numStr
_ ->
numStr
else
numStr
final =
let
strLen = length numStr
decPlace' = min trimLength $ pred decPlace
above = take (strLen-decPlace') pre
below = drop (strLen-decPlace') pre
in
if num' == 0 then "0" else
if null below then
above
else
if null above then
"0." ++ below
else
above ++ "." ++ below
in
if flg && x == '.' then
(tmp1,num,0,1,'\0',False,False)
else
if lastDigit == '\0' then
(tmp1 ++ [x],0,0,0,'\0',False,False)
else
(tmp1 ++ final ++ [x],0,0,0,'\0',False,False)
in
loop(params)
in
f x' $ initVals
scanText x =
let
x' = x ++ "\0"
initVals = (0,0,False,[],[])
f = curry . fix $ \rec (current,(flg1,flg2,flg3,tmp1,tmp2)) ->
case current of
[] ->
tmp1
x:xs ->
let
loop = curry rec $ xs
blah = abs flg1
blah2 = (flg1 == 0)
(param0,param1,param2) =
if x == '-' then
(blah,-1,flg3)
else if x `elem` ['0'..'9'] then
if flg2 == -1 then (blah,1,blah2) else (blah,0,blah2)
else if x `elem` ['.','e'] then
if flg3 then (blah,0,True) else (blah,0,False)
else if x =='\"' then
if flg1 <= 0 then
(1,flg2,flg3)
else
(0,flg2,flg3)
else if x =='\\' then
(-flg1,flg2,flg3)
else if x == '\0' then
(blah,0,not flg3)
else
(blah,0,False)
(param3,param4) =
if param1 == (-1) then
(tmp1,tmp2)
else
let
x' = [x] ++ (if param1 == 1 then "-" else "")
in
if flg3 == param2 || null tmp2 then
(tmp1,x'++tmp2)
else
(tmp1++[(flg3,reverse tmp2)],x')
in
loop(param0,param1,param2,param3,param4)
in
f x' $ initValsaaa
合成関数の微分
\[
\begin{align}
d(g \circ f) &= df \cdot (dg \circ f) \\
\end{align}
\]
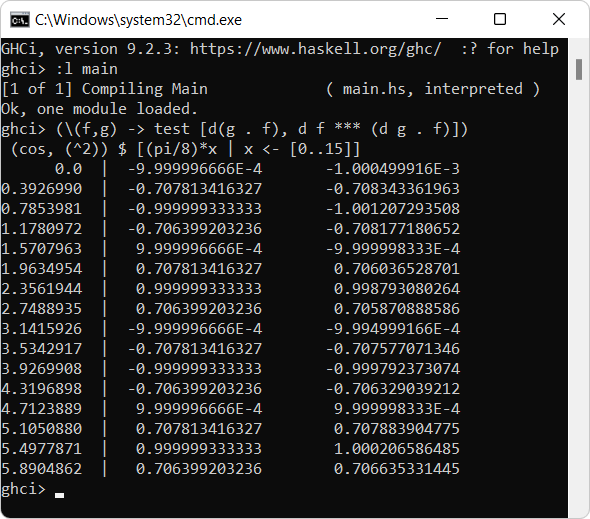
(\(f,g) -> test [d(g . f), d f *** (d g . f)]) (cos, (^2)) $ [(pi/8)*x | x <- [0..15]]
合成関数 \((-)^2 \circ \cos\) の微分
\[
\begin{align}
d((-)^2 \circ \cos) &= d(\cos) \cdot (d((-)^2) \circ \cos) \\
&= d(\lambda a.(\cos(a))) \cdot (d(\lambda a.(((-)^2))(a)) \circ \cos) \\
&= d(\lambda a.(\cos(a))) \cdot (d(\lambda a.(a^2)) \circ \cos) \\
&= (\lambda a.(-\sin(a))) \cdot ((\lambda a.(2a)) \circ \cos) \\
&= \lambda x.(((\lambda a.(-\sin(a))) \cdot ((\lambda a.(2a)) \circ \cos))(x)) \\
&= \lambda x.((\lambda a.(-\sin(a)))(x) \cdot ((\lambda a.(2a)) \circ \cos)(x)) \\
&= \lambda x.(-\sin(x) \cdot (\lambda a.(2a))(\cos(x))) \\
&= \lambda x.(-\sin(x) \cdot 2 \cos(x)) \\
&= \lambda x.(-2\sin(x) \cdot \cos(x)) \\
&= {\rm const}(-2) \cdot \sin \cdot \cos \\
\end{align}
\]
関数の取る値同士の積によって定まる関数の微分
\[
\begin{align}
d(f \cdot g) &= df \cdot g + f \cdot dg \\
\end{align}
\]
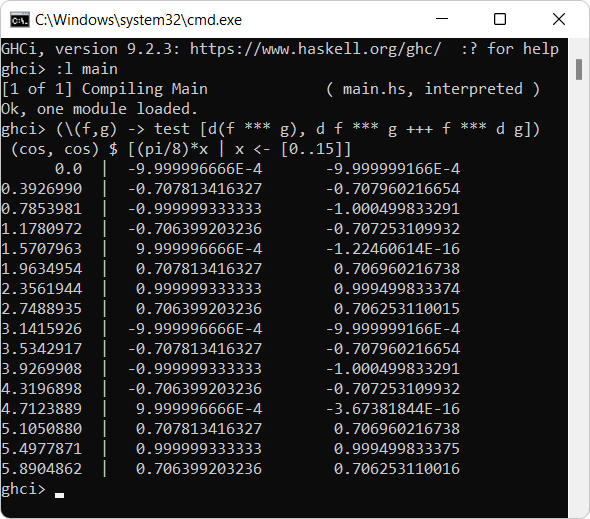
(\(f,g) -> test [d(f *** g), d f *** g +++ f *** d g]) (cos, cos) $ [(pi/8)*x | x <- [0..15]]
関数 \(\cos \cdot \cos\) の微分
(比較しやすいように、合成関数で挙げた例と同じ関数にしてある)
(比較しやすいように、合成関数で挙げた例と同じ関数にしてある)
\[
\begin{align}
d(\cos \cdot \cos) &= d(\cos) \cdot \cos + \cos \cdot d(\cos) \\
&= {\rm const}(2)\cdot(d(\cos) \cdot \cos) \\
&= {\rm const}(2)\cdot({\rm const}(-1) \cdot \sin) \cdot \cos \\
&= {\rm const}(-2) \cdot \sin \cdot \cos \\
\end{align}
\]
aaa
test [const 29] [return (), print 2, do{x <- getLine;putStrLn "blah";}]
命令型言語の場合、
純粋関数型言語であるため、リスト内にあるIOアクション (状態トランスフォーマ) は指定の識別子である main が与えられたアクションを生成する
アクション内で
タグ一覧:
