雑記帳
Euler–Lagrange 方程式を圏論的にネチネチと厳密に書いてみる 【小ネタ】
前置き
まず第一に、この記事はネタ記事です。
また「圏論的に」という部分について少し補足しておくと、別に「極限や随伴のような洗練された圏論的抽象概念を用いる」というわけではなくて、単に「集合ではなく射に焦点を当てる」という意味合いで使っている。
因みに「射に焦点を当てる」ということに一体どういったうれしさがあるのかといえば、
- 射に注目して記述する場合、曖昧な記述が難しくなり、見えづらかったことがくどいほどに可視化される。
ということである。
例えば、式を射の合成の形でしっかりと書き下すことによって「何処で何が起きているのか」を見失いづらくすることができる。
まあ前置きでグダグダと話し続けていても仕方ないので、どういうことなのかについては本題部分で確認していってほしい。
本題
まず「Euler–Lagrange 方程式」がやっていることを抽象的に捉える。
英語版 Wikipedia に書いてあることを要約すると、
Euler–Lagrange 方程式とは、
- \(X\): 滑らかな \(n\) 次元多様体 (\(U(X)\) を多様体 \(X\) の基底集合とする)
- \(TX\): \(X\) の接束
- \(z_a, z_b:1\rightarrow U(TX)\): \(TX\) 上の2点
- \(\langle [a,b], i_{[a,b]}\rangle\): \({\mathbb{R}}\) の部分集合
- \(L:[a,b]\times U(TX)\rightarrow {\mathbb{R}}\): ラグランジアン
とした時、
- \(c:[a,b]\rightarrow U(TX)\): \(c(a)=z_a\), \(c(b)=z_b\) を満たす接束 \(TX\) 上の任意の滑らかな曲線
に対して
\[
\int_a^b L(t,c(t)) dt
\]
によって定められる実数が極小となるような \(c\) を求める方程式。(多分)
因みに
- \(\langle {\rm Im}(c), i_{{\rm Im}(c)}\rangle\): \(c\) の像
- \(\langle U, i_U\rangle\): \(i_{{\rm Im}(c)} = (\subseteq){\sf \, ⨟ \,} i_U\) を満たすような写像 \((\subseteq):{\rm Im}(c)\rightarrow U\) が存在するような \(TX\) の開部分集合
- \(\varphi:U\rightarrow {\mathbb{R}}^n\times {\mathbb{R}}^n\): 接束 \(TX\) の持つ適当なチャート
とし、曲線 \(c\) を \({\mathbb{R}}^n\times {\mathbb{R}}^n\) 上に持っていって考えると、\((\varphi \circ c)(t)\) は \(\langle \boldsymbol{q}(t), \frac{d \boldsymbol{q}}{dt}(t) \rangle\) と書けるので、そのチャートの適当な選択の上で
\[
\int_a^b L(t,c(t)) dt
\]
は
\[
\int_a^b \bar{L}(t, \boldsymbol{q}(t), \frac{d \boldsymbol{q}}{dt}(t)) dt
\]
に置き換えられる。
余談
一般の多様体 \(X\) の接束 \(TX\) 上の点について、そもそもとして多様体上の点は一般に線形空間の構造を持たないため、何らかのチャートを使って \({\mathbb{R}}^m\) の点に変換してあげない以上「位置の成分表示」はできない。
つまり後者の式になってやっと \(\boldsymbol{q}(t)\) の成分表示が一般にできるようになる。
例の方程式を「写像の合成」を明示的に用いて書き換えてみる。
続いて、例の方程式
\[
\frac{\partial L}{\partial q_i}(t,\boldsymbol{q}(t),\dot{\boldsymbol{q}}(t)) - \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}(t,\boldsymbol{q}(t),\dot{\boldsymbol{q}}(t)) = 0
\]
を射に注目しながら書き換えてみる。(正直前節は Wikipedia の説明にちょっと手を加えただけの単なるおまけで、こちらがメインである。それと添え字の上下についてはここでは意味を持たせていない。)
まず、
\[
\begin{align}
\frac{\partial f}{\partial t}(t) &= (\partial f)(t) \\
\frac{\partial L}{\partial t}(t,\boldsymbol{x},\boldsymbol{v}) &= (\partial_{1} L)(t,\boldsymbol{x},\boldsymbol{v}) \\
\frac{\partial L}{\partial x_i}(t,\boldsymbol{x},\boldsymbol{v}) &= (\partial_{2i} L)(t,\boldsymbol{x},\boldsymbol{v}) \\
\frac{\partial L}{\partial v_i}(t,\boldsymbol{x},\boldsymbol{v}) &= (\partial_{3i} L)(t,\boldsymbol{x},\boldsymbol{v}) \\
\end{align}
\]
として左辺を整理すると
\[
\begin{align}
&\frac{\partial L}{\partial q_i}(t,\boldsymbol{q}(t),\dot{\boldsymbol{q}}(t)) - \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}(t,\boldsymbol{q}(t),\dot{\boldsymbol{q}}(t)) \\
=\:& \frac{\partial L}{\partial q_i}(t,\boldsymbol{q}(t),(\partial\boldsymbol{q})(t)) - \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}(t,\boldsymbol{q}(t),(\partial\boldsymbol{q})(t)) \\
=\:& \left(\frac{\partial L}{\partial q_i}\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle\right)(t) - \frac{d}{dt}\left( \left(\frac{\partial L}{\partial \dot{q}_i}\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle\right)(t) \right) \\
=\:& \left(\frac{\partial L}{\partial q_i}\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle\right)(t) - \left( \partial \left(\frac{\partial L}{\partial \dot{q}_i}\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle\right) \right)(t) \\
=\:& ((\partial_{2i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle)(t) - ( \partial ((\partial_{3i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle))(t) \\
=\:& ((\partial_{2i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle - \partial ((\partial_{3i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle))(t) \\
\end{align}
\]
よって
\[
(\partial_{2i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle - \partial ((\partial_{3i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle) = 0
\]
となる。
逆にわかりにくくなったと感じる人もいるかもしれないが、こちらのスタイルで書かれたものはそのまま Haskell コードに書き落とすことができる。
これについてはおまけとして紹介するので興味があればぜひ。
おまけ
Haskell を使ってWikipedia の例題を数値的に調べてみる
Wikipedia の例としてラグランジアンが
\[
L(t,x,v) = \sqrt{1 + v^2}
\]
で与えられたときの方程式の解 \(q\) が、次の関係式を満たす曲線 \(c\)
\[
c(t) = At + B
\]
になることが説明されている。
ということは、実際にその曲線を方程式に代入すれば当然、次の関数
\[
(\partial_{2i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle - \partial ((\partial_{3i}L)\circ\langle {\rm id}, \boldsymbol{q}, \partial\boldsymbol{q} \rangle)
\]
は定数関数 \(0\) になるということである。
ということで、実際にそれが \(0\) になっているのかを Haskell を使って大雑把に調べてみた。
ページ終わりに載せたコードを見れば意味がくみ取れると思うが、\(x_a\) と \(x_b\) を結ぶ4種類の曲線に対してそれぞれ上の関数を求め、その関数に-10 から 10 までの間の整数を全て代入して得られた値のリストを出力している。
因みに結果は以下のようになる。
ghci> main
#1:
[0.0,0.0,0.0,-8.881784197001252e-12,-8.881784197001252e-12,-8.881784197001252e-12,0.0,0.0,0.0,0.0,0.0,0.0,0.0,-8.881784197001252e-12,-8.881784197001252e-12,-8.881784197001252e-12,0.0,0.0,0.0,0.0,0.0]
#2:
[-5.503046907051612e-5,-7.837456905690487e-5,-1.1702582014549989e-4,-1.858966314216559e-4,-3.213470733953727e-4,-6.278179753849145e-4,-1.4879029741621252e-3,-5.007346288721237e-3,-3.8938748616601515e-2,-4.975810316838469,-3.6544267354443605e-2,-4.846381003176248e-3,-1.455668012795286e-3,-6.175693201271315e-4,-3.1713980774839e-4,-1.8386526079439136e-4,-1.1592860005293915e-4,-7.773095944685338e-5,-5.462865715344378e-5,-3.9844465504756954e-5,-2.9947884172543127e-5]
#3:
[2.4220980776590295e-6,4.36727987107588e-6,8.521681138518034e-6,1.8439720861351816e-5,4.595364089254872e-5,1.4054442942779133e-4,5.940772496160207e-4,4.521984653393929e-3,0.13386100597312378,-7.499565445989731e-2,-0.12210686672453619,-4.302668141775712e-3,-5.746244369220221e-4,-1.3707598611745198e-4,-4.504400408222864e-5,-1.813475591916358e-5,-8.40117309053312e-6,-4.312710188969504e-6,-2.3948132366058417e-6,-1.4154011296341196e-6,-8.787992555880919e-7]
#4:
[-2.3484184517030826e-2,9.744381301857175e-5,2.4969240817185323e-2,6.135734578736063,2.3606486028171503e-2,-9.781079057802344e-5,-2.5101209981670536e-2,-6.124455847031918,-2.3484184517030826e-2,9.744381301857175e-5,2.4969240817185323e-2,6.135734578736063,2.360648601928972e-2,-9.781079057802344e-5,-2.5101209999434104e-2,-6.124455847031918,-2.348418452591261e-2,9.744381301857175e-5,2.4969240826067107e-2,6.135734578736063,2.3606486028171503e-2]番号1のリストは、まさに方程式の解となる曲線に関するものであるのだが、見ての通り確かに「定数関数 0」っぽい感じになっていることがわかる。
わかりやすいように、-10 から 10 までの区間を 200 分割して得た値を用いて作成したグラフを以下に載せておく。
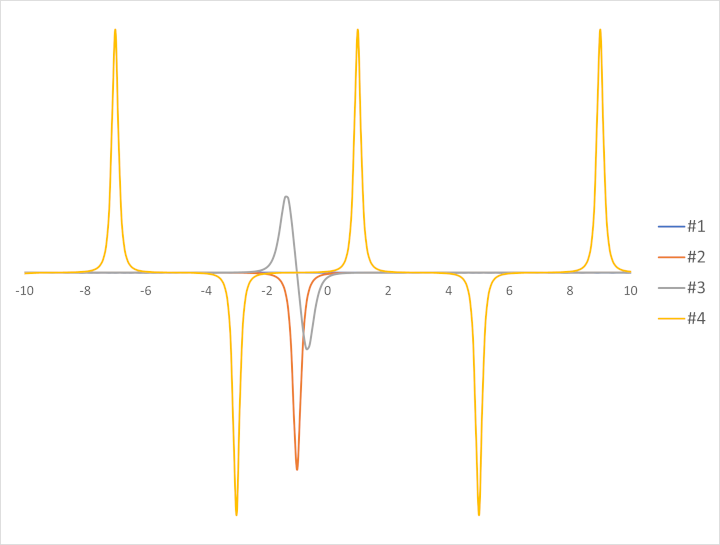
実際に解析的に求めた関数と比較して、「抽象的な関数の合成の形で書かれた式」によって知りたい関数が正しく得られているのかどうかを確認してみてほしい。
ソースコード
main :: IO ()
main = do
let
curves =
[ c_1
, c_2
, c_3
, c_s ]
foldr (>>) (return ()) $ do
(i,c) <- zip [1..] curves
return $ do
let
fnc = test lagrangian $ c
putStr $ "#" ++ show i ++ ":\n"
print $ do
t <- [-10..10]
return $ fnc(t)
putStr $ "\n"
a = -1
b = 1
x_a = 0
x_b = 10
c_1 = \t -> x_a + ((t-a)/(b-a)) * (x_b - x_a)
c_2 = \t -> x_a + ((t-a)/(b-a))^2 * (x_b - x_a)
c_3 = \t -> x_a + ((t-a)/(b-a))^3 * (x_b - x_a)
c_s = \t -> x_a + sin(pi/2*(t-a)/(b-a)) * (x_b - x_a)
test l = \q ->
((del_2 l).tuple3(id,q,del q)) `minus` (del((del_3 l).tuple3(id,q,del q)))
lagrangian ((t,x),v) = sqrt(1 + v^2)
espilon = 0.01
del f = \t ->
(f(t + espilon) - f(t))/espilon
del_1 f = \((t,q),q') ->
(f((t + espilon,q),q') - f((t,q),q'))/espilon
del_2 f = \((t,q),q') ->
(f((t,q + espilon),q') - f((t,q),q'))/espilon
del_3 f = \((t,q),q') ->
(f((t,q),q' + espilon) - f((t,q),q'))/espilon
pair = uncurry $ (<*>) . fmap (,)
tuple3 (f1,f2,f3) = pair(pair(f1,f2),f3)
minus f g = \t ->
f(t) - g(t)タグ一覧:
