雑記帳
Copilot は圏論的に構成された Haskell 関数の構造を上手く紐解けるのか？ 【余積編】
「ある射の純粋圏論的構成」を Haskell の Prelude 標準モジュールの関数たちを使って行い、そうして作った関数を Copilot に投げたらどんな出力が得られるのだろうかと気になったので、試してみることにした。
このコーナーで取り扱っていくのは、これまで扱ってきたような「わざとごちゃごちゃわかりにくく書いたコード」ではなく、その手の変な捻りの無い至って普通な「圏論的構成をそのままなぞって書き下しただけの関数」となるので、できれば良い意味で僕の期待の上をいく出力をいただきたいのだが…
今回は【余積編】ってことで、余積の考えがゴリゴリと使われる射の構成に対する Copilot の対応状況を見ていこう。
前置き
まずどうでもいい前置きになるけど、最初は「スタートラインに立つまでに労力を一切使わなくて済むようなコード」を Copilot に渡した方がいいのかなとちょっと悩んだわけです。
というのも、Haskell の標準モジュール関数を使った実装の形で展開・記述されている圏論的に意味を持った各まとまりを綺麗に整える作業を済ました先に、
\[
{\rm tw}{\sf \, ⨟ \,} \left( \left(\begin{matrix} \lambda[{\rm tw}{\sf \, ⨟ \,} {\rm inj}_1] \cr \lambda[{\rm tw}{\sf \, ⨟ \,} {\rm inj}_2] \end{matrix}\right) \times ((1+1)+1) \right){\sf \, ⨟ \,} {\rm ev} {\sf \, ⨟ \,} (((1+1)+1) + {\rm prj}_1) {\sf \, ⨟ \,} \left({\rm tw}{\sf \, ⨟ \,} \left( \left(\begin{matrix} \lambda[{\rm tw}{\sf \, ⨟ \,} {\rm inj}_1] \cr \lambda[{\rm tw}{\sf \, ⨟ \,} {\rm inj}_2] \end{matrix}\right) \times ((1+1)+1) \right){\sf \, ⨟ \,} {\rm ev} + ((1+1)+1)\right) {\sf \, ⨟ \,} (({\rm prj}_1 + {\rm prj}_1) + ((1+1)+1)) {\sf \, ⨟ \,} [[[[{\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1, {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1], {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1],[[{\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1, {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1], {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1]],[[{\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1 {\sf \, ⨟ \,} {\rm inj}_1, {\rm inj}_2 {\sf \, ⨟ \,} {\rm inj}_1], {\rm inj}_2]] {\sf \, ⨟ \,} (([[[[[[[[\langle \langle 0,0 \rangle, 0 \rangle,\langle \langle 0,1 \rangle, 1 \rangle],\langle \langle 0,2 \rangle, 2 \rangle],\langle \langle 1,0 \rangle, 1 \rangle],\langle \langle 1,1 \rangle, 2 \rangle],\langle \langle 1,2 \rangle, 0 \rangle],\langle \langle 2,0 \rangle, 2 \rangle],\langle \langle 2,1 \rangle, 0 \rangle],\langle \langle 2,2 \rangle, 1 \rangle]) {\sf \, ⨟ \,} {\rm prj}_2)
\]
といったスタートラインとなる構成式が見えてくるコードを渡すのですが、仮にもしそのスタートラインに立つまでの過程で躓かれてしまうと、本題となる「その構成が数学的にどういう意味であるのかの説明」以前の話で終わってしまうためです。
ってことでどうしようかと考えた結果、「いやでも莫大過ぎるエネルギーとコストを浪費しておきながら動かされているのが "わざわざユーザーがそういった配慮をしなければまともに機能してくれないポンコツ" であってはダメ」という結論に至り、結局通常通りの一行完結コードを渡すことになりました。
本題
さて無駄話が過ぎましたが、本題に入っていこう。
まず上述の原型を見れば察することができるように、従来の集合論の知識 (常識) に染まっているとまずやらない余積の使われ方が多く含まれていること、それから「(従来の集合論では写像の定義として与えているはずの) 写像のグラフ \(\Gamma_f \subseteq A\times B\)」と「写像 \(f:A\rightarrow B\)」それ自体とを明確に区別して考えておかないと理解しづらい構成を採用していることもあり、スタートラインに立ってからの意味の汲み取りがどれだけ適切にできているのかと、圏論的な視点がどれだけ身についているのかの繋がりが特に顕著に出てくるクイズでもあるでしょう。
つまりこのクイズは圏論ファンとしてのレベルを確認するのにもピッタリなわけです。
ってことで早速 Copilot さんがどれだけ圏論に夢中になっているのかを今からテストしていきましょう。
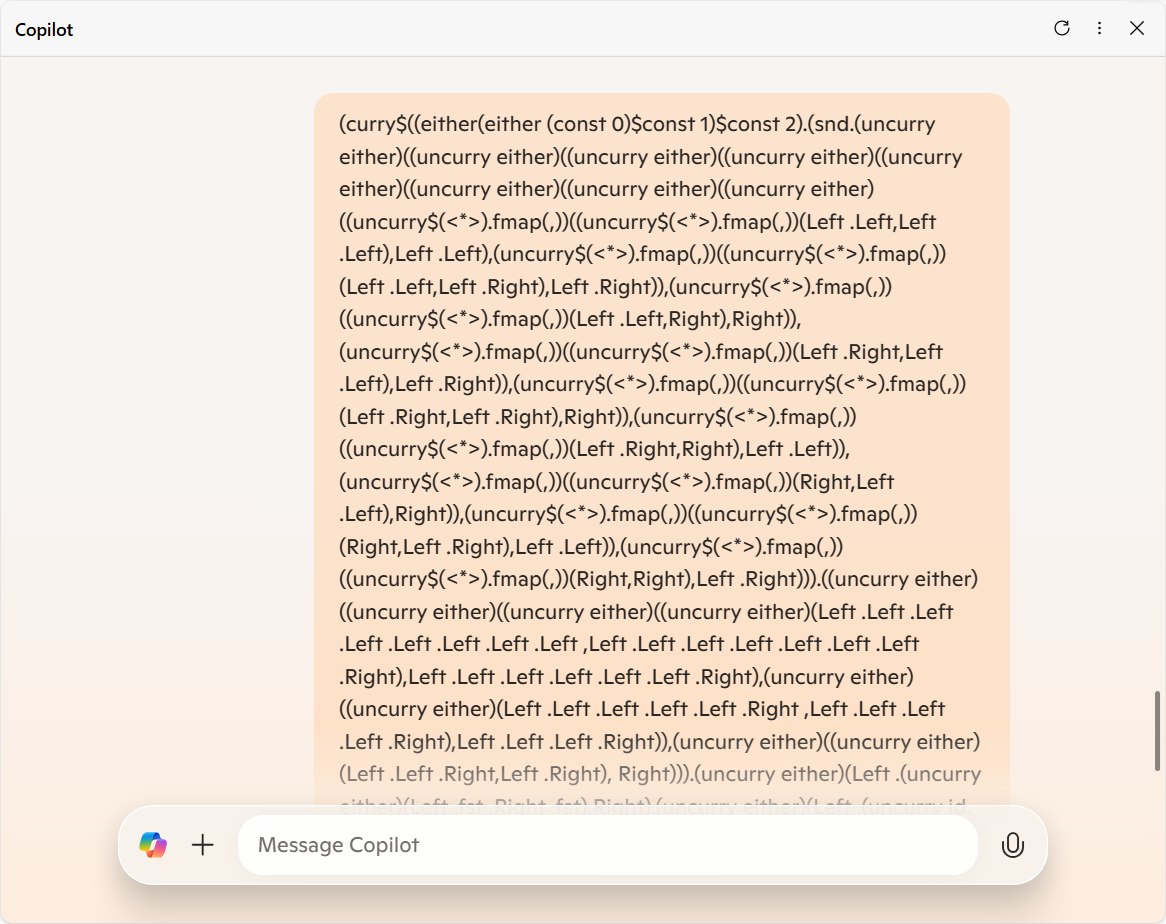
Copilot に渡したコードは以下。
(curry$((either(either (const 0)$const 1)$const 2).(snd.(uncurry either)((uncurry either)((uncurry either)((uncurry either)((uncurry either)((uncurry either)((uncurry either)((uncurry either)((uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Left,Left .Left),Left .Left),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Left,Left .Right),Left .Right)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Left,Right),Right)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Right,Left .Left),Left .Right)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Right,Left .Right),Right)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Left .Right,Right),Left .Left)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Right,Left .Left),Right)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Right,Left .Right),Left .Left)),(uncurry$(<*>).fmap(,))((uncurry$(<*>).fmap(,))(Right,Right),Left .Right))).((uncurry either)((uncurry either)((uncurry either)((uncurry either)(Left .Left .Left .Left .Left .Left .Left .Left ,Left .Left .Left .Left .Left .Left .Left .Right),Left .Left .Left .Left .Left .Left .Right),(uncurry either)((uncurry either)(Left .Left .Left .Left .Left .Right ,Left .Left .Left .Left .Right),Left .Left .Left .Right)),(uncurry either)((uncurry either)(Left .Left .Right,Left .Right), Right))).(uncurry either)(Left .(uncurry either)(Left .fst ,Right .fst),Right).(uncurry either)(Left .(uncurry id.(uncurry$flip(,)).(fmap$(uncurry either)(curry$Left .(uncurry$flip(,)),curry$Right .(uncurry$flip(,))))) ,Right).(uncurry either)(Left , Right .fst).(uncurry id.(uncurry$flip(,)).(fmap$(uncurry either)(curry$Left .(uncurry$flip(,)),curry$Right. (uncurry$flip(,))))).((uncurry$(<*>).fmap(,))(uncurry id.(uncurry$(<*>).fmap(,))(snd,fst.fst),uncurry id.(uncurry$(<*>).fmap(,))(snd,snd.fst)).(fmap$const$((!!)$(fmap.(flip id)$())[Left .Left, Left .Right,Right]).min 2)).(uncurry$(<*>).fmap(,))(id,const()))) 2 2
入力と出力の部分で整数と余積対象の要素とを結び付ける処理が組み込まれているものの、基本的に関数部分は上に載せた構成式をそのままなぞって書いたもので、その上でその関数に 2 と 2 を適用して得られる結果を出力させています。
2 と 2 を適用して得られる結果を出力させています。ちなみにこの関数の意味や導出過程は以下の記事を参照。
その記事を確認すればわかる通り、上のコードは 1 を出力します。
1 を出力します。実際 GHC で上のコードをコピペして実行してあげれば、確かに 1 が出力されることを自分自身で確認することもできるでしょう。
1 が出力されることを自分自身で確認することもできるでしょう。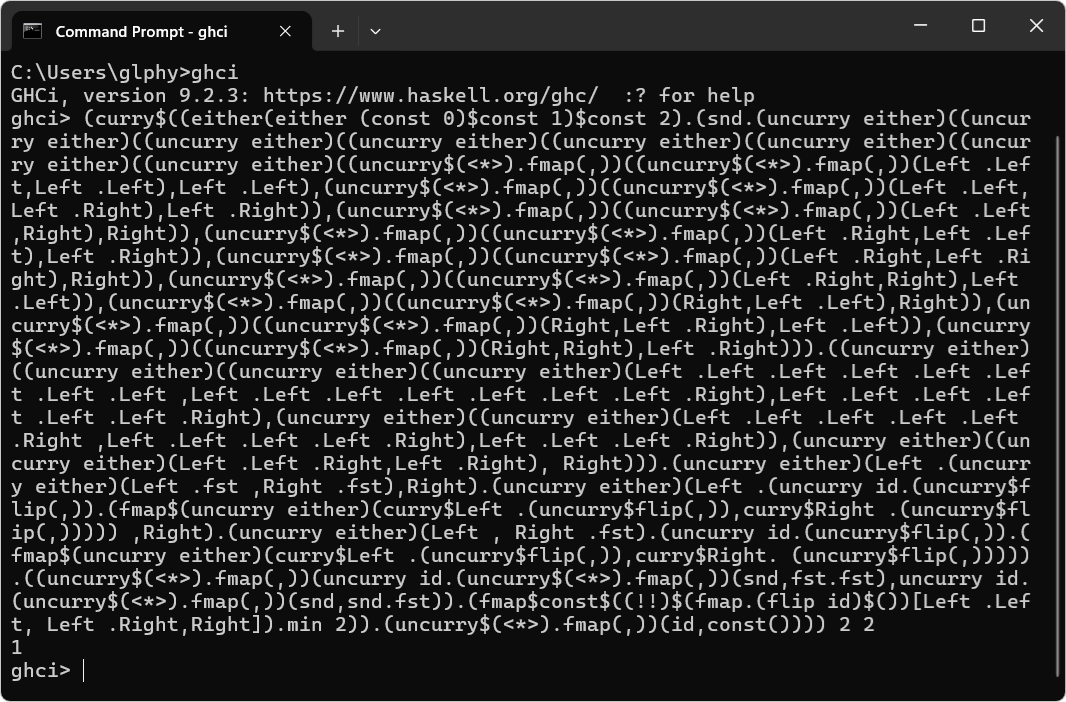
以上を踏まえたうえで、Copilot さんの出力を見ていきましょう。
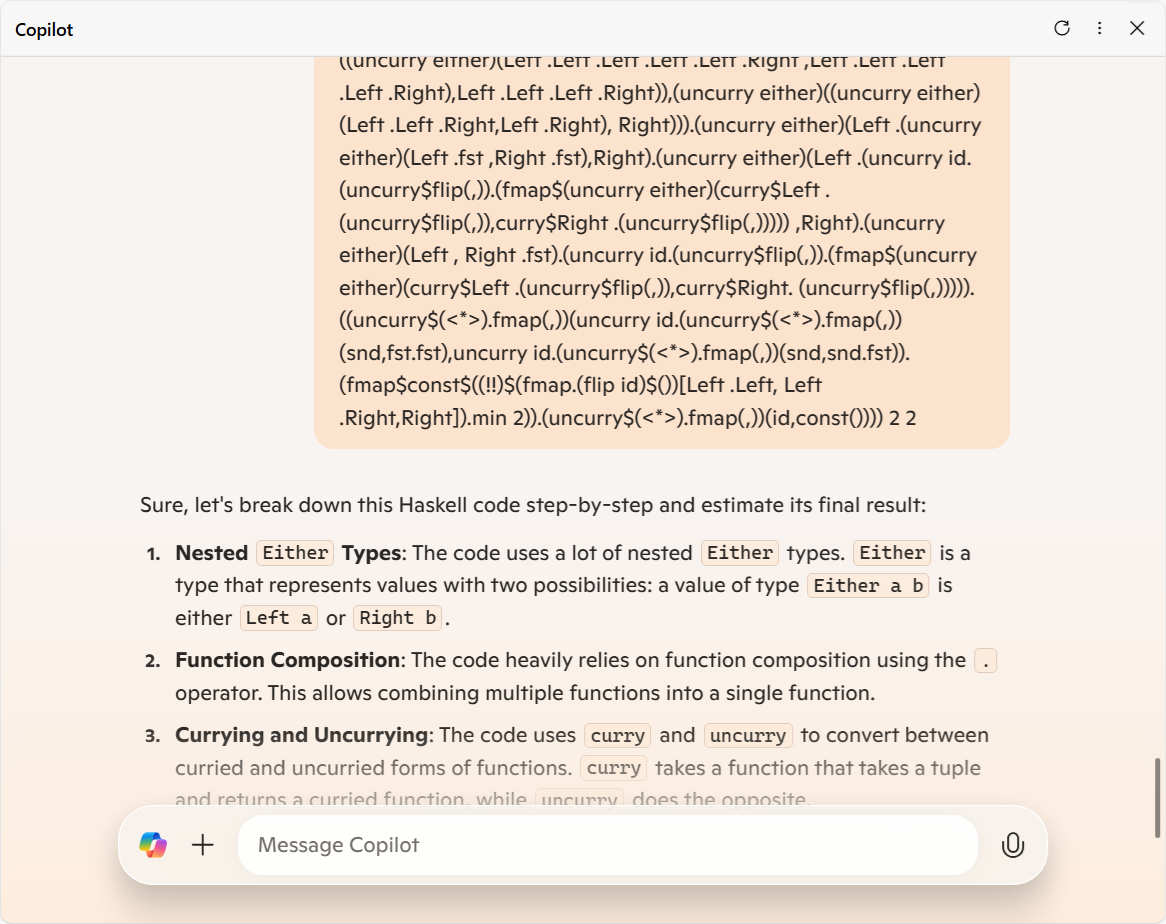
「Either 型の値に対するパターンマッチングのために either 関数を使っている」といった記述がありますが、その記述は圏論ファン失格の証よ。
Either 型の値に対するパターンマッチングのために either 関数を使っている」といった記述がありますが、その記述は圏論ファン失格の証よ。(Syntax-free な) 圏論的構成はそういった「パターンマッチング」をはじめとする表記上の形式的な記号操作への意味付けとしての側面もあり、その意味付けを与える構成の中で意味付けされる側に置いている記号操作の話を持ち出してしまうことは話の循環を引き起こすことに繋がってしまうし、最もやってほしくなかったことの一つでありました。
「余積対象であること以上の意味を見出さずに Either 型を捉えること」がポイントになるのだけど、今後統計的に優位な言葉の流れをたどっていった先に、非常識なやりかたを説明する上手い文章が仕上がる良いメソッドが編み出される未来を期待したいですね。
Either 型を捉えること」がポイントになるのだけど、今後統計的に優位な言葉の流れをたどっていった先に、非常識なやりかたを説明する上手い文章が仕上がる良いメソッドが編み出される未来を期待したいですね。それと「7: List Manipulation」で Copilot が幻を見ている点について補足させていただくと、「タプルのリストを作ってそのリスト内の全てのタプルに対して該当の関数を適用させる形の zip や repeat を含むコード」を先行して渡していたことが恐らく影響してしまったようです。(検証に使用するコードを取り替えたのは、単純に全然本題でないそのタプルのリストを作る箇所で変に躓かれてしまったためです。)
zip や repeat を含むコード」を先行して渡していたことが恐らく影響してしまったようです。(検証に使用するコードを取り替えたのは、単純に全然本題でないそのタプルのリストを作る箇所で変に躓かれてしまったためです。)一方、そのコード内で List comprehensions (リストの内包表記？) については一切登場していなかったので、そちらの幻覚に対しては正直僕も意味が分かりません。
最後に Copilot さんが最終出力をどのように予想したのかについて。
なんか今回は不可思議な理由を添えつつ「コードの分析をしたら、最終出力は 2 であるみたい (After analyzing the code, it appears that the final result of the code is 2.)」とおっしゃっています。(何をどのように *分析* を行ったらその結果に辿り着いてしまったのかはヒミツのようです)
2 であるみたい (After analyzing the code, it appears that the final result of the code is 2.)」とおっしゃっています。(何をどのように *分析* を行ったらその結果に辿り着いてしまったのかはヒミツのようです)最終部分をみればすぐわかるように出力は「0, 1, 2」の3択となるので、せっかくなら正解を引く Copilot さんを見たかったですね。
というのもハズレの値が当てはめられていると面白おかしく感じる説明文でも、そこが正解に置き換わると途端に「全てを見透かしてしまっている感」が醸し出てくるような魔法の文章になっているので。
視点を変えれば、本当言葉の連ね方が巧妙というか、ユーザーを欺くことに長けすぎているというか。
まとめ
Copilot さんや ChatGPT が非大卒の出した圏論クイズに適切に答えられるようにするためにも、ETCS 集合論についてかなり詳しく説明するネット記事が今後量産される未来を皆で願いましょう。
余談
この手の茶番記事は Copilot さんが改善されない限り続くと思うのでご了承を。
Lawvere 数学流行ってくれたらもちろん面白いのだけど、一度これまで学んできた数学を全面的に否定することになるので難しそうよな。
まあ流行らなければ流行らないで生成AIが充分にデータを取り込むことが難しい状況が続くわけで、その間ずっと珍回答を引き出す遊びができるから別にいいけども。
タグ一覧: