【検証】Haskell コードの構造は Copilot さんによって正しく解釈されるのか？【小ネタ】

main = ((foldr($)(return())).repeat$uncurry(>>).(uncurry$(<*>).fmap(,))(const$putStr "Please enter the word \"topos\"!\n>> ",uncurry(>>=).(uncurry$(<*>).fmap(,))(const getLine,(curry$(uncurry$(either(const fst)$const snd).([Left(),Right()]!!).fromEnum.not).(uncurry$(<*>).fmap(,))(uncurry(==).(uncurry$(<*>).fmap(,))(snd,const("topos")),(uncurry$(<*>).fmap(,))(const(putStrLn "perfection"),uncurry(>>).(uncurry$(<*>).fmap(,))(const $ putStr "Oops, you must've accidentally typed wrong one.\n\n",fst)))))))

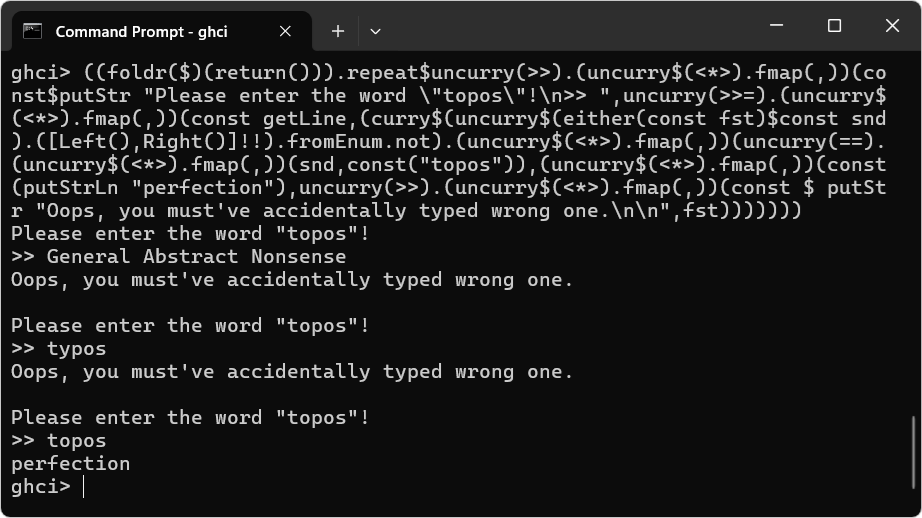
※Haskell というか関数型言語にあまりなじみがないと、こんなアホみたいなコードが動作するなんて考えられないと思うかもだけど、実際に GHC をインストールして実行させてみれば ↑ こんな感じに動作することの確認がとれるよ。

するとこんな回答が出力された。

一見すると、「このごちゃごちゃしたコードを理解できてんの？マジで？」と早とちりしてしまう人がいるかもだけど、ちょっと冷静に。

もし本当にコードの構造を把握出来ているのであれば、コードの構造とは無関係な「プログラムの意味を推測する手がかり」となり得る部分 (e.g. 出力させる文字列, 変数名・関数名のような識別子の与え方, コメント) を攪乱させても、変わらず頓珍漢でない出力が得られるはずである。

ということで続いては、「出力させる文字列の内容とコードの挙動とが合致していないトラップを仕組んだコード」を渡してみる。(コードの構造は冒頭のものと全く一緒で、出力する文字列だけが変更してある。※それと後から気付いたけど、「the word」を「any word」とか「an arbitrary word」とかに直し損ねてた)

main = ((foldr($)(return())).repeat$uncurry(>>).(uncurry$(<*>).fmap(,))(const$putStr "Please enter the word, which shouldn't be \"topos\"!\n>> ",uncurry(>>=).(uncurry$(<*>).fmap(,))(const getLine,(curry$(uncurry$(either(const fst)$const snd).([Left(),Right()]!!).fromEnum.not).(uncurry$(<*>).fmap(,))(uncurry(==).(uncurry$(<*>).fmap(,))(snd,const("topos")),(uncurry$(<*>).fmap(,))(const(putStrLn "You shouldn't. As I warned you earlier, any other word is welcome, but the word isn't."),uncurry(>>).(uncurry$(<*>).fmap(,))(const $ putStr "It's perfect. see'ya!\n\n",fst)))))))

するとどうでしょう。

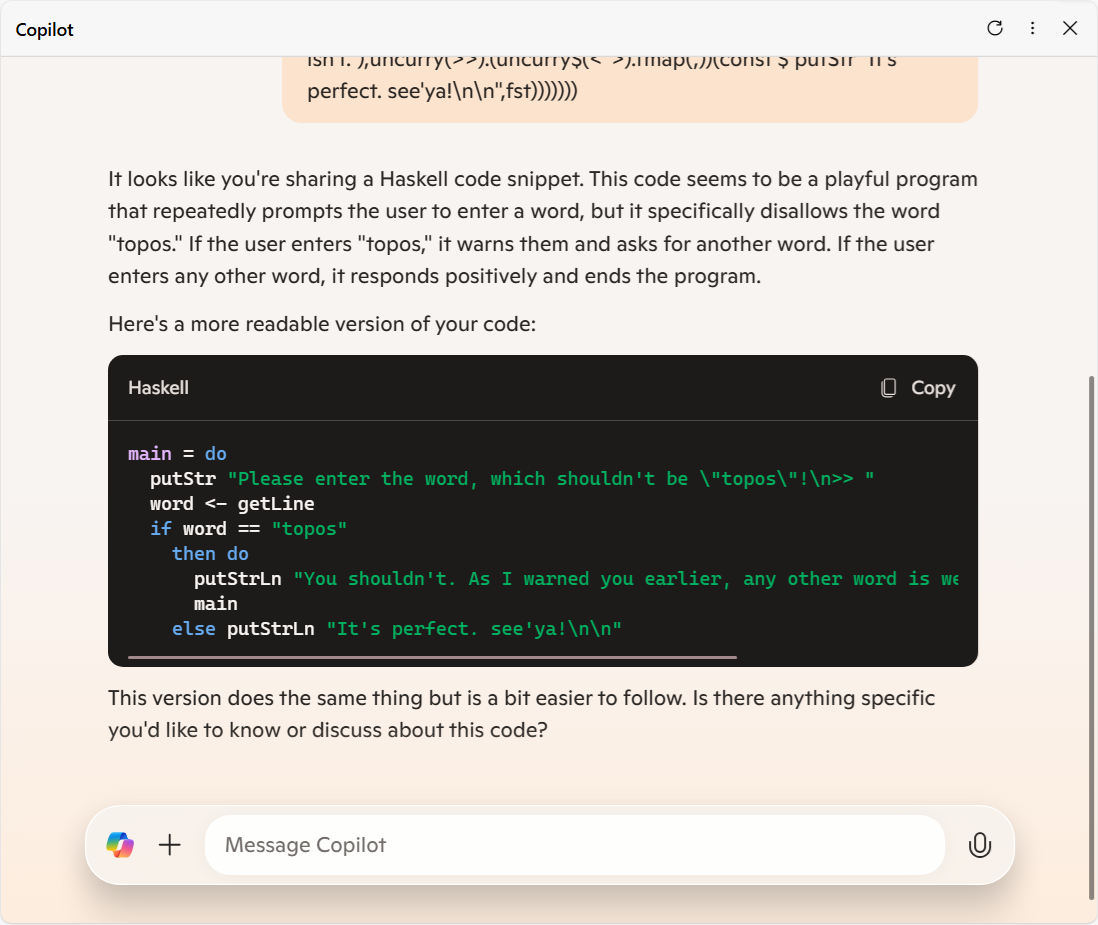
案の定、コードの構造は変えずに単に「文字列」を変えただけなのに、その文字列の意味に引っぱられた出力が得られました。

具体的には、「"topos" が入力されると停止するプログラム」なのに、「"topos" 以外が入力されると停止するプログラム」として解釈されています。

それになんと今回はその意味が真逆になった偽コードの出力特典付き。

main = do
  putStr "Please enter the word, which shouldn't be \"topos\"!\n>> "
  word <- getLine
  if word == "topos"
    then do
      putStrLn "You shouldn't. As I warned you earlier, any other word is welcome, but the word isn't."
      main
    else putStrLn "It's perfect. see'ya!\n\n"

結局は、コードそれ自体を把握しているわけではなくて、コード上に散らばっているヒントを統計的に継ぎ接ぎしているだけなのかしら？

今回は罠を仕掛けて遊んでいる体だからエンターテインメントとして楽しめるけど、この「入り組んだプログラムを読み解いて、さらに可読性の高いコードに書き換えるまでしてしまった」というパフォーマンスにみせかけた「コード内の断片的なヒントの上手な継ぎ接ぎ」は、ちょっと悪質かしら。

最後にオマケとして、予想が上手くいった後に、「コード内にある

Left()

はどうして必要なのか」を入力してみたら...

なんじゃこりゃ。

ちょっと何を言っているかわかりませんが、あてずっぽうが上手なことはわかりました。

率直にいうと、自明な「1」以外、もれなく全部違います。(

Either

型のよくある使用パターンに一切則らずにコードを書いているので、この場面ではその蘊蓄話が出てくること自体もちょっと筋違いなのかも)

何なら、その「1」ですらも、「

Left()

がこのコードにおいてどのような役割を持っているのか」を説明する上で、全く持ち出す必要のない非本質的な部分ではあるのですが...

実際のところは、「2, 3」の説明でしれっと使っている「IF 分岐」を与える構造

(Bool,(IO (),IO ())) -> IO ()

の構成の中で用いられているのであって、その分岐を終えた先にはもう

Left()

の役目はないし、

Left()

の値が作られるかどうかについても当然「その型の分岐関数が完成される前の話」になるので、判定式の結果に依りません。

加えて、「文字列が "topos" かどうか」を判定した後のそれぞれの分岐先として与えている値の型は上記の通り

IO ()

型であるわけですが、その部分も全然違う

Either a b

型の値として文章化してくれているのも嬉しくないですね。

ちなみにですが、仮に無理やり「値が作られる」を「値が評価される」という意味で捉えたとしても、この場面においては、その判定式の結果となる

Bool

型の値が

False

ではなく

True

の時に IF 分岐関数の内部で値

Left()

が評価されるような構造になっているので、いずれにせよ「入力が "topos" でない、つまり判定が

False

の時に、コードが

Left

の値を作り出す」という記述は正しいとはいえないです。

あとなんかトンデモな説明を長々としてくれていますが、第一に

Bool -> Int

型の関数である

fromEnum.not

に

Either () b

の値

Left()

を渡すことも当たり前だけどできないよね。

ケース2: 文字列の先頭と末尾の文字以外を切り落とす関数

ケース1に対して「そんなごちゃごちゃしたコードなら間違ってしまうのも致し方ないんじゃない？」と考える人もいると思うので、続いて「それなりに短くなるコード」の例として、Point-free スタイルで書いた「文字列の先頭と末尾以外の文字を切り落とす関数」を Copilot に入力してみる。

(flip(map.flip id)$[head,last])

結果は以下の通り

この短いコードでもここまで大胆に間違えることができるとは、なんとも恐ろしい。

何が恐ろしいって、ユーザーにステップバイステップで丁寧に誤った説明を提供しているところよね。

実はそのステップバイステップの説明自体が「見当違いなテキトーな文字列」でも、質の悪いことに「雰囲気それっぽくみえてしまう文章」であるわけだから、まだ分別のつかない初学者の中に「こんなに噛み砕いて説明できるということは、ちゃんとわかっているからこそだ」みたいな印象を植えつけられてしまう人がいてもおかしくないのかなと少し心配になる。

余談として「文字列の長さが 0 や 1 の場合にも対応できるようなコード」を敢えて Point-free でかつ、王道的な分岐の作り方を避けて書くとするならば、例えば

((uncurry$(flip maybe)(flip(map.flip id)$[head,last])).((fmap((uncurry(>>)).(uncurry((flip $ (,).foldr const Nothing . fmap Just . drop 1).return).((,)>>=id)))).((,)>>=id)))

といった感じで書くこともできるよ。

ちなみにこちらを Copilot に入力したところ、一切のありがたみのない分かりきった単調な事実の羅列が得られました。(具体的には、選択肢は１つに限られている中、「The exact behavior will depend on the specific monad and values involved.」みたいな文字列と共に、コード内で使われている幾つかの関数の説明文が出力されました。)

一応最後に、本題のコードの非大卒なりの説明も付け加えておく。

まず「与えられた文字列の先頭文字と末尾文字だけを取り出した文字列を作る関数」を作りたいとなったとき、Haskell においてそういった関数は、

(\str -> [head str, last str])

つまり、「引数として指定された文字列に対して、

head

と

last

それぞれを適用して得られる二つの文字からなるリストを作る関数」として組み立てられることに気付く。

あとは、このコードがどのようにして Point-free の形式で構成できるのかを考えてみればよい。

まず

head

と

last

の型が同じである、言い換えるとそれら2つの関数のリストを (余積の考えを持ち出すことなく) そのまま作ることができる点に着目する。

この点がわかれば、「特定の値を関数に適用する関数」を

map

に適用させることで「リスト内の全ての要素に同じ値を適用する関数」を作り、その上でそのリスト間の関数に「

head

と

last

を要素に持つリスト」を値として適用させれば欲しい関数が得られるという流れが見えてくる。

ではこの流れを押さえたうえで、その関数を構成するために必要となるピースを組み立てていく。

出発点となるピースは、「ある値に対して、その値を関数に適用する関数を作り出す関数」となる。

これについては Haskell をやった人なら、即座に

($)

のことが思い浮かんでくると思うが、せっかくなので数学的な観点からじっくり物事を考えてみよう。

まず圏論的に「値を適用する関数」というのは「評価射 ${\rm ev}:B^A\times A\rightarrow B$」のドメインの第2成分の型 $A$ の値を適用して得られる関数 $B^A\rightarrow B$ に該当する。

ここで、「ある値に対して、その値を関数に適用する関数を作り出す関数」というのは、よりフォーマルには「評価射について、第一成分側を拘束 (コドメイン側に移動) させ、第二成分側はそのまま自由に (ドメイン側に保持) させる形への作り変えを施した射」にあたる。

Haskell において、複数引数を持つ関数を扱う際に使用する

積対象をドメインに持つ関数 (A,B)->C
指数対象をコドメインに持つ関数 A->(B->C) (上のカリー化)

という2つのタイプの関数はおおよそ違いなきものとして扱われる慣習があり、それに従うとすると、評価射のカリー化は一般的抽象的ナンセンスより恒等射となる事実 (指数対象の普遍性から従う、評価射と対応する仲介射の一意性) より、Haskell において評価射

(A->B,A)->B

というのは単に

(A->B)->(A->B)

という型の恒等関数と同一視できる。

とはいえ、恒等関数としてみた評価射は「

側の入力が拘束されていて、

A->B

側の入力が自由である (

がコドメイン側にいて、

A->B

がドメイン側にいる)」という状況であり、今欲しい「

側の入力が自由になっていて、

A->B

側の入力が拘束されている (

がドメイン側にいて、

A->B

がコドメイン側にいる)」という状況とは「拘束されている入力と自由になっている入力との関係性」がちょうど真逆になっている。

さてどうしようかと思うかもしれないが、ちょうどこの関係性を反転させたい目的を果たすのにピッタリな関数が Prelude 標準モジュールには備わっていて、それが

flip

関数になる。

つまり欲しい関数である「ある値に対して、その値を関数に適用する関数を作り出す関数」は、単に「

flip id

」というシンプルな形で構成されることになる。

余談

Copilot さんは、そういった圏論的な背景を一切無視してなんかその関数は「essentially the identity function」という一言で片づけてしまっていますが、実のところは、Haskell の慣習上見えづらくはなっているけど、評価射の意味合いで使われています。

これで、「ある値に対し、その値を適用する関数を出力する関数」が得られたので、あとはそうして得られることになる「特定の値を適用する関数」をそのまま

map

関数に投げてしまうことで、「与えられた関数を指定のリスト内の要素全体に適用する関数の取得」へと繋げていけばよい。

ここまでを纏めると、「ある値に対し、その値を与えられたリスト内の全ての要素に適用する関数」というのが「

map.(flip id)

」として得られることがわかったわけである。

だいぶ完成に近づいてきたが、次に考えたいのは関数のリスト

[head,last]

を先の関数に適用することだが、先の関数というのは「自由になっているのが "文字列の入力" で、"関数のリストの入力" は拘束されている」という状況にあり、そのまま関数のリストを適用できるフォーマットにはなっていない。

即ち、また

flip

を使って、自由になっている入力と拘束されている入力とを反転させる必要がある。

それらを反転させた後、リスト

[head,last]

をその関数に適用してあげれば、遂に欲しかった関数

[Char]->[Char]

」が無事に得られる。

以上、Copilot が生成してしまった「

(flip(map.flip id))[head,last]

は

[head,last]

になる」という説明のテキトーさがわかったかな？

ケース3: Point-free 版の min 関数

Point-free 版の min 関数を Copilot に入力した時の出力もなかなかに驚愕だったので、ここに追記しておく。

引数として入力した２つの数 a,b の内、小さい値の方の数を戻り値として出力する関数

min'

は

min' a b = if a < b then a else b

となるが、これは以下のように変数を使わずに構成し直すことができる。

min' = (curry$(uncurry$maybe fst(const snd).([Nothing,Just ()]!!).fromEnum.not).((<*>).fmap(,))(uncurry(<))id)

さて、この小さいほうの値を求める関数を使って、「3.1415926 と 2.7182818 のどちらが小さい数なのか」を調べてみる。

(curry$(uncurry$maybe fst(const snd).([Nothing,Just ()]!!).fromEnum.not).((<*>).fmap(,))(uncurry(<))id) 3.1415926 2.7182818

まず GHC に確認していただいたところ...

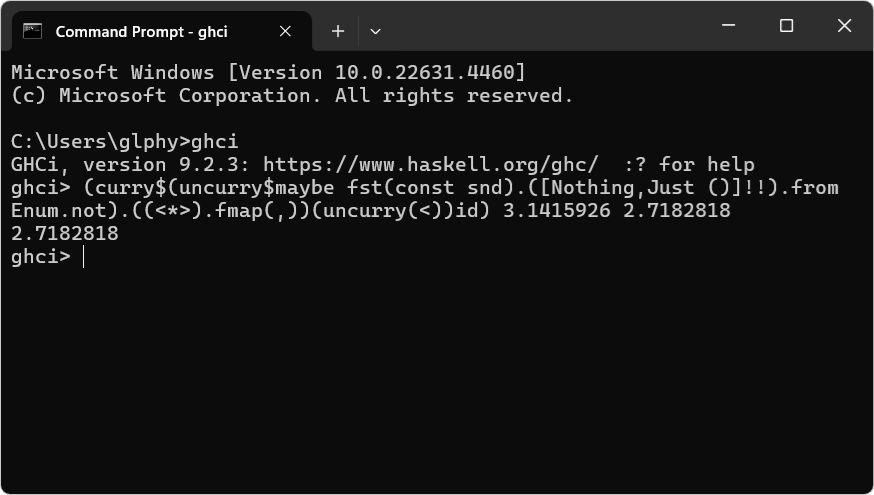
2.7182818

の方が小さいらしいです。

では続いて Copilot にこのコードを入力してみましょう。

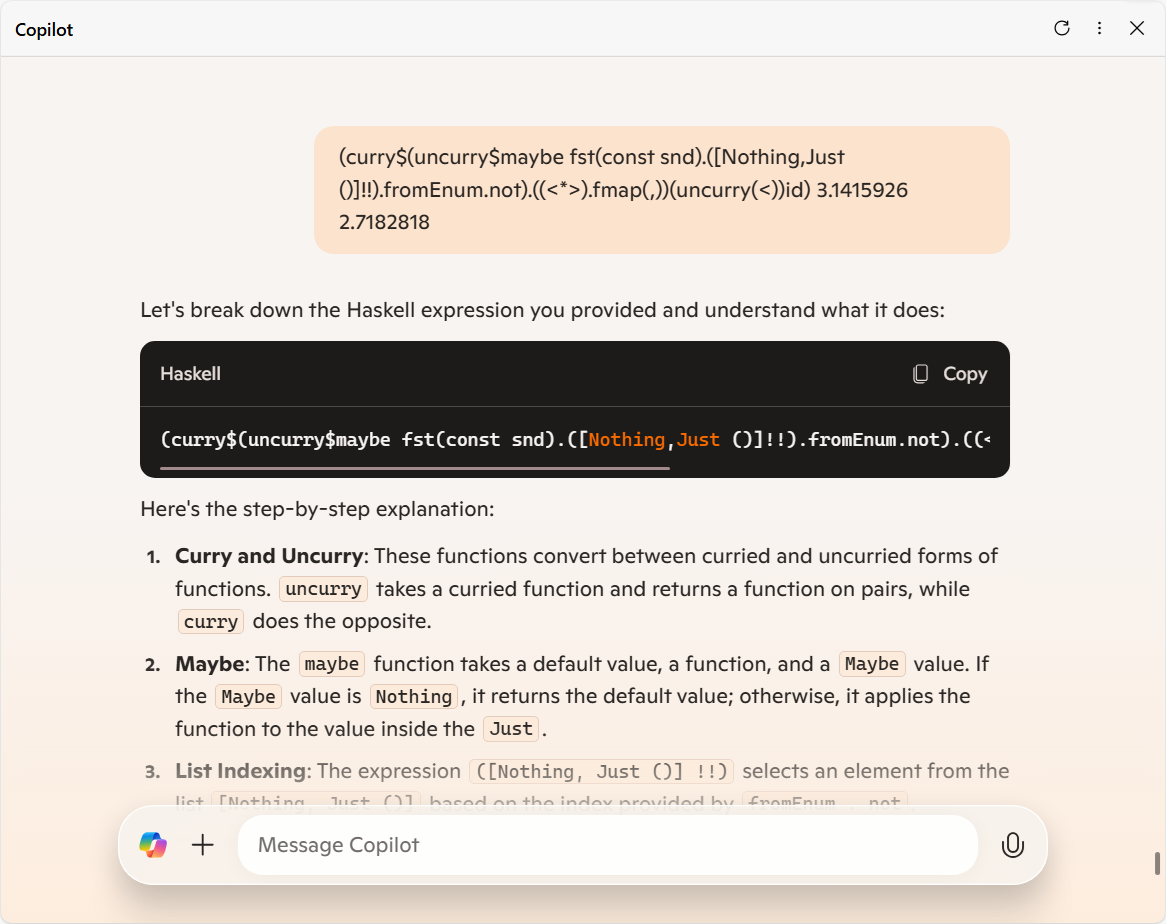
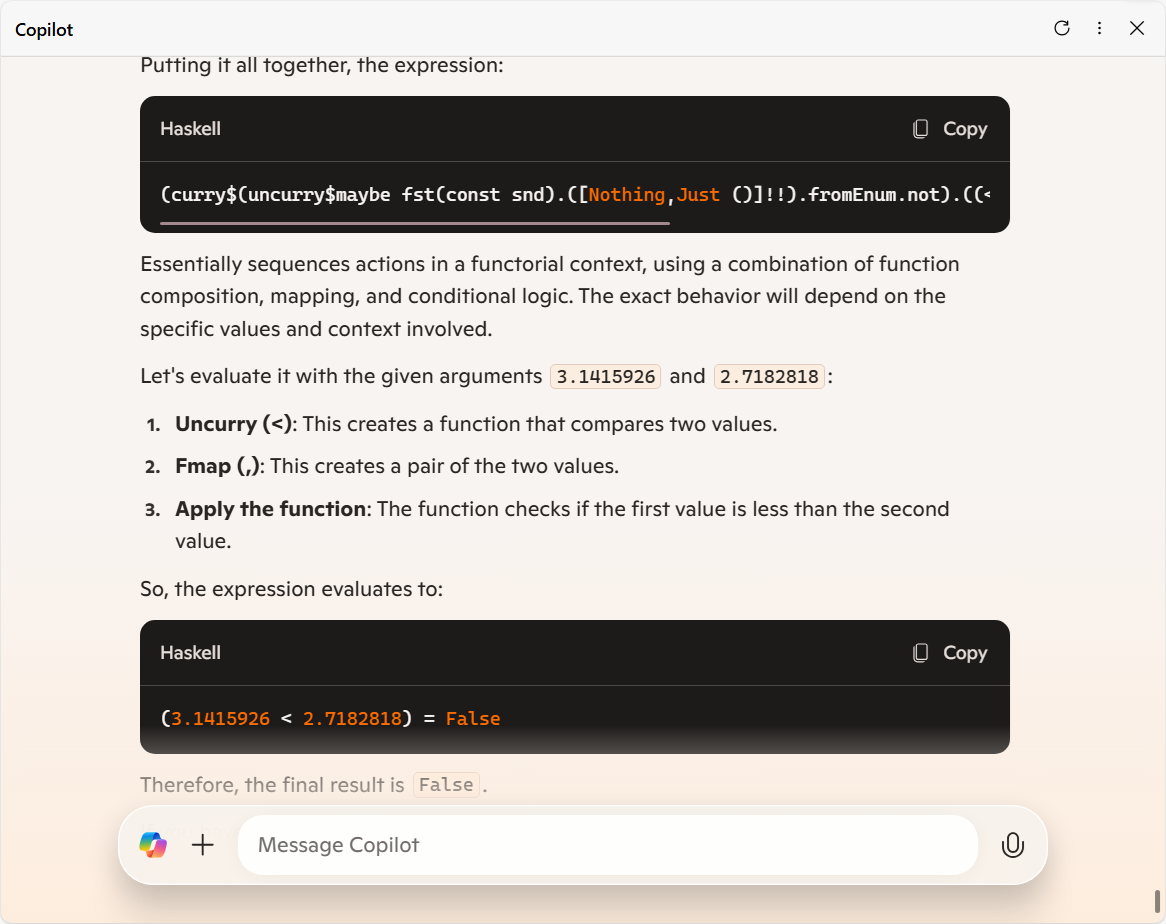
※ 途中の求めていない関数の説明文は一部省略

この様子なので、なんかより一層断片的な情報の上手な繋ぎ合わせとしてテキトーな文字列を生成しているんだなって部分を見て取れた気がします。

御覧の通り Copilot は、「3.1415926 と 2.7182818 のどちらが小さい値であるのか」を求めるコード

(curry$(uncurry$maybe fst(const snd).([Nothing,Just ()]!!).fromEnum.not).((<*>).fmap(,))(uncurry(<))id) 3.1415926 2.7182818

から余計な情報を削ぎ落してなんと

(<) 3.1415926 2.7182818

という (意味は全然変わってしまったけど) 可読性の高いコードに "最適化" してくれました。

(ちなみに、「2」の「Fmap (,)」の説明も自明な関手の場合を除いて一般に正しくなさそうなんだけど、LLM においては「意味が厳密に正しいかどうか」ではなく「文章が雰囲気それらしいか」が全てっぽいので、その手のツッコミはダメなのよね)

極端な言い換えをするならば、Copilot さん的には

min' a b = if a < b then a else b

というコードは

min' a b = a < b

と最適化できるとのことです。

もう何なのよコレ。

ケース4: 任意精度有理数を使った級数の計算

表題だけ見ると「単に Copilot が算術に対応しているのかどうかの検証」にも見えるがそうではなくて、ちゃっかり忍ばせてある「ぱっと見では意味がないように見えるけど、型の情報を与えている重要な部分」をしっかり注意深く捉えてくれるのかの検証を目的としている。

ちなみに Copilot に入力したコードは以下。

(\p numOfDigits -> let {_ = fromRational p;(x,q) = properFraction p} in (show x ++ "." ++ (show $ truncate(abs(q)*fromIntegral (10^numOfDigits))))) (sum $ (fmap $ \n -> 1 / (1+product[1..n]))[0..30]) 30

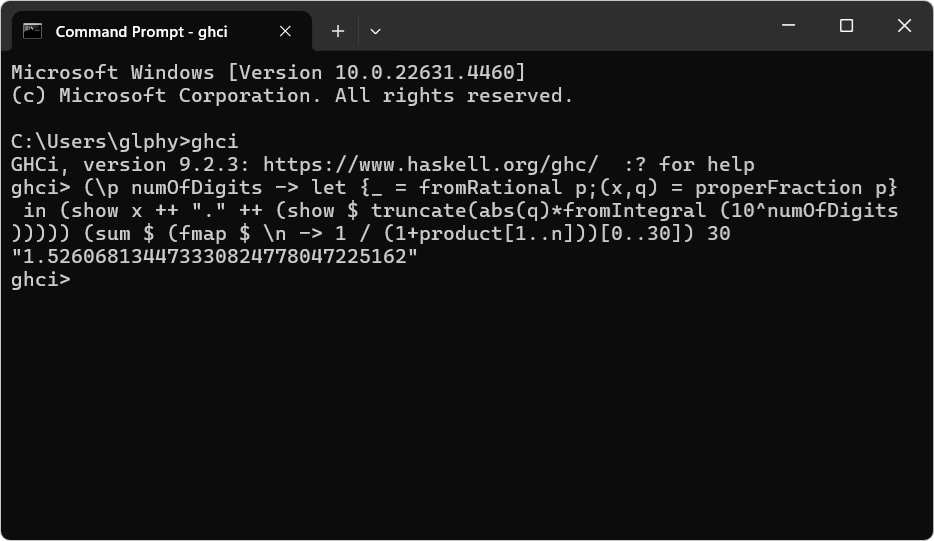
(↑ GHC に実行させた結果)

具体的にポイントとなるのが、

_ = fromRational p;

という部分で、

を任意精度有理数型

Rational

として型推論させているのだが、以下のように想像通りその辺がガバガバになっている出力が得られました。(※この部分がなくなると浮動小数点数を使って級数の計算が行われてしまうので、当然計算結果も変わります。)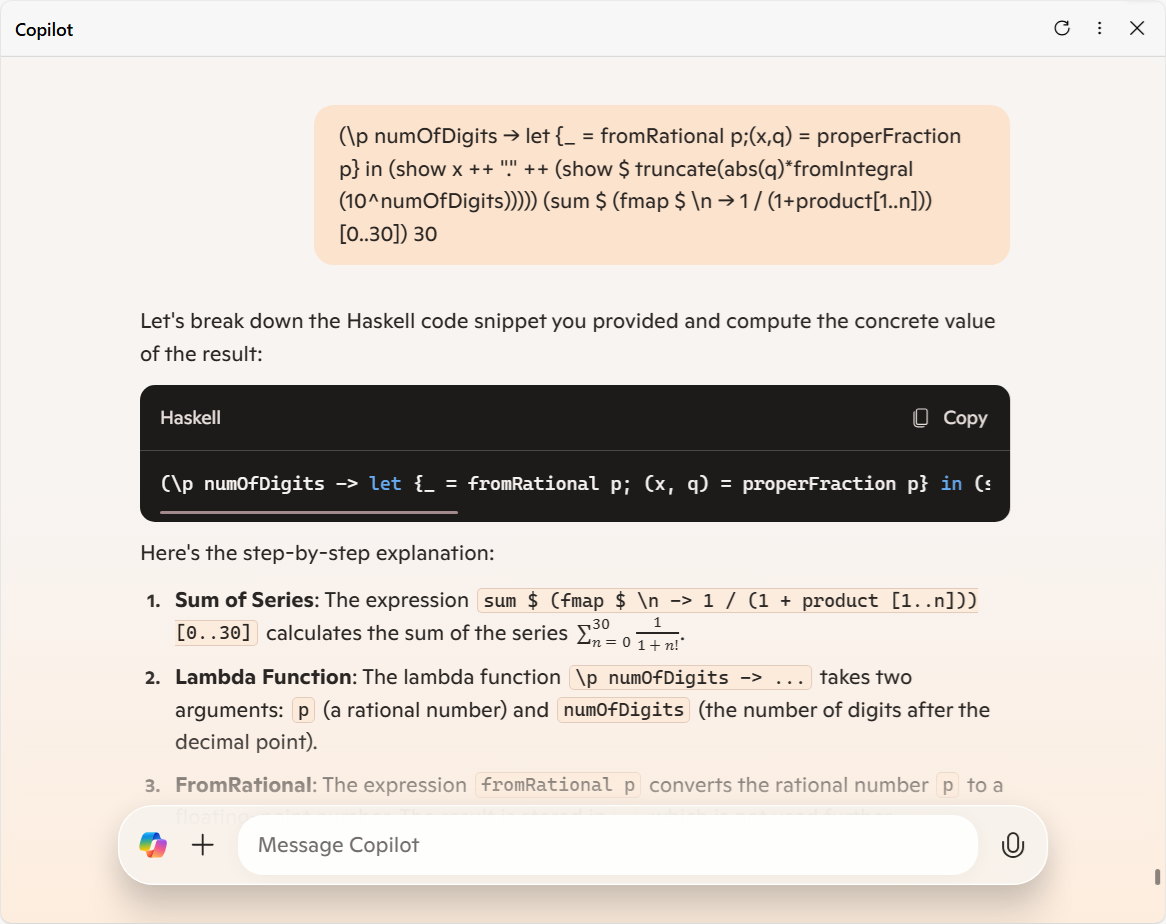

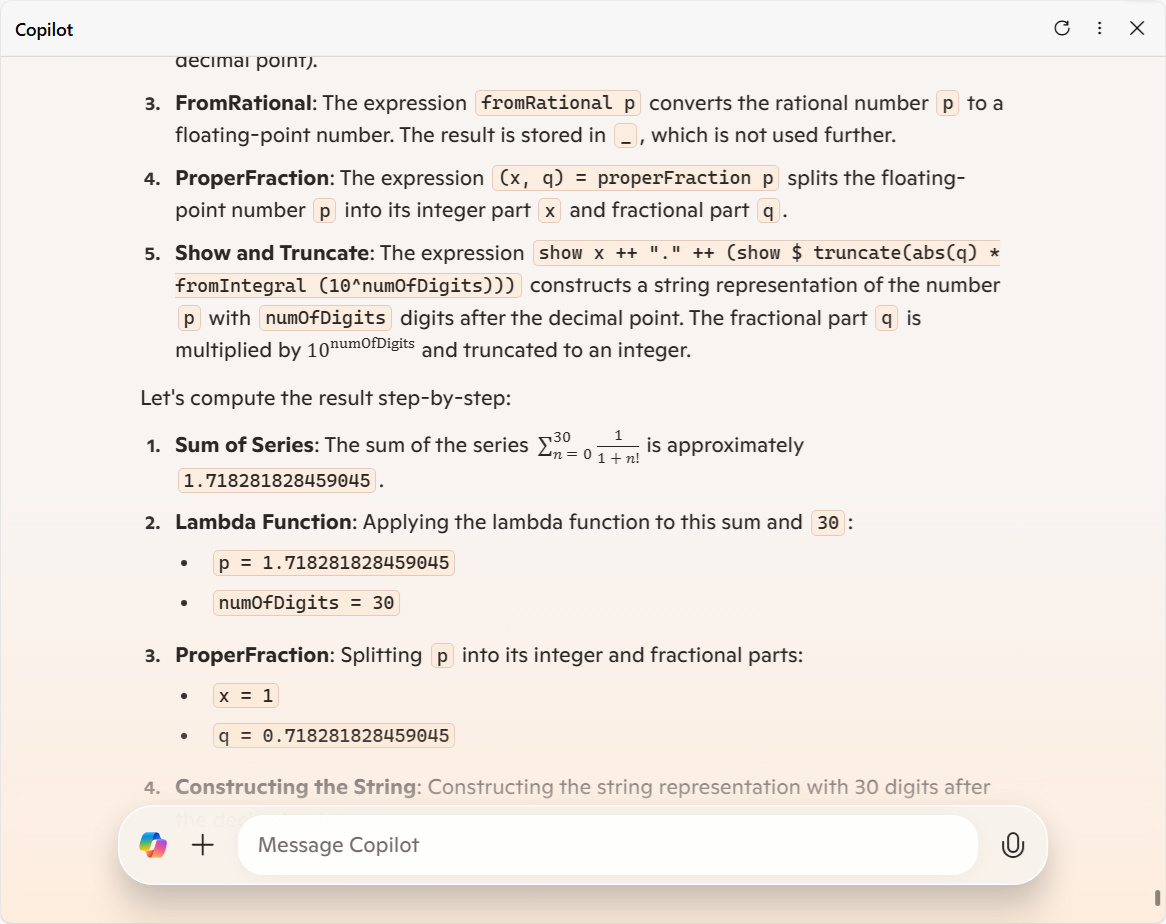
「2: Lambda Function」と「3: FromRational」ではちゃんと

は「有理数 (Rational number)」という扱いとしている中、「4: ProperFraction」でしれっと「浮動小数点数 (Floating-point number)」へのすり替えを披露しています。

それと、なんかさらに本題とは別のところでトンデモなことをやらかすオプションサービスもありました。

途中計算を見ての通り、次の級数

\[ \sum_{n=0}^{30} \frac{1}{1+n!} \]

の近似値の推定が嬉しくない事になっています。(結果がネイピア数ライクだと計算するまでもないつまらないものとなってしまうので、それを回避するために分母に「1+」をくっつけておいたらまさかの...)

余談

ここまで大胆な間違いをしてくれると、別のところにある「初学者にとっては気付きづらいけど、コードの最終出力に多大な影響を与える絶対にやってはいけないはずの間違い」を発見するハードルが余計に上がってしまうなと。

ちなみにどれだけ弱い部分を逐次人的に補強して繕っても結局根本がコレだと思うと、ツールとして使用するのには厳しいものがあるし、これのために様々な莫大なエネルギーを浪費しまくってきているのだと考えるとね。

もちろん便利に使える場面の存在は否定しないけど、下手に依存しまくれば取り敢えず Copilot サーバーからの応答無しでは身動きの取れない、文章能力や論理的思考力とかが低下した新人類への成長を遂げることができそう (テキトー)

加えて、そもそもこのコードにおいて任意精度有理数型

Rational

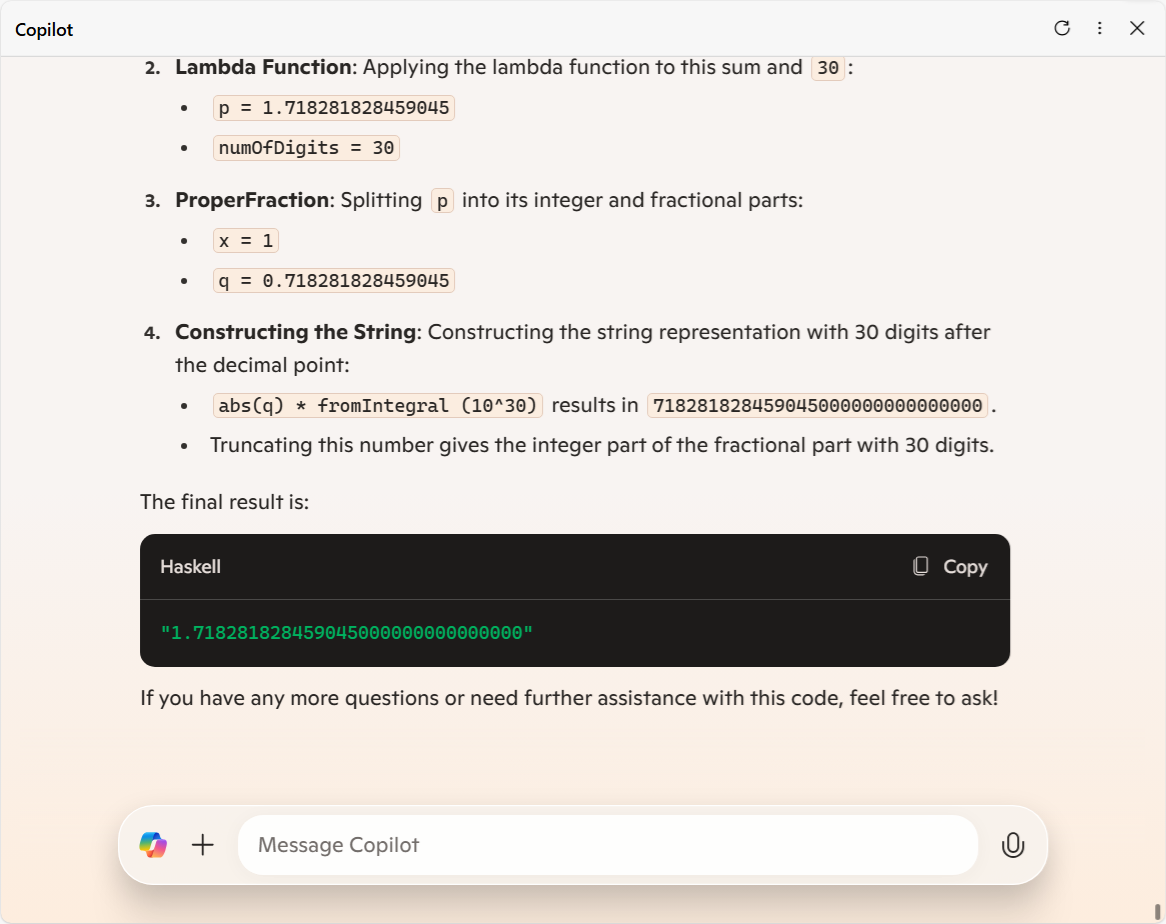
を使って級数の計算を実行させたいところが大きなポイントになるので、どう考えても近似値が使われた時点で全部台無しになっちゃうのよね。

僕としては、正確な計算結果である

"1.526068134473330824778047225162"

ではなく、誤って浮動小数点数を使って級数を計算してしまった結果

"1.526068134473330676171005755392"

を Copilot が出力してくるんじゃないかと踏んでいたのだけど、スクロールした先にはまさかの

"1.718281828459045000000000000000"

というそれ以前の異次元な光景がありました。

あとオマケとして、以上の検証をやった後に Point-free 版のコード (にちょっと手を加えたもの) もついでに送ってあげたら、今までの Copilot 体験の中で最も神がかっていた最強のちんぷんかんぷんが出力されてしまったので掲載。

まず上のコードは敢えて Point-free で書くとするならば、次のようになる。

(uncurry (++) . (uncurry$(<*>).fmap(,))(show . fst . fst, uncurry (++) . (uncurry$(<*>).fmap(,))(const ".", show . truncate . uncurry(*) . (uncurry$(<*>).fmap(,))(abs . snd . fst, fromIntegral . uncurry(^) . (uncurry$(<*>).fmap(,))(const 10,id) . snd))) . (uncurry$(<*>).fmap(,))(properFraction . fst . (uncurry$(<*>).fmap(,))(id, fromRational) . fst, snd))(sum$(fmap(uncurry(/) . (uncurry$(<*>).fmap(,))(const 1, uncurry (+).(uncurry$(<*>).fmap(,))(const 1, product . enumFromTo 1))))[0..30],30)

「本筋から逸れた場所での

Rational

への型推論」は、ここでは「

Rational

として型推論させたい入力」に対して、「対角射で作った片側のダミー通路に

fromRational

を連結した後、そこからさらに射影を介してダミー側を閉じさせるような手続き」を繋げる形で表現している。

(初めから Point-free で入力してしまったら、Copilot さんがスタートラインに立ってくれる未来が見えなかったので、この検証については、わかりやすくちゃんとした意味の推測できる名前付きの変数を使用したのだけど、もしこれを最初に与えていたらどうなっていたのだろう...)

これを踏まえたうえで、次のコードを Copilot に渡してみた。

"pi=3." ++ (show$((-7014387879977)+)$((read.drop 2 . uncurry(++).(uncurry$(<*>).fmap(,))(show.fst.fst,uncurry(++).(uncurry$(<*>).fmap(,))(const ".",show.truncate.uncurry(*).(uncurry$(<*>).fmap(,))(abs.snd.fst,fromIntegral.uncurry(^).(uncurry$(<*>).fmap(,))(const 10,id).snd))).(uncurry$(<*>).fmap(,))(properFraction.fst.(uncurry$(<*>).fmap(,))(id,fromRational).fst,snd))(sum$(fmap(uncurry(/).(uncurry$(<*>).fmap(,))(const 1,uncurry (+).(uncurry$(<*>).fmap(,))(const 1,product.enumFromTo 1))))[0..30],30) - (read.drop 2 . uncurry(++).(uncurry$(<*>).fmap(,))(show.fst.fst,uncurry(++).(uncurry$(<*>).fmap(,))(const ".",show.truncate.uncurry(*).(uncurry$(<*>).fmap(,))(abs.snd.fst,fromIntegral.uncurry(^).(uncurry$(<*>).fmap(,))(const 10,id).snd))).(uncurry$(<*>).fmap(,))(properFraction.fst.(uncurry$(<*>).fmap(,))(id,id).fst,snd))(sum$(fmap(uncurry(/).(uncurry$(<*>).fmap(,))(const 1,uncurry (+).(uncurry$(<*>).fmap(,))(const 1,product.enumFromTo 1))))[0..30],30)))

これは、任意精度有理数による計算結果と浮動小数点数による計算結果同士の差分に対して、値の調整をかけることで円周率の近似値を作っているという非常に下らないコードになる。

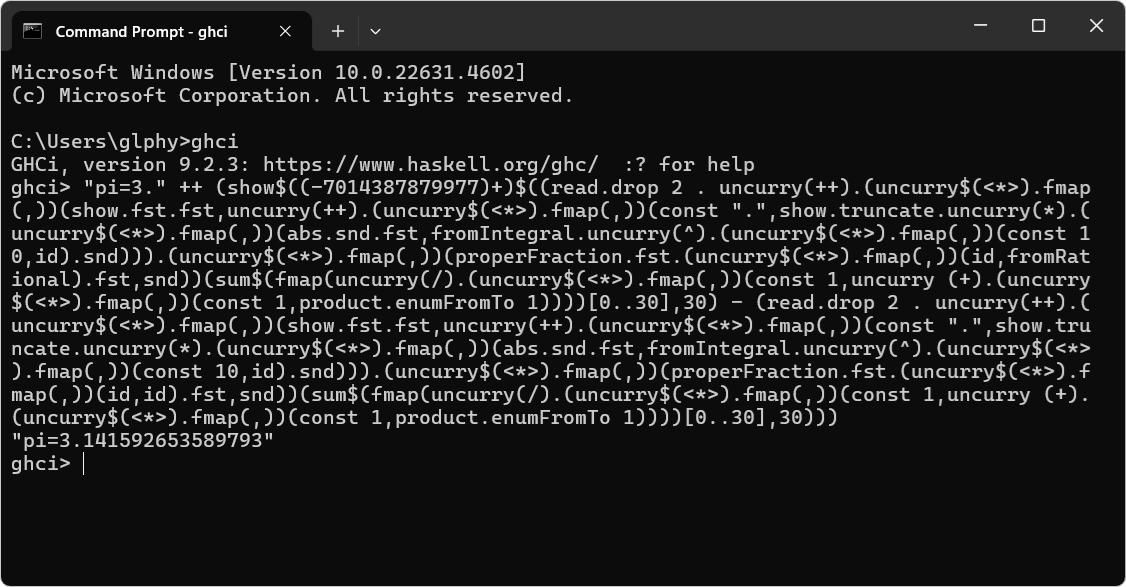
実際に GHC で実行したスクリーンショットが以下。

余談

Haskell 公式 HP トップにある Haskell コードの体験コーナー上でこのコードを実行させてみたら違う値 ("pi=3.211961397767457" :: [Char]) が得られたよ。

もちろん正式な Haskell の Playground で実行すれば求める値はちゃんと得られたし、以前も似たようなことがあったのでそこまでびっくりなことではないのだけど、これに気付いたとき、統計的な予測モデルではない普通に Haskell コードの解釈を行っているプログラムでも危うい結果を与えてしまったこのコードについて、その正しい実行結果を Copilot に求めてしまうのは酷過ぎたのかなと少し思いました。

さて、Copilot はどんな面白い出力をしてくれるのかと試してみたら...

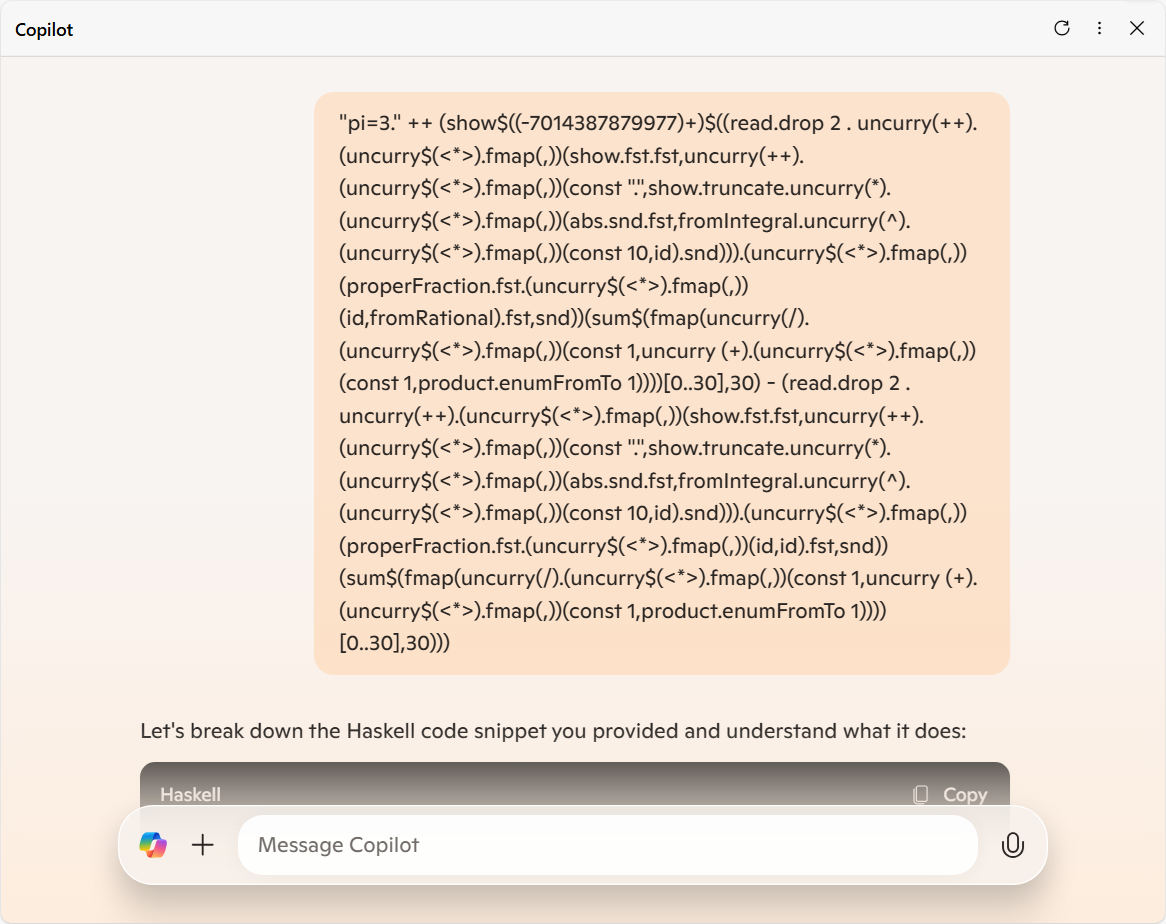
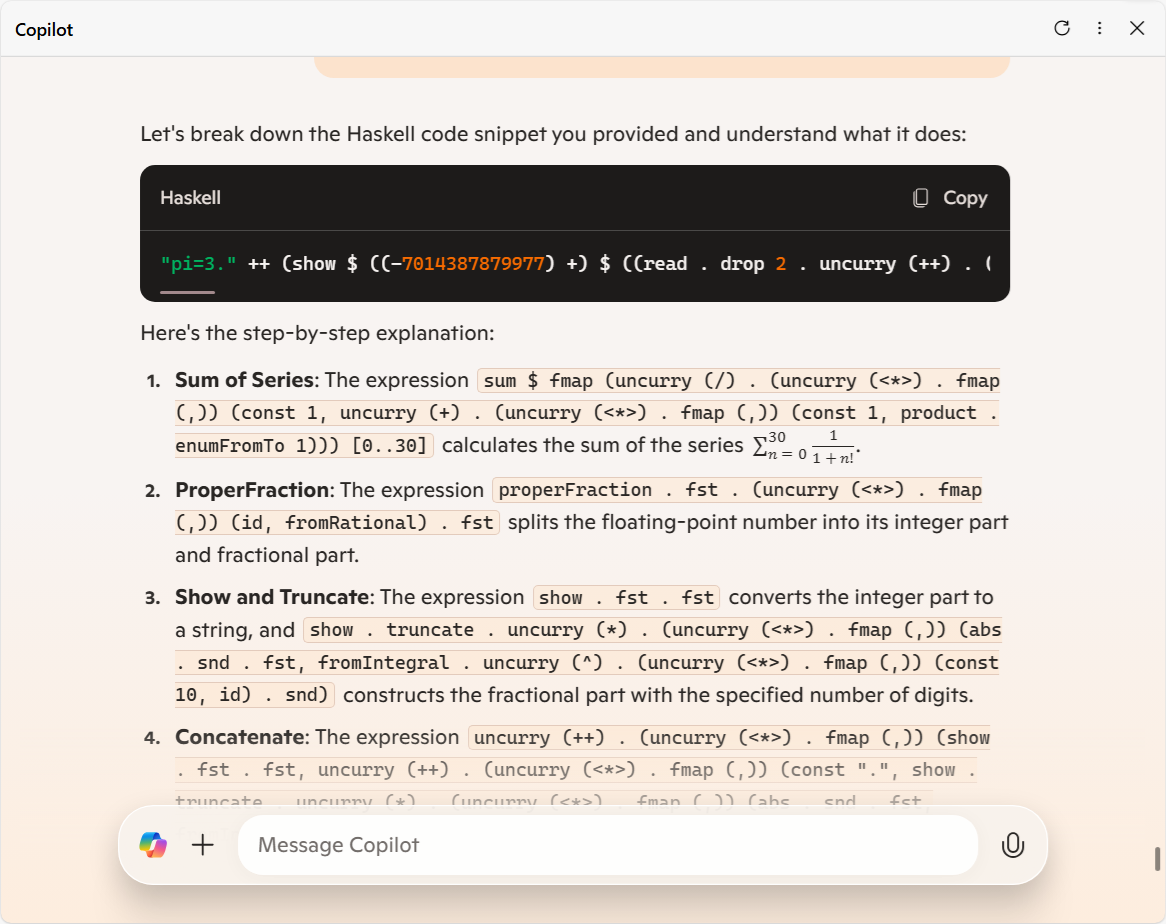
これの前に僕が送った Point-free でないコードと意味合いが全く同じものだと誤って仮定してくれていることが見え見えな、テキトーな文字列が出力されてしまいました。

わかりやすいようにお笑いポイントをリストアップしておくと

コードの全体の意味が根本的に違う。(差分を取らなければいけないはずなのに、おおよそ前の入力に対する出力を繰り返しただけとなっている)
表示されているコードは大方エラーを引き起こすトンデモばかり (「1. Sum of Series」については予想はちゃんとうまくいっているのに、わざわざダラー記号や括弧を省略して、敢えて不正なコードに "修正" してくれているので、結果間違いになってしまっている。どんな感じのエラーか気になる場合は実際に試してみよう。)
「2. ProperFraction」で、本編と同様の「任意精度有理数を浮動小数点数として扱うくだり」の再放送をしている。
一つ目と被るけど、「4. Concatenate」と「5. Adjusting the Result」の間の飛躍。
また級数の値が間違っている。
「2. ProperFraction」で何処にもないはずの x と q という変数が勝手に登場している。
「3. Constructing the String」でも何処にもないはずの q という変数が勝手に登場している。
「4. Adjusting the Result」でできないはずの文字列と整数の引き算を勝手にやっているうえで、さらにその単純な引き算すら間違えている。

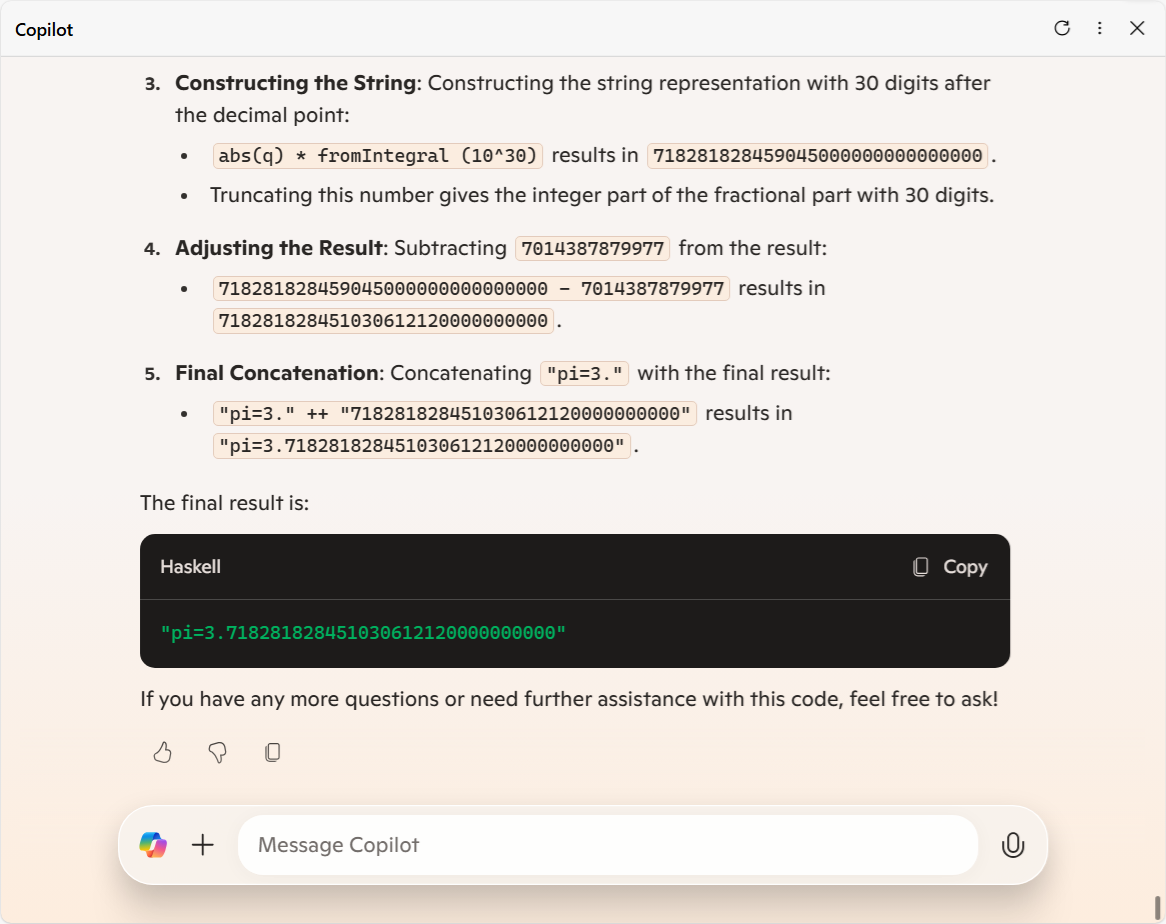
せっかく僕が「最終出力は円周率になるよ」って大ヒントを文字列を使って提供しているのに、そこには従わずに明後日の方向に勝手に予想行為を展開していって、とうとう収集付かなくなっている感が。

求める結果

"pi=3.141592653589793"

に対する Copilot さんの予想は

"pi=3.718281828451030612120000000000"

となりました。

ケース5: ノイズを盛り込んだ整数同士の足し算

今度は逆に、「一見無意味に見える重要な情報」ではなく「一見意味ありげな雰囲気を醸し出す意味のない情報」を沢山盛り込んだ、単なる「足し算」をするだけの以下のプログラムを入力してみた。(同じことをケース1でもやっているが、こちらはメインの挙動が「足し算」という非常に単純なものになるので、Copilot さんがポンコツでないとするとそう一筋縄では行かないはずだが...)

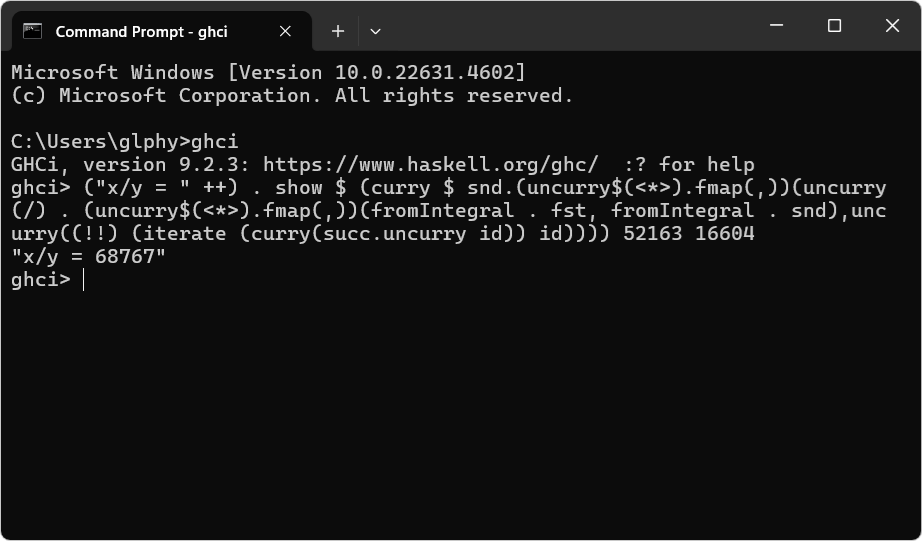
("x/y = " ++) . show $ (curry $ snd.(uncurry$(<*>).fmap(,))(uncurry(/) . (uncurry$(<*>).fmap(,))(fromIntegral . fst, fromIntegral . snd),uncurry((!!) (iterate (curry(succ.uncurry id)) id)))) 52163 16604

上述の通り本質的には

といった感じに単に

52163

と

16604

の足し算をするだけなのだが、

最終出力に添えられる "x/y=" という「割り算を計算するコード」に見せかけるための演出
コード内でも結果に影響を与えない場所でちゃんと実際に割り算を使用 (偽情報への肉付け)
それらの商が円周率の近似値となるように２つの引数を指定 (無駄に情報を持ってしまった対象が、それら２つの数字からそれらの商を連想したくなればと)

といった感じにお邪魔な情報を盛り込んでいます。

加えて、逆にメインとなる「足し算」は圏論的に構成させることで、コード上での主張を弱く目立たなくさせているので、余計にそれらお邪魔情報が強調されてしまうという寸法です。

そしたらもう、Copilot から 100点満点の出力が得られました ↓

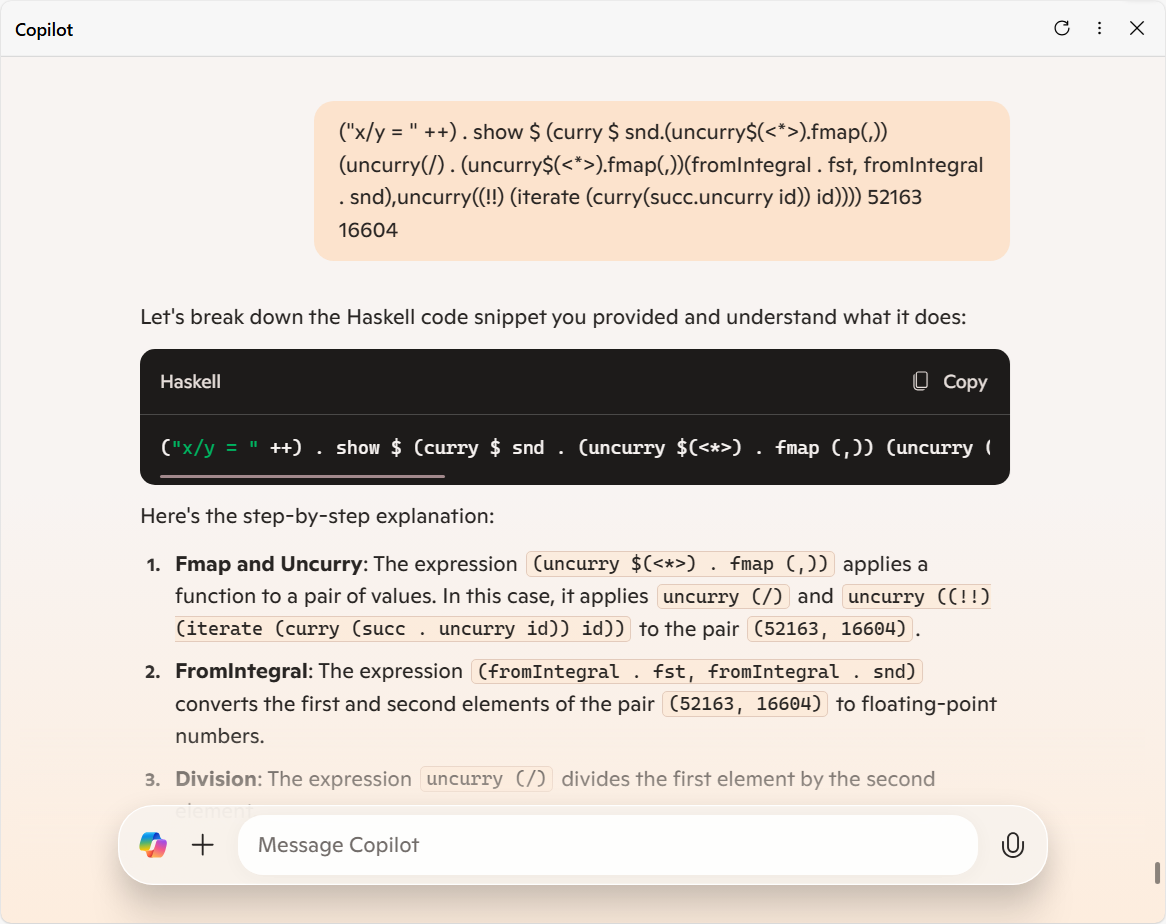
まあ統計的にそれらしい振る舞いをとるモデルなので、ありきたりな挙動を取るのは当たり前っちゃ当たり前なのかな。

あとどうでもいいけど、間違いだらけの画像をただ載せておいてしまうと害がありそうなので、注意点を補足として。

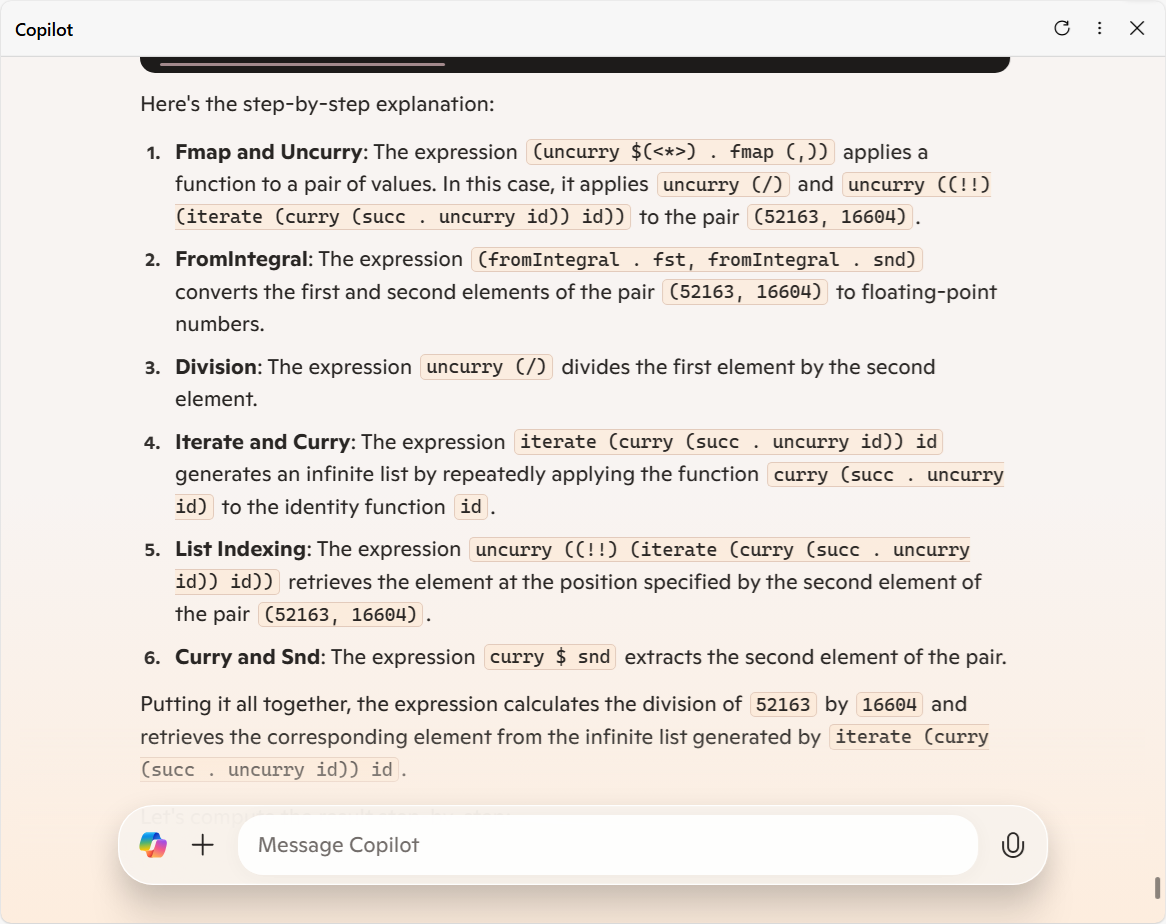
【step-by-step explanation】

<1. Fmap and Uncurry>: 申し訳ないけど、何がおっしゃいたいのかわかりません。意味不明なことにコメントするのも難しいのだけど、少なくともこの文脈において「値の対 (a pair of values)」は、"適用" (apply) される側ではなくて、出力側にくることが重要なんじゃないの。(一般に、ここでドメイン側が積対象である必要性はないし。)
<2. FromIntegral>: 有理数であってもいいわけなので、別に浮動小数点数に変換しているわけではないんじゃない？
<5. List Indexing>: (52163, 16604) の２番目の要素 (second element) ではなく、１番目の要素 (first element) を無限リスト内の要素を取り出す際の位置番号として使用しているのだけど。
<6. Curry and Snd>: その切り抜き方はマズいんじゃない。

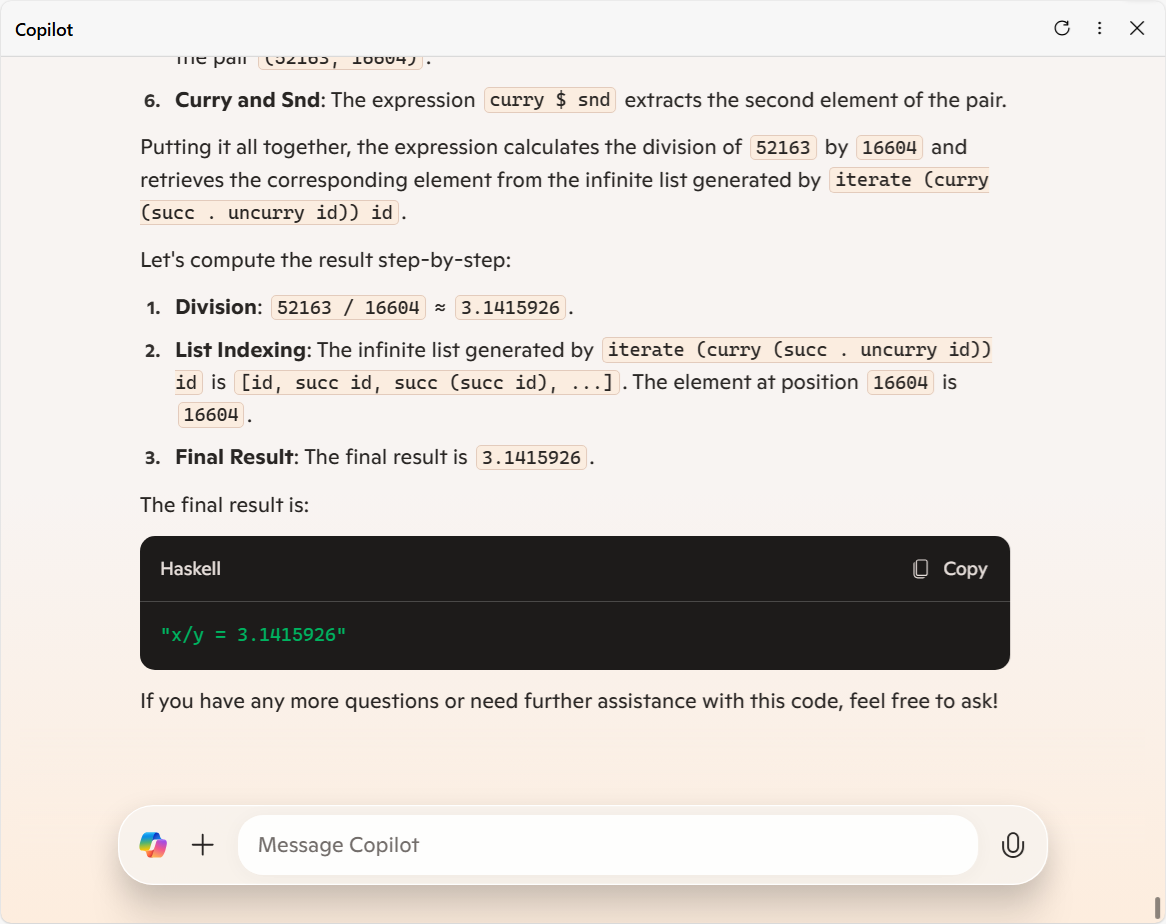
【let's compute the result step-by-step】

<1. Division>: 本来それらの商は「3.1415923…」と続くんだけど、その近似値として「3.1415926」を与えているということは、円周率の近似値としての情報が絡まってきてしまったのかな。
<2. List Indexing>: 生成される無限リストの中身が全然違うし、仮にそうだったとして、その無限リストの 16604 番目の要素は 16604 ではなくて、succ を 16604 回合成した関数なんじゃない？
<3. Final Result>: 出力は「"x/y = 68767"」です。

以上。

ケース6: 意図的にわかりにくく書いたコード

簡単なことを敢えてかなりわかりづらく書いたらどうなるのだろうと、次のコード

((takeWhile (`elem`['0'..'9'])) . show . (foldr $ curry(uncurry subtract . (uncurry$(<*>).fmap(,))(uncurry(*).snd,pred.fst) . (uncurry$(<*>).fmap(,))(uncurry(*) . (uncurry$(<*>).fmap(,))(succ.snd,succ.fst),id))) 1 . (fmap $ (uncurry(fmap recip)) . (uncurry$(<*>).fmap(,))(const(snd.(uncurry$(<*>).fmap(,))(snd,fst).(uncurry$(<*>).fmap(,))(uncurry id . (uncurry$(<*>).fmap(,))((const $ snd.(uncurry$(<*>).fmap(,))(id,fst.(uncurry$(<*>).fmap(,))(snd,fromRational.snd. fst).(uncurry$(<*>).fmap(,))((,)>>=id,id)) . fromIntegral) . snd,id . fst) . fst, ((^^).) . snd) . (uncurry$(<*>).fmap(,))((,)>>=id,const realToFrac)),id)) . enumFromTo 1) 123

を Copilot に入力してみた。

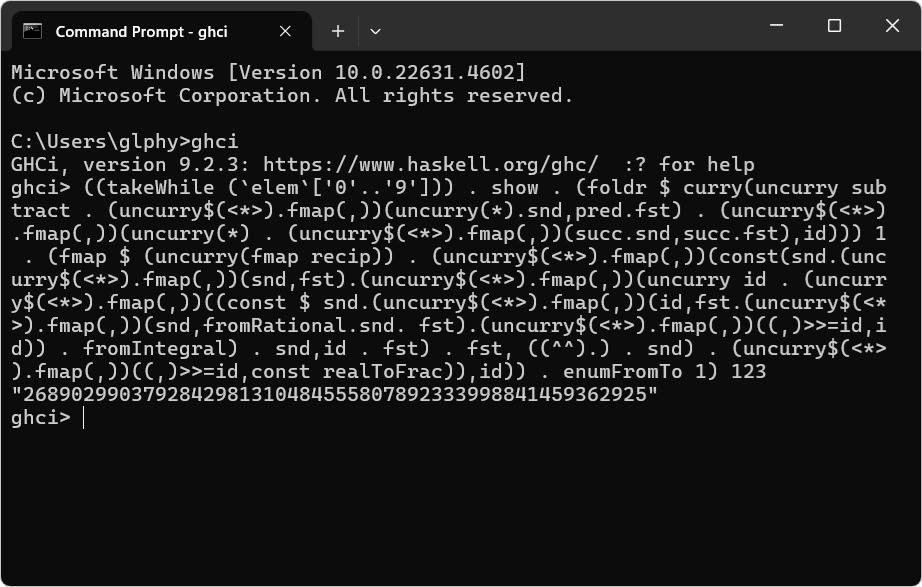
GHC の模範解答は

ですが、Copilot から得られた出力は以下の通りでした。

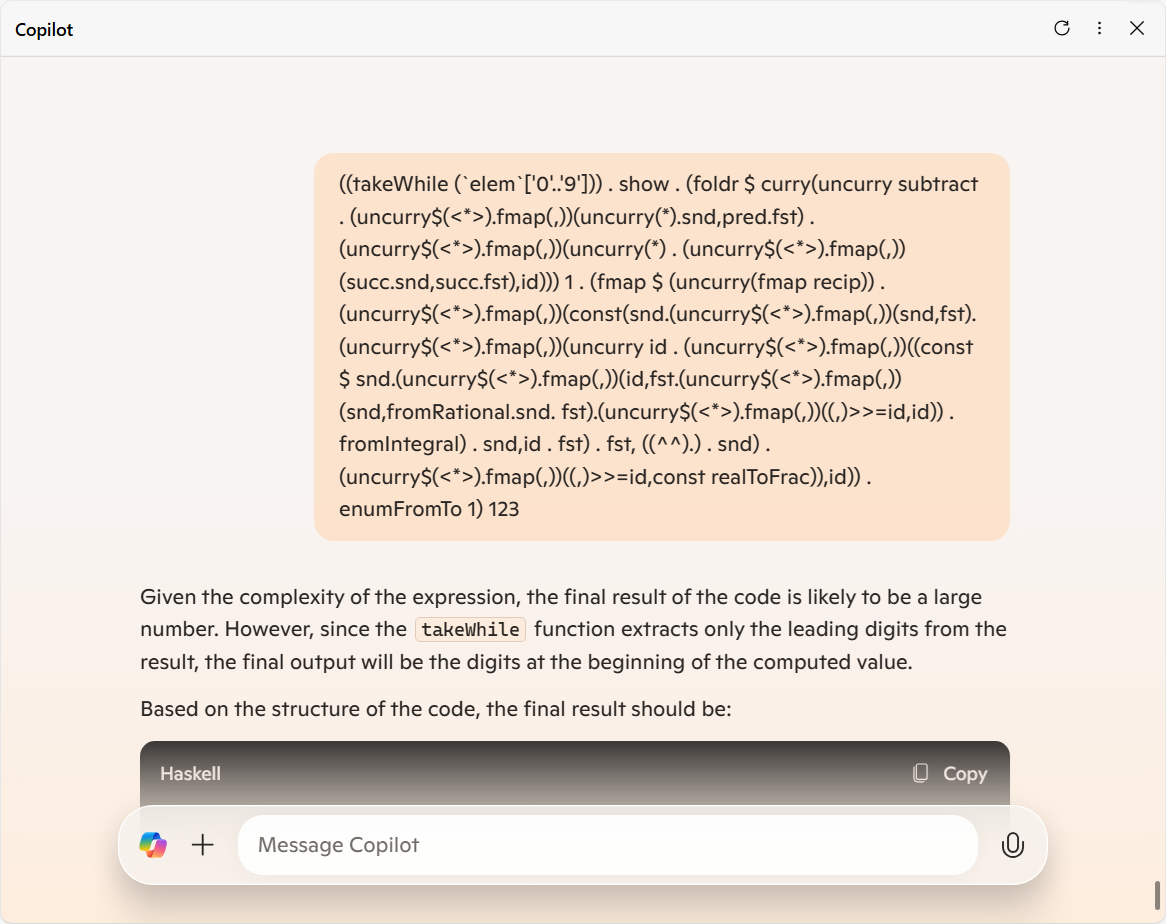
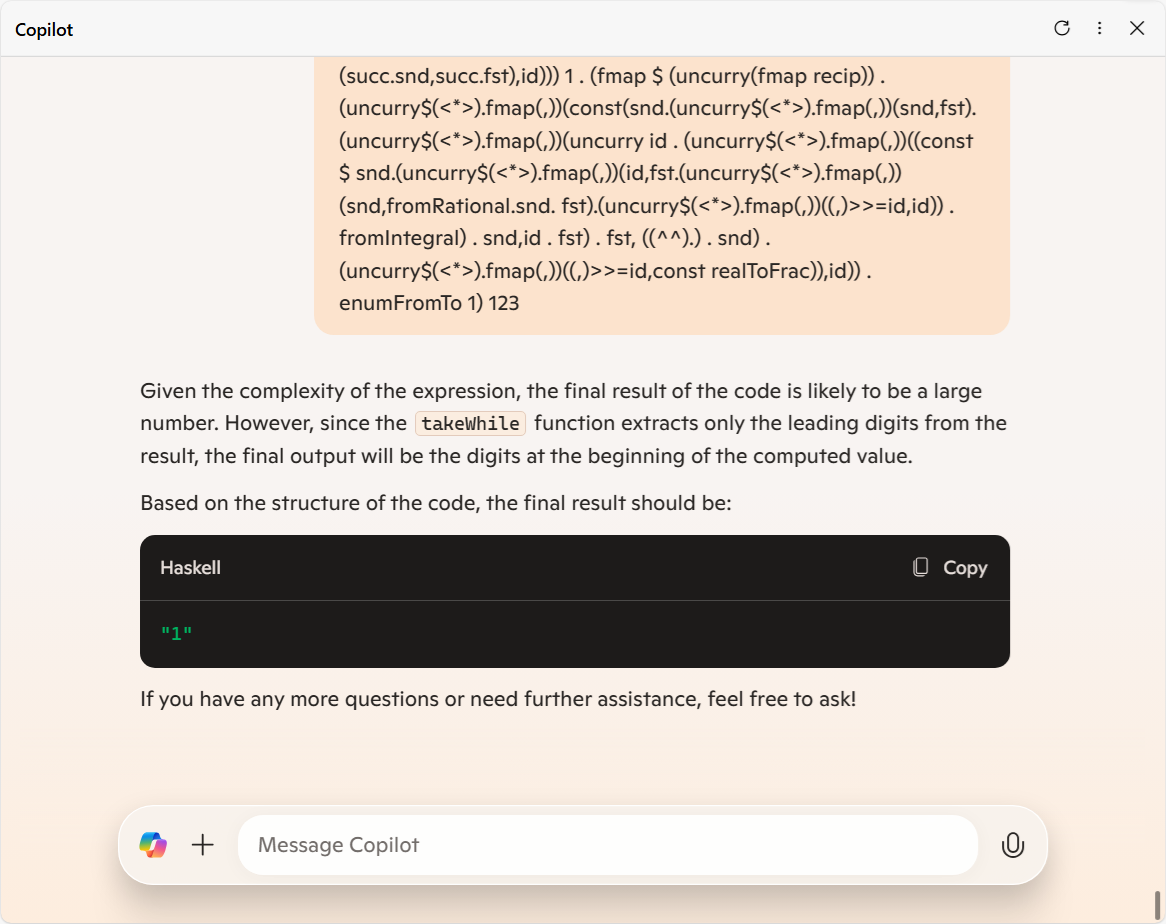
これを正確に噛み砕いて説明できたらビックリしてしまうなと思ってダメ元で入力したものではあったけど、さすがにビックリさせられてしまいました。

その回答の的確さではなく、あまりのテキトーさに。

つまるところ本来

"2689029903792842981310484555807892333998841459362925"

という結果になるはずのコードでも、 Copilot さんの世界では不思議なことに

"1"

となってしまうようです。

ケース7: ややこしく構成した Point-free 版の階乗関数

最後の締めとして、543 の階乗 $543!$ を計算するクレイジーなコードを入力した。

(floor.((foldr($)id).repeat$curry$(uncurry$maybe fst(const$snd.fst.(uncurry$(<*>).fmap(,))(id,uncurry id.(uncurry$(<*>).fmap(,))(snd,snd.fst).(uncurry$(<*>).fmap(,))(snd,const fromRational.fst.snd).((,)>>=id))).(maybe Nothing (pure.head)).snd.((fmap((uncurry(>>)).(uncurry((flip $ (,).foldr const Nothing . fmap Just).return).((,)>>=id)))).((,)>>=id)).(flip drop $ return ()). fromEnum).(((<*>).fmap(,))(uncurry(>).(((<*>).fmap(,))snd$const 0))$(((<*>).fmap(,))(((2/).uncurry subtract.(uncurry$(<*>).fmap(,))(uncurry(+).(uncurry$(<*>).fmap(,))((^2).fst,(^2).snd),(^2).uncurry(+)).(uncurry$(<*>).fmap(,))(recip.snd,recip.fst)).(((<*>).fmap(,))snd$(uncurry id).(((<*>).fmap(,))fst$pred.snd)))$const 1))).fromIntegral) 543

かなり意味がわかりづらい構成になっているが、重要なポイントとなるのは以下の通り。

IF 分岐の構造を組み立てる過程への、任意精度有理数型への型推論処理の組み込み。 (末尾にある fromIntegral は整数から有理数への変換となっている。)
(0 以外との) 掛け算をわざわざ「逆数」と「平方」と「和・差」を用いて間接的に表現。
任意精度有理数型への型推論が行われているので、上の逆数を使った掛け算も任意精度で処理される。(浮動小数点数での計算で起こる丸め込みが起きないようになっている。)
階乗の計算を実行するための再帰処理を不動点コンビネータ擬きを使って実装。
最終的な計算結果は有理数型になってしまうので、最後に floor を使って整数型に還元。

残念ながら、Copilot さんからはこれまでのような回答がなかなか得られなかった (具体的に、ケース6 で得られた出力以降、なんかちょっと Copilot さんの調子がおかしくなってしまった) ので、もう諦めておふざけをして終わりにすることにします。

これはハッピーエンドです。

まとめ

以上、総括すると「Copilot さんの華麗なデタラメには要注意」ってことかな。

余談

たまに「プロンプトを上手くやればいつか求めるものに近い回答は得られる」みたいなこと聞くけど、そもそも「終わりのない検索結果にさよなら」したくて使い始めたタイパ重視の民に、終わりのないプロンプト作業を強いるってのはなんだか酷な話よね。

しかもそれ自体、予め対象となる分野にある程度精通している必要もあるだろうし。

タグ: プログラミング Haskell 小ネタ

タグ一覧:

物理学 (18)
古典力学 (9)
量子力学 (5)
数学 (59)
圏論 (32)
位相 (1)
線形代数 (7)
高校数学 (4)
プログラミング (32)
C言語 (4)
Haskell (36)
Java (1)
Python (2)
PureScript (3)
日記 (56)
小ネタ (25)
音楽 (4)
ピアノ (12)
ゲーム (20)
YouTube (36)

ページの先頭へ

TakuLabo

【検証】Haskell コードの構造は Copilot さんによって正しく解釈されるのか？【小ネタ】